Codeforces #286 Div 1 简要题解
A. Mr. Kitayuta, the Treasure Hunter
题目链接
http://codeforces.com/contest/506/problem/A
题目大意
有 n 个岛屿,分别标号为 0 到 30000 ,某些岛屿上有宝藏,初始时你在起点0,你的跳跃距离为 d 。假如你当前在岛屿 i 上,跳跃距离为 di ,那么你可以在跳到岛屿 i+di 后选择下一次你的跳跃距离为 di−1 或 di 或 di+1 ,但是任何时刻跳跃距离都必须为正整数。问你在这个游戏里最多能拿到多少宝藏
思路
很显然我们可以得到一个DP的思路:
用 f[i][j] 来表示当前在岛屿 i 上,当前的跳跃距离为 j 。那么可以得到DP方程:
在DP过程中,我们实时维护最终的答案,也就是 f[][] 数组里的最大值。
但是j的范围可能非常大,因此无论是在空间还是时间上,上述的做法显然是不可行的。
但是考虑最极端的情况:
在最极端的 d=0 时, t=244 ,因此如果我们用 j−d 来代替 j 作为状态来表示的话,这一维的状态数目大大减少为百位数级别,考虑到 j−d 可能小于0,因此我们最终采用 j−d+300 来作为第二维状态,避免出现负数
代码
#include B. Mr. Kitayuta’s Technology
题目链接
http://codeforces.com/contest/506/problem/B
题目大意
给出 n 个点以及 m 个限制要求,每个要求是让点 ai 能走到点 bi ,问最少给这个图加入多少条边,才能满足所有的要求
思路
首先把所有的要求看成有向边 ai−>bi 加入到图中,假如我们把所有的有向边看成无向边的话,对于每个大小为 t 的弱连通分量(在无向图中相互可达的联通块),若在原图中,这个联通块中包含一个有向环的话,显然我们在这个弱连通分量里只需要加入 t 条边即可满足所有的需求(即构造边数为 t 的强连通分量),而不存在这样的有向环的话,我们一定能通过拓扑排序找出一个长度为 t 的序列,将序列里的点从左到右依次连边即可满足输入数据的要求,这样只需要 t−1 条边即可满足要求。
因此我们首先通过DFS/BFS找出所有的弱连通分量,然后对于每个弱连通分量做拓扑排序判环即可得到答案。
代码
#include int u=q[h++];
for(int p=head_dir[u];p!=-1;p=edges_dir[p].next)
{
int v=edges_dir[p].v;
inDegree[v]--;
if(!inDegree[v])
{
tot++;
q[t++]=v;
}
}
}
return tot!=top;
}
int main()
{
memset(head_dir,-1,sizeof(head_dir));
memset(head_undir,-1,sizeof(head_undir));
int ans=0;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int u,v;
scanf("%d%d",&u,&v);
AddEdge_dir(u,v);
AddEdge_undir(u,v);
}
for(int i=1;i<=n;i++)
{
if(vis[i]) continue;
top=0;
FindWCC(i,-1);
if(FindCir()) ans+=top;
else ans+=top-1;
}
printf("%d\n",ans);
return 0;
}
C. Mr. Kitayuta vs. Bamboos
题目链接
http://codeforces.com/contest/506/problem/C
题目大意
给你 n 个竹子,以及每个竹子初始的高度 hi ,每天白天你可以选择对其中不超过K个竹子选择将其的高度减少P(若某个竹子高度 <P ,则减少高度后那个竹子高度变为0),每天晚上每个竹子i都会长高高度a[i],问 m 天后最高的那个竹子的高度最小值
思路
显然直接求值比较困难,需要二分答案 maxh (最后最高的那个竹子高度不超过 maxh )。问题变成判定性问题,最后最高的那个竹子高度是否可以不超过 maxh 。正着做比较麻烦,因为要考虑到砍伐一次竹子后竹子高度变为0的特殊情况,考虑倒着做,即初始时每个竹子高度均为 maxh ,每天晚上每个竹子会减少高度 ai ,每天白天你可以选择对其中不超过K个竹子选择将其的高度增加P,并且保证任何时刻任何竹子高度均大于等于0,问 m 天后是否可以让每个竹子高度均大于等于 hi 。
证明倒着推的正确性:只有在 m 天后每个竹子高度均大于等于 hi ,才能让所有的竹子按照原来正向的顺序,以和倒着做相同的操作反过来让每个竹子最终的高度小于等于 maxh ,见下图,绿色线代表倒着推的话一根竹子的每天生长情况,蓝色线代表正着推的话一根竹子的每天生长情况(来自Codeforces官方题解)
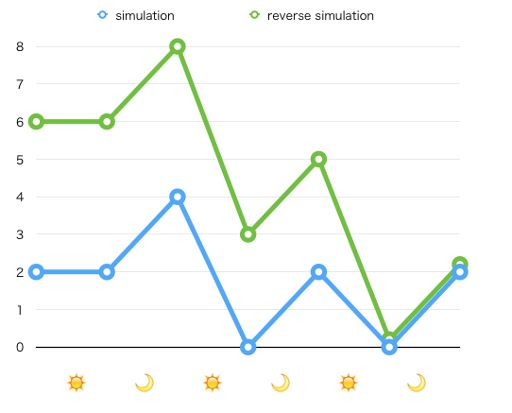
可以发现如果每天对这个竹子的操作相同的话,要想让最后的这个竹子的高度和倒着推的高度一样,之前每天正着推的高度都必须小于等于倒着推的高度。
下面我们就需要通过倒着贪心来判断结果。首先我们尽量少砍伐(倒着推应该叫拔高?)竹子,保证每根竹子倒回来的初始高度大于等于0,且每天每根竹子的高度均大于等于0,我们可以维护一个小根堆,堆里保存的是每根竹子的高度在自然生长下需要多长时间就会变成负数。每天我们取堆里前 K 小的竹子,将它们拔高处理,若存在某一天来不及拔高竹子(存在某个竹子的高度在这一天之前就变为0了),就可以立刻判定 m 天后不能可以让每个竹子高度均大于等于 hi 。
现在我们让所有竹子倒过来生长,最终每个竹子高度均大于等于0后,就需要让每个竹子的高度拔高,使得它们最终高度大于等于 hi ,显然此时由于在生长过程中,每个竹子在任意时刻高度均大于等于0,故此时补充的操作无论是在何时发生都是一样的。这时直接通过数学方法,计算每个竹子和 hi 之间相差的高度以考虑需要补上多少次操作就够了。
这种做法非常巧妙,但是只适用于判定性问题,并不能直接求值
代码
#include vector,greater >heap;
bool check(LL lastMaxH)
{
while(!heap.empty()) heap.pop(); //!!!!
for(int i=1;i<=n;i++) nowh[i]=lastMaxH;
for(int i=1;i<=n;i++)
{
if(nowh[i]-m*a[i]>=0) continue;
heap.push(make_pair(nowh[i]/a[i]-1,i));
}
int tot=0; //最后tot=使得所有竹子的高度大于等于初始高度的最少进行的砍伐次数
for(;tot<=m*K;tot++) //进行tot次砍竹(倒着处理就是增加高度)操作,第tot次操作发生在tot/K天,这个循环后使得每个竹子在开始的那天高度不为负数
{
if(heap.empty()) break;
pr now=heap.top();
heap.pop();
if(now.firstreturn false;
nowh[now.second]+=P;
if(nowh[now.second]-m*a[now.second]>=0) continue;
heap.push(make_pair(nowh[now.second]/a[now.second]-1,now.second));
}
if(tot>m*K) return false;
for(int i=1;i<=n;i++)
{
if(nowh[i]-m*a[i]>=h[i]) continue;
tot+=((h[i]-nowh[i]+m*a[i])+P-1)/P; //加上一定操作次数,使得第i个竹子刚刚好比它的初始高度h[i]高
if(tot>m*K) return false;
}
return true;
}
int main()
{
scanf("%d%d%d%I64d",&n,&m,&K,&P);
for(int i=1;i<=n;i++)
scanf("%I64d%I64d",&h[i],&a[i]);
LL lowerBound=0,upperBound=1e15,ans=-1;
while(lowerBound<=upperBound)
{
LL mid=(lowerBound+upperBound)>>1;
if(check(mid))
{
ans=mid;
upperBound=mid-1;
}
else lowerBound=mid+1;
}
printf("%I64d\n",ans);
return 0;
}
D. Mr. Kitayuta’s Colorful Graph
题目链接
http://codeforces.com/contest/506/problem/D
题目大意
给你一个 n 个点 m 条边的无向图,图中每条边都有颜色(数字表示),多次询问从一个点 a 到另一点 b 有多少条纯色的路径
思路
很显然,若对于 t 种颜色中的每种颜色 coli ,在只包含颜色 coli 的无向边的图里, a 和 b 都是联通的,那么它们之间纯色路径的个数就是 t 。
因此我们可以先对所有边按照颜色进行离线排序,对于每种颜色的无向边分开考虑,用并查集维护只含该种颜色的边的无向图的连通性,然后离线回答所有的询问的答案,看有多少个询问的 a 和 b 点是在这种颜色的无向图里联通,就把这些询问的答案+1。
问题是离线回答答案时,若是扫描询问来回答答案, q≤105 ,可能TLE,而若是枚举点对来回答答案, n≤105 ,也可能TLE。这里我参考了其他人的优化方法: n≤100 时就枚举点对回答答案, n>100 时就扫描询问来回答答案。这样做就不会TLE了
当然还有地方需要优化:每次做并查集数组和其他数组初始化时,我们只初始化那些被修改过的地方,数组里的其他地方不需要优化,不然前面的优化就白做了,还是会TLE
代码
#include int ,int>,int>mp;
vector<int>vec[MAXV],block;
bool inBlock[MAXV];
int n,m,q;
struct edge
{
int u,v,col;
}edges[MAXE];
bool cmp(edge a,edge b)
{
return a.colint f[MAXV];
int findSet(int x)
{
if(f[x]==x) return x;
return f[x]=findSet(f[x]);
}
void set_init()
{
for(int i=0;ifalse;
}
}
struct Query
{
int x,y;
}query[MAXV];
int L,R;
void calc()
{
if(block.size()>100) //扫一遍所有的点,并遍历每个点a对应的询问里的另一个点b
{
for(int i=0;iint u=block[i];
for(int j=0;jint v=vec[u][j];
int rootu=findSet(u),rootv=findSet(v);
if(rootu!=rootv) continue;
mp[make_pair(u,v)]++;
}
}
}
else //暴力枚举点对
{
for(int i=0;iint u=block[i];
for(int j=i-1;j>=0;j--)
{
int v=block[j];
int rootu=findSet(u),rootv=findSet(v);
if(rootu!=rootv) continue;
mp[make_pair(min(u,v),max(u,v))]++;
}
}
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
scanf("%d%d%d",&edges[i].u,&edges[i].v,&edges[i].col);
sort(edges+1,edges+m+1,cmp);
scanf("%d",&q);
for(int i=1;i<=q;i++)
{
int u,v;
scanf("%d%d",&u,&v);
if(u>v) swap(u,v);
query[i].x=u,query[i].y=v;
if(mp.find(make_pair(u,v))==mp.end())
{
mp[make_pair(u,v)]=0;
vec[u].push_back(v);
vec[v].push_back(u);
}
}
for(int i=0;ifor(int nowcol=edges[1].col,i=1;i<=m;i++)
{
if(edges[i].col==nowcol)
{
int rootu=findSet(edges[i].u),rootv=findSet(edges[i].v);
if(rootu!=rootv)
f[rootu]=rootv;
if(!inBlock[edges[i].u])
{
inBlock[edges[i].u]=true;
block.push_back(edges[i].u);
}
if(!inBlock[edges[i].v])
{
inBlock[edges[i].v]=true;
block.push_back(edges[i].v);
}
}
else
{
calc();
set_init();
nowcol=edges[i].col;
block.clear();
//memset(inBlock,false,sizeof(inBlock));
int rootu=findSet(edges[i].u),rootv=findSet(edges[i].v);
if(rootu!=rootv)
f[rootu]=rootv;
if(!inBlock[edges[i].u])
{
inBlock[edges[i].u]=true;
block.push_back(edges[i].u);
}
if(!inBlock[edges[i].v])
{
inBlock[edges[i].v]=true;
block.push_back(edges[i].v);
}
}
}
if(!block.empty())
calc();
for(int i=1;i<=q;i++) printf("%d\n",mp[make_pair(query[i].x,query[i].y)]);
return 0;
}