数字图像处理——第十章（图像分割）

参考：https://blog.csdn.net/mary_0830/article/details/89597672
https://blog.csdn.net/Dujing2019/article/details/90203492

形态学图像处理中，输入的是图像，输出的是从图像中提取出来的属性，分割是该方向上的另一步骤。
分割将图像细分为构成它的子区域或物体。细分的程度取决于要解决的问题。当感兴趣的物体或区域已经被检测出来了，那就停止分割。
单色图像的分割算法通常基于灰度值的两个基本性质： 不连续性和相似性。第一种是以 灰度变换（即灰度的突变）为基础分割图像，如边缘检测；第二种是根据事先预定义的 相似性准则把图像分成相似的区域，如阈值分割、区域生长、区域分裂和聚合。

图像分割的数学描述
令R表示一幅图像占据的整个空间区域。将图像分割视为把R分为n个子区域R₁，R₂，…，R_n的过程，满足：

(a)：分割必须是完全的，即每个像素都必须在一个区域内；
(b)：一个区域中的点以某种预定义的方式来连接（这些点必须是4连接或8连接的）；
©：各个区域必须不相交；
(d)：分割后的区域中的像素必须满足的属性（如，若R_i中的所有像素都有相同的灰度级，则Q(R_i) = TRUE），其中属性可以是灰度，颜色，纹理等；
(e)：两个邻接区域R_i和R_j在属性Q的意义上必须是不同的。

一、点、线和边缘检测

本节主要介绍以灰度局部剧烈变化（灰度不连续性)检测为基础的分割方法。
对一幅图中灰度的突变，局部变化可以用微分来检测。因为变化短促，可以用一阶微分和二阶微分描述。
数字函数的导数可用差分来定义。一维函数f(x)在点x处一阶导数的近似：

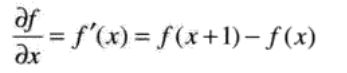
一维函数f(x)在点x处二阶导数的近似：

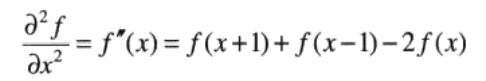
对二维图像函数f(x,y)，为表示一致性，使用偏微分，将处理沿两个空间轴的偏微分

有关一阶导数和二阶导数的结论：
(1) 一阶导数通常在图像中产生较粗的边缘；
(2) 二阶导数对精细细节，如细线、孤立点和噪声有较强的响应；
(3) 二阶导数在灰度斜坡和灰度台阶过渡处会产生双边缘响应；
(4) 二阶导数的符号可用于确定边缘的过渡是从亮到暗（负二阶导数）还是从暗到亮（正二阶导数）

计算图像中每个像素位置处的一阶导数和二阶导数的另一种方法是使用空间滤波器。
对3*3滤波器掩膜来说，导数是计算模板系数与被该模板覆盖的区域中的灰度值的乘积之和。即模板在该区域中心点处的响应如下：

z_k为像素的灰度，w_k为对应位置的系数。
其中，3 x 3的空间滤波器为：

1.1 孤立点的检测

点的检测应以二阶导数为基础。
孤立点常嵌在常数区域（或图像中亮度基本不变的区域）中，孤立点的灰度将完全不同与其周围像素。
点检测通常使用拉普拉斯算子进行检测。第三章介绍的四种拉普拉斯模板如下：

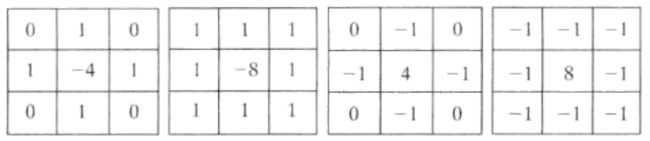
原理：如果在某个点处，该模板的响应R的绝对值超过了某个指定阈值，则说明在模板中心位置(x,y)处的该点已被检测到。输出图像中，这样的点标注为1，其他所有的点标注为0，从而产生一幅二值图像。公式描述如下：

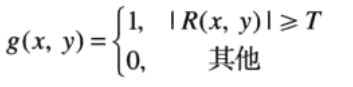
其中，g是输出图像，T为一个非负阈值。R为上述介绍过的，即模板的系数与其覆盖区域的灰度值的乘积之和，也叫作模板的响应。
当模板的中心位于一个孤立点时，模板的响应最强，而在亮度不变的区域响应为0。

实现
若T已经给出

g = abs(imfilter(double(f),w))>=T;  
f：输入图像；
w：点检测模板；
T：指定的非负阈值；
g：包含检测点的输出图像

示例：图像中的孤立点检测

f = imread('test_pattern_with_single_pixel.tif');
w = [1 1 1; 1 -8 1; 1 1 1];
g = abs(imfilter(double(f),w));
T = max(g(:)); % 将滤波后的图像g的最大值设定为阈值T，很明显，g中不可能有比T值更大的点。
g = g >= T;

figure;
subplot(1,2,1); imshow(f); title('原图');
subplot(1,2,2); imshow(g); title('点检测图像');

由图可以看出，原图方框框的位置，有一个几乎看不见的小黑点，通过点检测的方法，在检测后的图像中，就能很明显的看到该点的存在。
点检测的另一种方法是在大小为m*n的所有邻域内寻找一些点，这些点的最大值和最小值之差超过了T。可以使用ordfilt2函数（排序）来实现。

g = imsubtract(ordfilt2(f,m*n,ones(m,n)),ordfilt2(f,1,ones(m,n)));
g = g >= T;

1.2 线检测

线检测会更复杂一些。对于线检测，二阶导数将产生更强的响应，并产生比一阶导数更细的线。
==注：==必须适当处理二阶导数的双线效应
线检测模板如下：

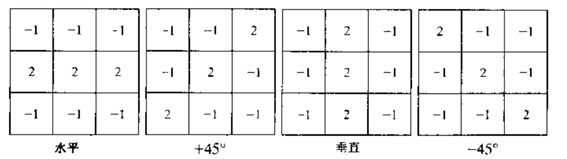
第一个模板对水平方向的线有最佳响应；第二个模板对45°方向的线有最佳响应；第三个模板对垂直方向的线有最佳响应；第四个模板对**-45°方向**的线有最佳响应。每个模板的首选方向用一个比其他方向更大的系数（如2）加权。每个模板中系数之和为0，表明恒定灰度区域中的响应为0。
注：有关正负45°模板中，不同的书有不同的说法，均与所选的坐标系及其方向有关，只要自己能搞清楚到底想要的是图像哪个方向的边缘即可，根据自己想要提取的对角的方向选择合适的模板即可，而不必纠结到底哪个模板是+45°，哪个是-45°。

若对检测图像中由给定模板定义的方向上的所有线感兴趣，则只须简单对图像运用这个模板，并对结果的绝对值进行阈值处理。留下的点是有最强响应的点，这些点与模板的方向最为接近，且组成了只有一个像素宽的线。

示例：寻找图像中所有宽度为1像素、方向为-45°的线。

f = imread('wirebond_mask.tif');
w = [2 -1 -1;-1 2 -1;-1 -1 2];
g = imfilter(double(f),w);

gtop = g(1:120,1:120); % 获取左上角的图像
gtop = pixeldup(gtop,4); % 将图像放大4*4倍

gbot = g(end -119:end,end -119:end);  % 获取右下角的图像
gbot = pixeldup(gbot,4);  % 将图像放大4*4倍

g1 = abs(g); 
T = max(g1(:));  % 将阈值设为g1的最大值
g2 = g1 >= T; % 对模板滤波的结果进行阈值处理

figure;
subplot(2,3,1),imshow(f),title('(a)原图');
subplot(2,3,2),imshow(g,[]),title('(b)45°方向处理后的图像');
subplot(2,3,3),imshow(gtop,[]),title('(c)左上角放大的图像');
subplot(2,3,4),imshow(gbot,[]),title('(d)右下角放大的图像');
subplot(2,3,5),imshow(g1,[]),title('(e)滤波后绝对值的图像');
subplot(2,3,6),imshow(g2),title('(f)阈值处理后的图像');

由于一个figure中显示的图太多，故有些图中的细节可能显示不完整，若想要观察每个图的具体细节，单独显示要观察的图就好。
从图b中可以看到，图中有明显的黑线和白线，这就是二阶导数的双线效应，中等灰度表示0，较暗的灰色调表示负值，较量的色调表示正值。放大图像会看的更明显。对图b求绝对值，可以消除图中的负值，如图e所示。
从图c和图d中的直线段相比，图d中的更亮，这是因为图a中右下角的线段宽度为1，而左上方线段的宽度不是。

1.3 边缘检测

边缘检测是基于灰度突变来分割图像的方法

1.3.1 边缘模型

边缘模型根据它们的灰度剖面分为：台阶模型、斜坡模型和屋顶模型。

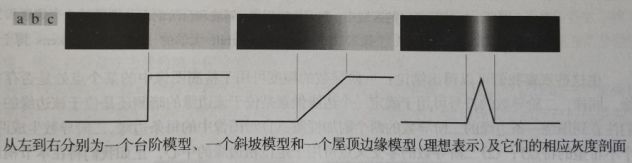
台阶边缘：理想型，1像素的距离上出现两个灰度级间的理想过渡。
斜坡边缘：实际中，数字图像都存在被模糊且带有噪声的边缘，因此更接近斜坡边缘，斜坡的斜度与边缘的模糊程度成正比。一个边缘点是斜坡中包含的任何点，一条边缘线段是一组已连接起来的这样的点。
屋顶边缘：屋顶模型是通过一个区域的线的模型，屋顶边缘的基底（宽度）由该线的宽度和尖锐度决定。

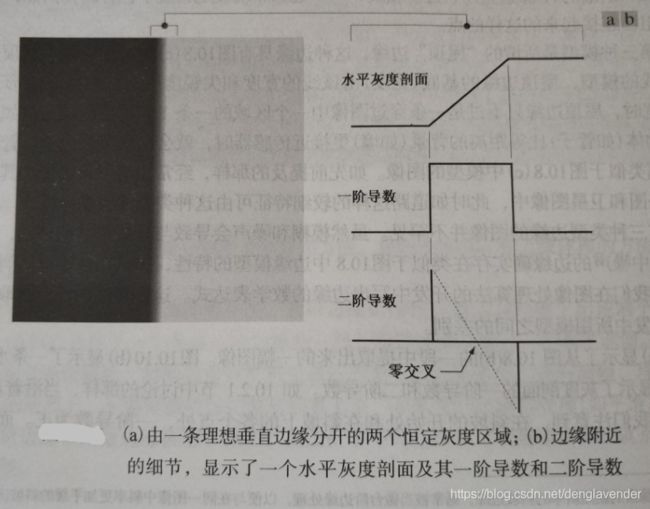
结论：
(1) 一阶导数的幅度可用于检测图像中的某个点处是否存在一个边缘；
(2) 二阶导数的符号可用于确定一个边缘像素是位于该边缘的暗侧还是位于该边缘的亮侧，为“正”在暗侧，为“负”在亮侧；
围绕一条边缘的二阶导数的两个附加性质：
a、对图像中的每条边缘，二阶导数生成两个值（一个不希望的特点）；
b、二阶导数的零交叉点（零灰度轴和二阶导数极值间的连线的交点）可用于定位粗边缘的中心

边缘检测的基本步骤：

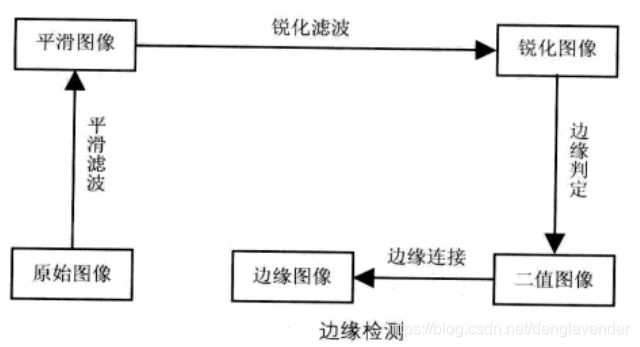
(1) 平滑滤波：由于梯度计算易受噪声影响，因此第一步是用滤波去噪。但是，降低噪声的平滑能力越强，边界强度的损失越大；
(2) 锐化滤波：为了检测边界，必须确定某点邻域中灰度的变换。锐化操作加强了存在有意义的灰度局部变化位置的像素点；
(3) 边缘判定：在图像中存在许多梯度不为零的点，但对于特定应用，不是所有点都有意义。这就要求我们根据具体情况选择和去除处理点，具体方法包括二值化处理和过零检测等；
(4) 边缘连接：将间断的边缘连接成有意义的完整边缘，同时去除假边缘。主要方法是Hough变换

1.3.2 基本边缘检测

图像梯度
图像f的(x,y)处边缘的强度和方向用梯度表征，梯度用∇f表示，用向量来定义：

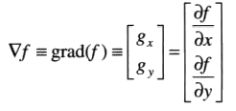
该向量指出了f在位置(x,y)处的最大变化率的方向。
∇f的大小（长度/赋值）表示为M(x,y)。

平方和平方根需要大量的计算开销，故常用的是用绝对值来近似梯度的大小（幅值）。

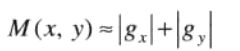
它是梯度向量方向变化率的值，M(x,y)常称为梯度图像。注：g_x，g_y和M(x,y)都是与原图像大小相同的图像。
梯度向量的方向由对于x轴度量的角度给出：

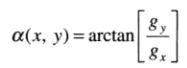
任意点(x,y)处一个边缘的方向与该点处梯度向量的方向α(x,y)正交。

梯度算子（一阶导数）
常见的梯度算子的模板如下：

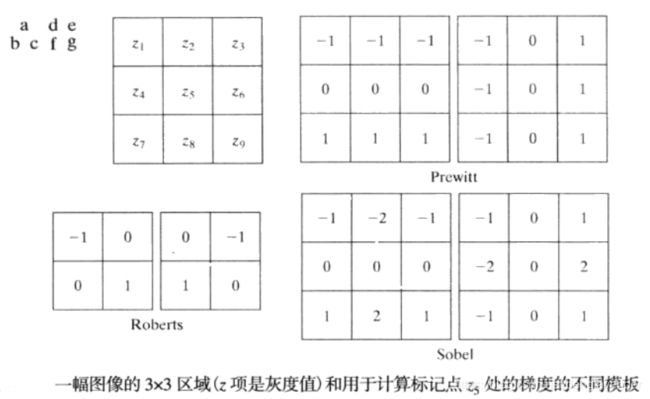
Roberts交叉梯度算子
具有对角优势的二维模板之一。

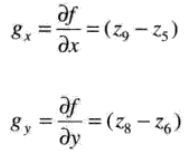
Prewitt算子
检测水平和竖直方向。

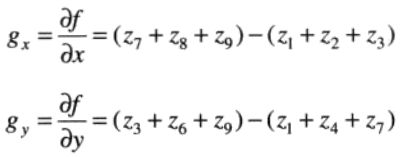
Sobel算子
与Prewitt模板类似，检测水平和竖直方向，但中心系数上使用一个权值2：

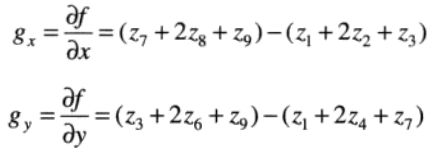
中心位置处使用2可以平滑图像。

用于检测对角线方向边缘的Prewitt和Sobel算子

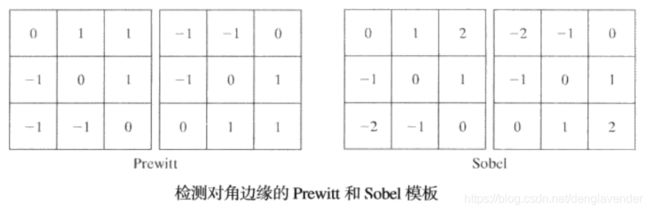
小结：
1、Roberts算子边缘定位精确度高，但易丢失一部分边缘，由于图像没经过平滑处理，故不具备抑制噪声的能力。该算子对具有陡峭边缘且含噪声少的图像效果较好。
2、Sobel算子和Prewitt算子都考虑了邻域信息，相当于对图像先做加权平滑处理，不同的是平滑部分的权值有差异，故对噪声具有一定的抑制能力，检测出的边缘容易出现多像素宽度。Prewitt模板比Sobel模板实现更简单，但Sobel模板抑制噪声能力更强。
3、当边缘检测的目的是突出主要边缘并尽可能保持连接时，实践中通常对图像先进行平滑处理，在边缘检测完之后，对边缘结果再进行阈值处理。

1.3.3 更先进的边缘检测技术

这些技术是通过考虑如图像噪声和边缘本身特性等因素来改善简单的边缘检测方法。
高斯拉普拉斯算子（LoG）
拉普拉斯算子是一个二阶导数，对噪声具有无法接受的敏感性，而且其幅值会产生双线效应，另外，边缘方向的不可检测也是其的缺点之一，故一般不以其原始形式作用域边缘检测。
G(x,y)为高斯函数为：

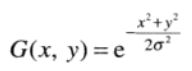
其中σ是标准差。用高斯函数卷积模糊一幅图像，图像的模糊程度是由σ决定的。
高斯拉普拉斯算子为∇²G(x,y)：

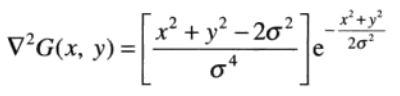
常见的LoG模板

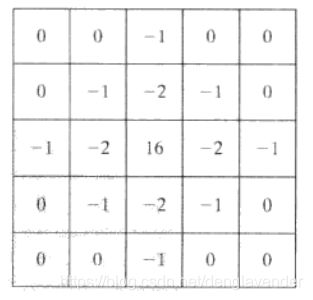
实际中使用的是该模板的负值。
算法步骤：
1、对输入图像使用n*n高斯低通滤波器进行滤波；
2、计算滤波后图像的拉普拉斯；

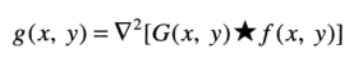
3、寻找g(x,y)的零交叉来确定f(x,y)中边缘的位置。
高斯低通滤波器大小的选择，即n值应是大于等于6σ的最小奇整数。

坎尼边缘检测器（Canny算子）
前面介绍的几种基于微分方法的边缘检测算法，都是只有在图像不含噪声或者先通过平滑去噪的前提下才能正常使用。
在图像边缘检测中，抑制噪声和边缘精确定位是无法同时满足的。Canny算子力图在抗噪声干扰和精确定位之间寻求最佳这种方案。
Canny方法基于三个基本目标：
1、低错误率。所有边缘都应该被找到，并且应该没有伪响应。即检测到的边缘必须尽可能是真实的边缘。数学上，就是使信噪比SNR尽量大，输出信噪比越大，错误率越少。
2、边缘点应被很好地定位。已定位边缘必须尽可能接近真实边缘。即由检测器标记为边缘的点和真实边缘的中次年之间的距离应该最小。
3、单一的边缘点响应。对于真实的边缘点，检测器仅应返回一个点。即真实边缘周围的局部最大数应该是最小的。这意味着在仅存一个单一边缘点的位置，检测器不应指出多个边缘像素。

算法步骤：
1、用一个高斯滤波器（n*n大小）平滑输入图像；
2、用一阶偏导的有限差分来计算梯度幅值图像和角度图像；
3、对梯度幅值图像应用非最大抑制；
4、用双阈值处理和连接分析来检测并连接边缘

1.3.4 边缘检测方法的matlab实现

使用edge函数可以方便地实现上述几种边缘检测方法。该函数的作用是检测灰度图像中的边缘，并返回一个带有边缘信息的二值图像，其中黑色表示背景，白色表示原图像的边缘部分。
参考：edge函数
默认情况下，edge函数使用Sobel算子进行边缘检测。
基于梯度算子的边缘检测

BW = edge(I,type,thresh,direction,'nothinning')
[BW,threshOut] = edge(I,type,thresh,direction,'nothinning')

I：需要检测边缘的输入图像，为灰度图像或二值图像。
type：表示梯度算子的种类。

thresh：敏感度阈值参数，任何灰度值低于此阈值的边缘将不会被检测到。其默认值是空矩阵[]，此时算法会自动计算阈值。
direction：指定了我们感兴趣的边缘方向，edge函数将只检测到direction中指定方向的边缘，默认的是both。
注：如果选择 Roberts 算子，则 ‘horizontal’ 方向实际上检测到与水平方向成 135° 角的边缘，‘vertical’ 方向检测到与水平方向成 45° 角的边缘。

可选参数’nothinning’，指定时可以通过跳过边缘细化算法来加快算法运行的速度。默认时候，这个参数是’thinning’，即进行边缘细化。
BW：返回的二值图像，其中0（黑色）为背景，1（白色）为边缘部分。
threshOut：返回阈值。若指定阈值了，则threshOut = thresh，若不指定阈值，则返回自动确定的阈值。

基于高斯-拉普拉斯算子的边缘检测

BW = edge(I,'log',thresh,sigma)

‘log’：表示高斯-拉普拉斯算子。
thresh：敏感度阈值参数。如果将thresh设为0，则输出的边缘图像将包含围绕所有物体的闭合的轮廓线，因为这样的运算会包括输入图像中所有的过零点。
sigma：指定生成高斯滤波器所使用的标准差。默认为2。滤镜大小n x n，n的计算方法为n = ceil(sigma*3)*2 + 1。
BW为返回的二值图像，其中0（黑色）为背景，1（白色）为边缘部分。
零交叉检测器：

BW = edge(I,'zerocross',thresh,h) % 使用指定的滤波器 h 检测边缘。

基于Canny算子的边缘检测

BW = edge(I,'canny',thresh,sigma)

Canny算子是edge函数中最强的边缘检测算子
‘Canny’：表示canny算子
thresh：敏感度阈值参数，其默认值是空矩阵[]。Canny算法的敏感度阈值是一个列向量，因为需要为算法指定阈值的上下限。忽略边缘强度低于下阈值的所有边缘，保留边缘强度高于上阈值的所有边缘。在指定阈值矩阵时，第1个元素是阈值下限，第2个元素为阈值上限。如果只指定一个阈值元素，则这个直接指定的值会被作为阈值上限，而它与0.4的乘积会被作为阈值下限。如果阈值参数没有指定，算法会自行确定敏感度阈值的上下限。
sigma：指定生成平滑使用的高斯滤波器的标准差。默认为1。滤镜大小n x n，n的计算方法为n = ceil(sigma*3)*2 + 1。

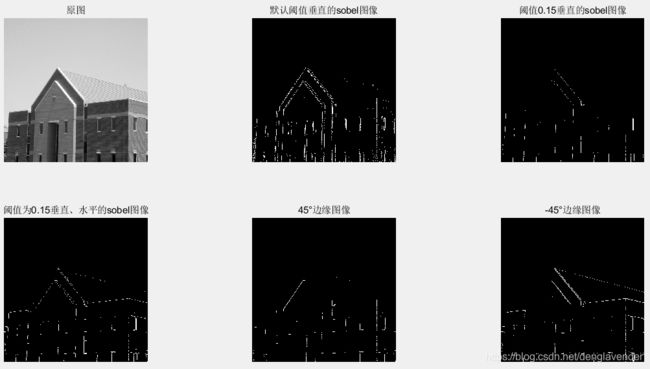
示例：使用Sobel算子来提取边缘

f = imread('building.tif');
[gv,t] = edge(f,'sobel','vertical'); % 提取垂直边缘
% 主要边缘是垂直边缘（倾斜的边缘也有垂直分量和水平分量），故倾斜边缘也能被检测到
t  % 默认阈值为0.0516
gv1 = edge(f,'sobel',0.15,'vertical');  %  自行指定一个较高的阈值，将弱一些的边缘去掉，如0.15

gboth = edge(f,'sobel',0.15); % 水平和垂直边缘

wneg45 = [-2 -1 0;-1 0 1;0 1 2];  % 用于提取45°方向的边缘
w45 = [0 1 2;-1 0 1;-2 -1 0];  % 用于提取-45°方向的边缘
gneg45 = imfilter(double(f),wneg45,'replicate');
g45 = imfilter(double(f),w45,'replicate');
T =0.3*max(abs(gneg45(:)));
gneg45 = gneg45>=T;
g45 = g45 >= T;

figure;
subplot(2,3,1); imshow(f); title('原图');
subplot(2,3,2); imshow(gv);title('默认阈值垂直的sobel图像');
subplot(2,3,3); imshow(gv1); title('阈值0.15垂直的sobel图像');
subplot(2,3,4); imshow(gboth); title('阈值为0.15垂直、水平的sobel图像');
subplot(2,3,5); imshow(gneg45);title('45°边缘图像');
subplot(2,3,6);imshow(g45); title('-45°边缘图像');

示例：五种边缘检测算法的比较

f = imread('building.tif');
bw1 = edge(f,'sobel');
bw2 = edge(f,'prewitt');
bw3 = edge(f,'roberts');
bw4 = edge(f,'log');
bw5 = edge(f,'canny');

figure;
subplot(2,3,1); imshow(f); title('原图');
subplot(2,3,2); imshow(bw1); title('sobel检测');
subplot(2,3,3); imshow(bw2); title('prewitt检测');
subplot(2,3,4); imshow(bw3); title('roberts检测');
subplot(2,3,5); imshow(bw4); title('log检测');
subplot(2,3,6); imshow(bw5); title('canny检测');

分析：
1、从边缘定位的精度看：
Roberts算子和Log算子定位精度较高。
Roberts算子简单直观，Log算子利用二阶导数零交叉特性检测边缘。但Log算子只能获得边缘位置信息，不能得到边缘的方向等信息。
2、从对不同方向边缘的响应看
从对边缘方向的敏感性而言，Sobel算子、Prewitt算子检测斜向阶跃（灰度突变）边缘效果较好，Robets算子检测水平和垂直边缘效果较好。Log算子不具备边缘方向检测能力。
Sobel算子可以提供最精确的边缘方向估计。
3、从去噪能力看
Roberts和Log算子定位精度虽然较高，但受噪声影响大。
Sobel算子和Prewitt算子模板相对较大因为去噪能力较强，具有平滑作用，能滤除一些噪声，去掉部分伪边缘，但同时也平滑了真正的边缘，这也正是其定位精度不高的原因。

从总体效果来衡量，Canny算子给出了一种边缘定位精确性和抗噪声干扰性的较好折中。

当有成本和速度限制时，通常使用阈值梯度边缘检测方法。当追求边缘质量时，通常会选择Log和Canny算子，Canny算子效果更好。

1.3.5 Hough变换

理想情况下，边缘检测应该仅产生位于边缘上的像素集合。实际上，由于噪声、不均匀照明引起的边缘间断，以及其他引入灰度值虚假的不连续的影响，这些像素并不能完全描述边缘特性。因此，一般是在边缘检测后紧跟连接算法，将边缘像素组合成有意义的边缘或区域边界。
Hough变换是一个非常重要的检测间断点边界形状的方法。通过将图像坐标空间变换到参数空间，来实现直线和曲线的拟合。

原理：
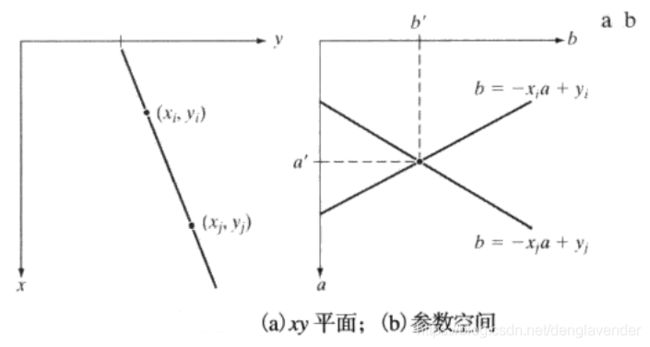
直角坐标参数空间
在x-y坐标空间中，经过点(x_i,y_i)的直线表示为y_i = ax_i + b，a为斜率，b为截距。
通过点(x_i,y_i)的直线有无数条，对应的a和b也不尽相同。
若将x_i和y_i看作常数，将a和b看作变量，从x-y空间变换到a-b参数空间。则点(x_i,y_i)处的直线变为b = -x_ia + y_i。x-y空间的另一点(x_j,y_j)处的直线变为b = -x_ja + y_j。
x-y空间中的点在a-b空间中对应一条直线，若点(x_i,y_i)和(x_i,y_i)在x-y空间共线，则在a-b空间对应的两直线相交于一点(a’,b’)。反之，在a-b空间相交于同一点的所有直线，在x-y空间都有共线的点与之对应。

具体计算：
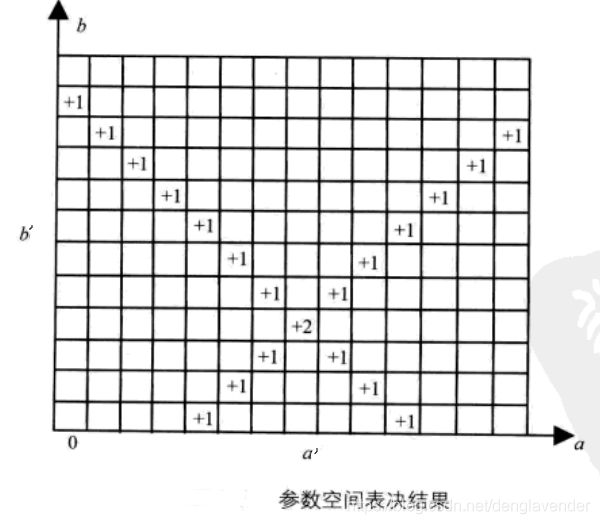
将a-b空间视为离散的。建立二维累加数组A(a,b)，第一维是x-y空间中直线斜率的范围，第二维是直线截距范围。二维累加数组A也常被称为Hough矩阵。
初始化A(a,b)为0。
对x-y空间的每个前景点(x_i,y_i)，将a-b空间的每个a带入b = -x_ia + y_i，计算对应的b。
每计算出一对(a,b)，对应的A(a,b) = A(a,b) + 1。
所有计算结束后，在a-b空间找最大的A(a,b)，即峰值。峰值所对应的(a’,b’)参考点就是原图像中共线点数目最多的直线方程的参数。

求出参考点后，整个目标的边界就可以确定了。

极坐标参考空间
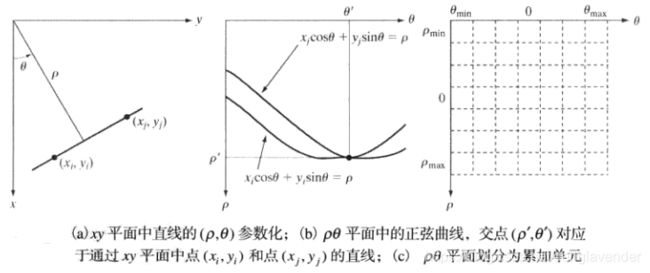
使用直角坐标表示直线时，当直线为一条垂直直线或接近垂直直线时，该直线的斜率为无限大或接近无限大，故在a-b空间中无法表示，因此要在极坐标参考空间解决这一问题。
直线的法线表示为：xcosθ + ysinθ = ρ
ρ：直线到原点的垂直距离，取值范围为[-D,D]，D为一幅图像中对角间的最大距离；θ：x轴到直线垂直线的角度，取值范围为[-90°,90°]。
极坐标中的Hough变换，是将图像x-y空间坐标变换到ρ-θ参数空间中。x-y空间中共线的点变换到ρ-θ空间后，都相交于一点。不同于直角坐标的是，x-y空间共线的点(x_i,y_i)和(x_j,y_j)映射到ρ-θ空间是两条正弦曲线，相交于点(ρ‘,θ’)。
具体计算时，也要在ρ-θ空间建立一个二维数组累加器A。除了ρ和θ的取值范围不同，其余与直角坐标类似，最后得到的最大的A所对应的(ρ,θ)。

Hough也能处理其他任意形状的函数。

matlab实现
通过Hough变换在二值图像中检测直线的3个步骤：

• 用hough函数执行霍夫变换，得到霍夫矩阵；
• 用houghpeaks函数在霍夫矩阵中寻找峰值点；
• 用houghlines函数在原二值图像上提取线段

1、霍夫变换——hough
hough函数对一幅二值图像执行Hough变换，得到Hough矩阵。调用格式为：

 [H,theta,rho] = hough(f)   
 或 [H,theta,rho] = hough(f,'ThetaRes',val1,'RhoRes',val2) 

其中，H是霍夫变换矩阵，theta和rho是ρ和θ值向量。f是二值图像，val1是0-90的标量，指定沿θ轴单位区间的间距（默认为1）；val2可取(0,norm(size(f))区间上的实数，指定沿ρ轴单位区间的间距（默认为1）。
2、寻找峰值——houghpeaks
在Hough矩阵中寻找指定数目的峰值点。调用格式为：

peaks = houghpeaks(H,NumPeaks)
或 peaks = houghpeaks(H,NumPeaks，‘Threshold’,val1,'NHoodSize',val2)

H：从hough函数得到的霍夫矩阵
Numpeaks：要寻找的峰值数目，默认为1
Threshold：峰值的阈值，只有大于该阈值的点才被认为是可能的峰值，val1可以从0到Inf变换，默认是0.5 x max(H(：))
NHoodSize：在每次检测出一个峰值后，NHoodSize指出在该峰值周围需要清零的邻域信息。以向量[M,N]的形式给出，其中M、N均为正的奇数，默认为≥size(H)/50的最小奇数。
peaks：是一个Q*2的矩阵，每行的两个元素分别为某一峰值点在Hough矩阵中的行、列索引，Q为找到的峰值点的数目。
3、提取直线段——houghlines
根据Hough矩阵的峰值检测结果提取直线段。调用格式为：

lines = houghlines(f,theta,rho,peaks)
或lines = houghlines(f,theta,rho,peaks,'FillGap',val1,'MinLength',val2)

theta 和 rho 是函数 hough 返回的向量。peaks 是由 houghpeaks 函数返回的矩阵。
FillGap：线段合并的阈值，如果对应于Hough矩阵某一单元格（相同的ρ和θ）的2个线段之间的距离小于FillGap，则合并为1个直线段，默认值为20。
MinLength：检测直线段的最小长度阈值，如果检测出的直线段长度大于MinLength，则保留，丢弃所有长度小于MinLength，默认值为40。
lines：是一个结构体数组，数组长度是找到的直线条数，而每一个数组元素的内部结构如下：

域	含义
point1	直线段的端点1坐标
point2	直线段的端点2坐标
theta	对应在霍夫矩阵中的θ
rho	对应在霍夫矩阵中的ρ

示例：使用霍夫变换连接边缘

I  = imread('building.tif'); 

% 获取图像边缘（二值图像）
BW = edge(I,'canny');    

% 执行Hough变换并显示Hough矩阵
[H,T,R] = hough(BW);
imshow(H,[],'XData',T,'YData',R,'InitialMagnification','fit');
xlabel('\theta'), ylabel('\rho');
axis on, axis normal, hold on;

% 在Hough矩阵中寻找前5个大于Hough矩阵中最大值0.3倍的峰值
P  = houghpeaks(H,5,'threshold',ceil(0.3*max(H(:))));
x = T(P(:,2)); y = R(P(:,1));  % 由行、列索引转换成实际坐标
plot(x,y,'s','color','white');  % 在Hough矩阵图像中标出峰值位置

% 找到并绘制直线
lines = houghlines(BW,T,R,P,'FillGap',20,'MinLength',10);  % 合并距离小于20的线段，丢弃所有长度小于10的直线段
figure, imshow(I), hold on
max_len = 0;
for k = 1:length(lines)  % 依次标出各条直线段
   xy = [lines(k).point1; lines(k).point2];  % xy中包含一条线段的起点和终点坐标
   plot(xy(:,1),xy(:,2),'LineWidth',2,'Color','green');  % 线为绿色

   % 绘制线段端点
   plot(xy(1,1),xy(1,2),'x','LineWidth',2,'Color','yellow');  % 起点为黄色
   plot(xy(2,1),xy(2,2),'x','LineWidth',2,'Color','red');  % 终点为红色

   % 确定最长的线段
   len = norm(lines(k).point1 - lines(k).point2);
   if ( len > max_len)
      max_len = len;
      xy_long = xy;
   end
end

% 高亮显示最长的线段
plot(xy_long(:,1),xy_long(:,2),'LineWidth',2,'Color','cyan'); 

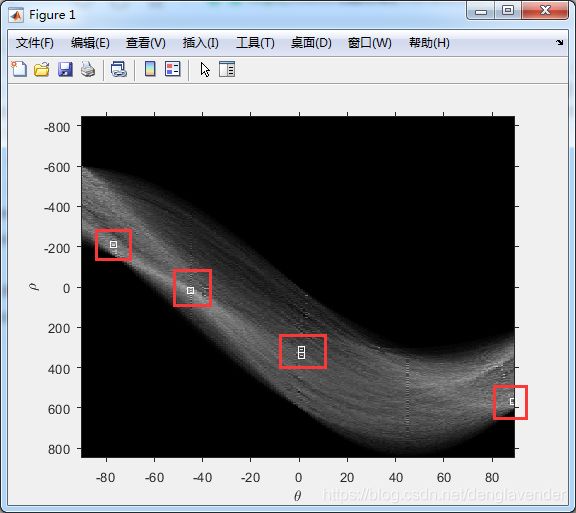
方框框出来的为峰值在参数空间中的位置

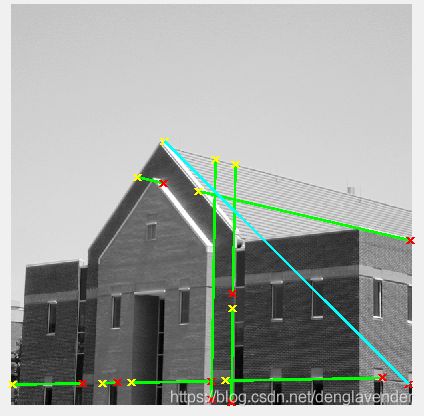
将提取出来的直线段叠加在原图中，并对直线加以标注。

注：Hough只能处理二值图像，一般在执行变换前需要在图像上执行边缘检测。

三、阈值处理

图像阈值处理在图像分割应用中处于核心地位。

3.1 基础知识

一般情况下，一幅图像由前景部分和背景部分构成，我们感兴趣的一般的是前景部分，所以一般用阈值将前景和背景分割开来，使我们感兴趣的图像像素值为1，不感兴趣的为0；有时一张图我们会有几个不同的感兴趣区域（不在同一个灰度区域），这时我们可以用多个阈值进行分割。
单阈值处理

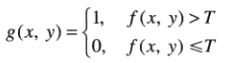
T为阈值。此时T适用于整个图像，该处理称为全局阈值处理。
双阈值处理

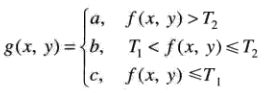
T₁和T₂分别为不同的阈值，a、b和c是三个不同的灰度值。

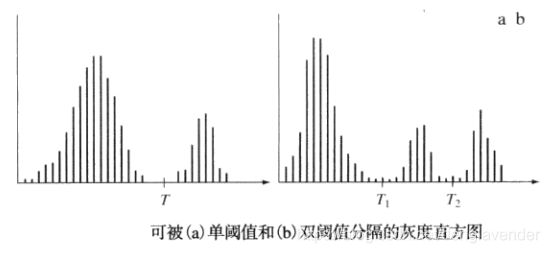
灰度阈值的成功与否直接关系到可区分直方图模式（即不同的感兴趣区域，可能不止一个）的波谷的宽度和深度，波谷越宽且越深，则越易进行阈值处理。
影响波谷特性的关键因素：1）波峰间的间隔（波峰离得越远，分离这些模式的机会越大）；2）图像中的噪声内容（模式的波峰随噪声的增加而展宽）；3）物体和背景的相对尺寸；4）光源的均匀性；5）图像反射特性的均匀性。

3.2 基本的全局阈值处理

当物体和背景像素的灰度分布十分明显时，可用适用于整个图像的单个阈值。下面介绍为每幅图像自动估计阈值的算法。算法描述如下：
1）为全局阈值T选择一个初始估计值（建议初始估计值设为图像最大灰度值和最小灰度值的中间值）；
2）使用阈值T分割该图像。将产生两组像素：G₁由灰度值大于T的所有像素组成，G₂由灰度值小于T的所有像素组成。
3）对G₁和G₂的像素分别计算平均灰度值m1和m2；
4）计算新阈值：T = 1/2(m1 + m2)；
5）重复步骤2~4，直到在连续的重复中，T的差异比预先设定的参数小为止。

使用imbinarize进行阈值分割图像

BW = imbinarize(I,T)

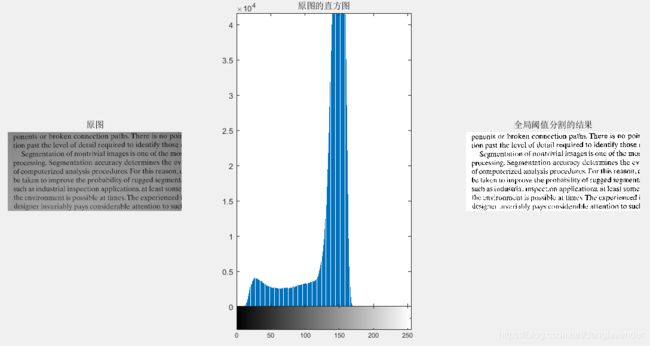
f = imread('scanned-text-grayscale.tif');
count = 0;
T = mean2(f); % 初始化阈值T，求整个矩阵像素的平均值
done = false;
while ~done
count  = count+1;  % 记录迭代次数
g = f>T;
Tnext = 0.5*(mean(f(g))+mean(f(~g)));
done = abs(T-Tnext)<0.5;
T = Tnext;
end

g = imbinarize(f,T/255);  % 需要将阈值归一化
subplot(1,3,1); imshow(f); title('原图');
subplot(1,3,2); imhist(f); title('原图的直方图');
subplot(1,3,3); imshow(g); title('全局阈值分割的结果');

3.3 用Otsu方法的最佳全局阈值处理

Otsu是一种基于图像直方图的方法。
图像的阈值处理也可以理解为把像素分配个两个或多个类。Otsu采用最大化类间方差的方法，来确定图像分割的最佳阈值k。

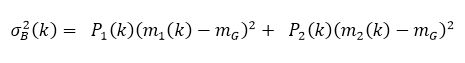
σ_B² (k)为类间方差；P₁(k)为阈值k时，像素被分到类C₁中的概率；m₁(k)为分配到类C₁的像素的平均灰度值；m_G为整个图像的平均灰度值；P₁(k)和m₁(k)与1类似。
当设置的方差越大，则越接近正确分割一幅图像的阈值。上式中的k就是我们所要寻找的最佳阈值，当k不唯一时，则将所有的最佳阈值进行取平均值即可。

实现
graythresh 使用 Otsu 方法计算全局图像阈值。调用格式如下

T = graythresh(I)
[T,EM] = graythresh(I)  
% I为灰度图像；T为归一化阈值；
% EM为阈值的有效性度量，以范围 [0,1] 内的正标量形式返回。下界只能由具有单一灰度级的图像获得，上界只能由二值图像获得。一般来说，高EM值说明灰度分成两类的可能性比较高。

示例

f = imread('scanned-text-grayscale.tif');
T = mean2(f); % 初始化阈值T，求整个矩阵像素的平均值
done = false;
while ~done
g = f>T;
Tnext = 0.5*(mean(f(g))+mean(f(~g)));
done = abs(T-Tnext)<0.5;
T =Tnext;
end
T
g = imbinarize(f,T/255);  % 需要将阈值归一化

[T1,EM] = graythresh(f);
EM
T1*255
g1 = imbinarize(f,T1);
subplot(2,2,[1,2]); imshow(f); title('原图');
subplot(2,2,3); imshow(g); title('基本全局阈值分割的结果');
subplot(2,2,4); imshow(g1); title('Ostu最佳阈值处理');

从这个小例子中，我们看不出来基本全局阈值处理和Ostu最佳阈值处理的区别，但对于某些图像的直方图没有明显的波谷的情况，Ostu方法的阈值处理效果会更好。

3.4 用图像平滑改善全局阈值处理

噪声会对图像的阈值处理产生很大的影响。当噪声不能在源头减少时，在阈值处理之前可以先对图像进行平滑处理，以便后续进行更好的阈值处理。

f = imread('cygnusloop_Xray_original.tif');
f = uint8(f);
T = graythresh(f);
g = imbinarize(f,T);

w = fspecial('average',5);
fa = imfilter(f,w,'replicate');

Ta = graythresh(fa);
ga =imbinarize(fa,Ta);
figure;
subplot(2,3,1); imshow(f); title('带有噪声的图像');
subplot(2,3,2); imhist(f); title('噪声图像直方图');
subplot(2,3,3); imshow(g); title('Ostu对噪声图像的处理结果');
subplot(2,3,4); imshow(fa); title('去噪图像');
subplot(2,3,5); imhist(fa); title('去噪图像直方图');
subplot(2,3,6); imshow(ga); title('Ostu对去噪图像的处理结果');

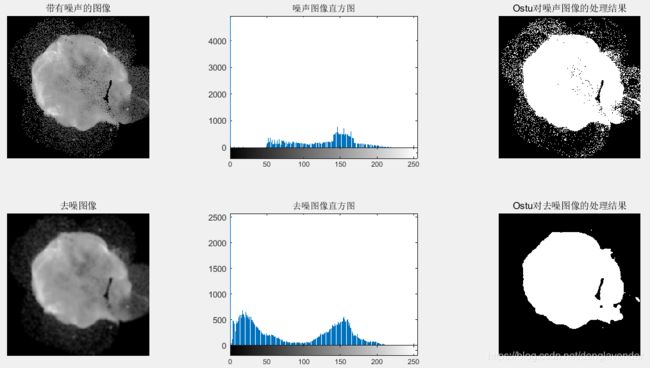
由原图的直方图可以看出，几乎观察不到要进行分类的不同类别的波谷，因此分割出来的结果就不是很好，对图像使用均值滤波器先进行平滑处理（去噪）后再进行阈值处理，分割的效果就很好了。

3.5 利用边缘改进全局阈值处理

对于边界明显的图像，前景和背景面积悬殊，但是整体灰度值相近，不易用otsu直接找出正确的阈值，可以使用边缘改进的阈值处理。
边缘改进的阈值处理：主要是处理那些位于或接近物体和背景间边缘的像素，使得这些像素分离开的操作。
算法描述：
1）计算一副边缘图像（梯度和拉普拉斯都可以）。
2）指定一个阈值T。通常通过百分比指定阈值，常选择边缘图像直方图中百分比相对高（如90%）的值作为阈值（边缘图像直方图中的较高的值表示边缘比较强烈的部分）。
3）用步骤2中的阈值对步骤1中产生的图像进行阈值处理，产生一副二值图像g_T(x,y)。将选择出来的“强”边缘像素的二值图像作为模板。
4）使用g_T(x,y)与原图像f(x,y)相乘，得到一幅新图像，相当于使原图像中的物体和背景对比的更明显。
5）对新图像进行阈值分割，如Ostu方法。
代码是参考网上的，本人没有弄的很清楚
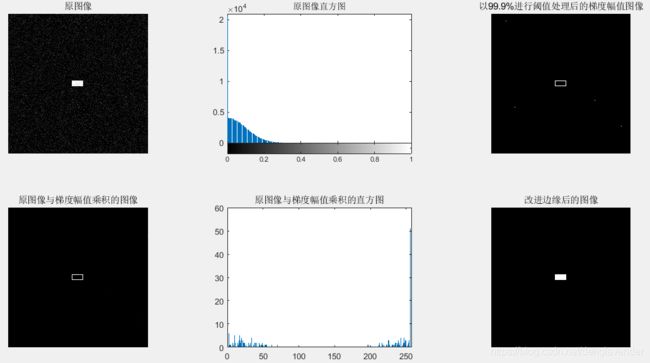
示例1：基于梯度边缘信息改进全局阈值处理

f = double(imread('noisy-image.tif'));
f = imnoise(f,'gaussian');
subplot(231),imshow(f),title('原图像');
subplot(232),imhist(f),title('原图像直方图');
% 计算梯度
sx = fspecial('sobel');
sy = sx';
gx = imfilter(f,sx,'replicate');
gy = imfilter(f,sy,'replicate');
grad = sqrt(gx.*gx+gy.*gy);
grad = grad/max(grad(:));

% 得到grad的直方图，并使用高的百分比（99.9%）估计梯度的阈值
h =imhist(grad);
Q = percentile2i(h,0.999);
% 用Q对梯度做阈值处理，形成标记图像，并且从f中提取梯度值比Q大的点，得到结果的直方图
markerImage = grad>Q;
subplot(233),imshow(markerImage),title('以99.9%进行阈值处理后的梯度幅值图像');
fp = f.*markerImage;
subplot(234),imshow(fp),title('原图像与梯度幅值乘积的图像');
hp = imhist(fp);
% 用结果的直方图得到Otsu阈值
hp(1) = 0;
subplot(235),bar(hp),title('原图像与梯度幅值乘积的直方图');
T = otsuthresh(hp);
T*(numel(hp)-1)
g = imbinarize(f,T);
subplot(236),imshow(g),title('改进边缘后的图像')

示例2：用拉普拉斯边缘信息改进全局阈值处理

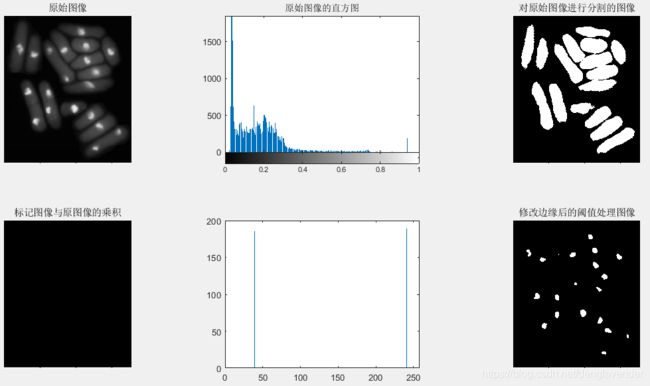
f = im2double(rgb2gray(imread('test_img.png')));
subplot(231),imshow(f,[]),title('原始图像');
subplot(232),imhist(f),title('原始图像的直方图');
hf = imhist(f);
Tf = graythresh(f);
gf = imbinarize(f,Tf);
subplot(233),imshow(gf,[]),title('对原始图像进行分割的图像');
w = [-1 -1 -1;-1 8 -1;-1 -1 -1];
lap = abs(imfilter(f,w,'replicate'));
lap = lap/max(lap(:));
h = imhist(lap);
Q = percentile2i(h,0.995);
markerImage = lap >Q;
fp = f.*markerImage;
subplot(234),imshow(fp,[]),title('标记图像与原图像的乘积');
hp = imhist(fp);
hp(1) =0;
subplot(235),bar(hp)
T = otsuthresh(hp);
g = imbinarize(f,T);
subplot(236),imshow(g,[]),title('修改边缘后的阈值处理图像')

3.6 基于局部统计的可变阈值处理

在背景光照不均匀的情况下，或者在有多个主要物体灰度的情况下，此时使用全局阈值处理则不太合适，为此引入局部可变阈值处理。
我们用一幅图像中每个点(x,y)的邻域中像素的标准差和均值，分别表示局部对比度和平均灰度这两个描述子。
令σ_xy和m_xy表示一幅图像中以坐标(x,y)为中心的邻域S_xy所包含的像素集合的标准差和均值。则可变局部阈值T_xy为：

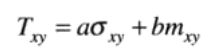
其中a和b为非负常数，a和b的值通常是通过实验确定的。且

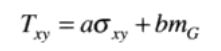
其中m_G为全局图像均值。

实现
计算局部标准差，使用函数stdfilt进行操作

g = stdfilt(f,nhood)
nhood 是由 0 和 1 组成的数组，其中非零元素指定用于计算局部标准差所用的领域。nhood 的尺寸在每个维度上必须是奇数，默认值是 ones(3)。

计算局部均值，可以用函数localmean进行操作
localmean.m

function mean = localmean(f,nhood)
if nargin ==1
    nhood = ones(3)/9;
else
    nhood = nhood/sum(nhood(:));
end
mean = imfilter(tofloat(f),nhood,'replicate');

局部阈值处理操作，用函数localthresh来操作
localthresh.m

function g = localthresh(f,nhood,a,b,meantype)
f = tofloat(f);
SIG = stdfilt(f,nhood);
if nargin == 5 && strcmp(meantype,'global')
    MEAN = mean2(f);
else
    MEAN = localmean(f,nhood);
end
g = (f > a*SIG) & (f > b*MEAN);

示例

f = im2double(rgb2gray(imread('test_img.png')));
subplot(2,2,1),imshow(f);title('(a) 原图');
[TGlobal] = graythresh(f); 
gGlobal = imbinarize(f, TGlobal); 
subplot(2,2,2),imshow(gGlobal);title('(b)用 Otsus 方法分割的图像');
g = localthresh(f, ones(3), 30, 1.5, 'global'); 
SIG = stdfilt(f, ones(3));
subplot(2,2,3), imshow(SIG, [ ]) ;title('(c) 局部标准差图像');
subplot(2,2,4),imshow(g);title('(d)  用局部阈值处理分割的图像 ');

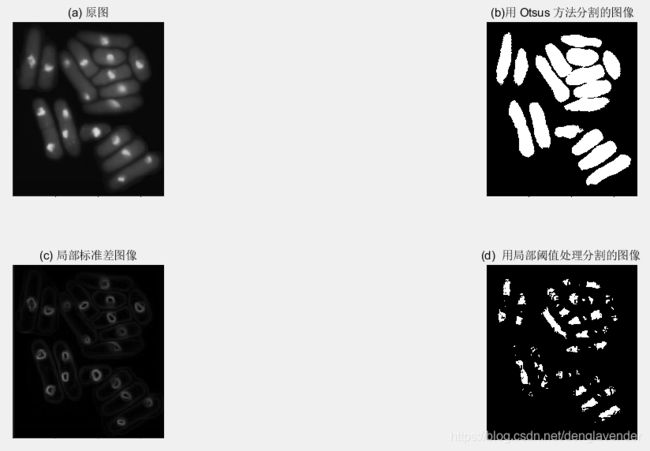
当背景接近于常数，并且所有物体的灰度高于或低于背景灰度时，选择全局均值一般会得到较好的结果。

3.7 使用移动平均的图像阈值处理

移动平均是一种局部阈值处理方法，该方法以一幅图像的扫描行计算移动平均值为基础。移动平均分割能减少光照偏差，且计算简单。当感兴趣的物体与图像尺寸相比较小(或较细)时，基于移动平均的阈值处理会工作的很好。适合于处理打印图像和手写文本图像。
为减少光照偏差，扫描是以Z字形模式逐行执行的。令z_k+1表示在扫描序列中第k+1步遇到的点的灰度。该新点处的移动平均（平均灰度）如下：

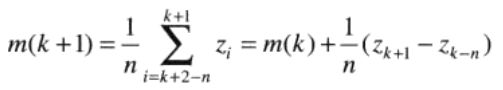
n表示用于计算平均的点的数量。
使用下式进行分割：

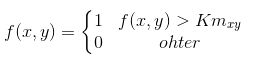
其中K是[0,1]区间的常数， m_xy是输入图像中点（x,y）处的移动平均（即上式的计算平均移动）。
使用movingthresh函数来实现移动平均操作：
movingthresh.m

function g = movingthresh(f, n, K)
f = im2double(f);
[M, N] = size(f);
if (n < 1) || (rem(n, 1) ~= 0)
error('n must be an integer >= 1.')
end
if K < 0 || K > 1
error('K must be a fraction in the range [0, 1].')
end
f(2:2:end, :) = fliplr(f(2:2:end, :));
f = f'; 	% Still a matrix.
f = f(:)'; % Convert to row vector for use in function filter.
maf = ones(1, n)/n; 	% The 1-D moving average filter.
ma = filter(maf, 1, f); % Computation of moving average.
g = f > K * ma;
g = reshape(g, N, M)';
g(2:2:end, :) = fliplr(g(2:2:end, :));

示例：用移动平均的文档阈值处理

f = imread('noisy-text.png');
f = rgb2gray(f);
% 使用Ostu全局阈值分割
T =graythresh(f);
g1 = imbinarize(f,T);
% 移动平均局部阈值分割
g2 = movingthresh(f,20,0.5);
figure;
subplot(1,3,1); imshow(f); title('原始图像');
subplot(1,3,2); imshow(g1); title('用otsu全局阈值分割后的图像');
subplot(1,3,3); imshow(g2); title('用移动平均局部阈值分割后的图像');

关于n的选取，经验之一是令n等于平均笔画宽度的5倍，在此图像中，平均宽度为4像素，故n取20。
原图是一幅以斑点灰度模式遮蔽的手写文本图像，用Ostu方法处理不能克服灰度的变化。很明显使用移动平均局部阈值处理分割能得到更好的效果。

四、基于区域的分割

以直接寻找区域为基础的分割技术。

4.1 区域生长

区域生长：根据预先定义的生长准则，将像素或子区域组合为更大区域的过程。
基本思想：从一组“种子”点（种子点可以是单个像素，也可以为某个小区域）开始，将与种子性质相似的邻域像素或区域与种子点合并，形成新的种子点，重复此过程直到不能生长为止。种子点和邻域区域的相似性判据可以是灰度值、纹理、颜色等多种图像信息。
算法步骤：
1、选择合适的种子点；
2、确定相似性准则即生长准则；
3、确定生长停止条件。
一般来说，在无像素或者区域满足加入生长区域的条件时，区域生长就会停止。

用一个简单的例子来说明区域生长的过程：图(a)为原图像，数字表示像素的灰度值，以灰度为8的像素为初始的种子点。在8邻域内，生长准则是待测点灰度值和种子点灰度值相差为1或0。当合并到图d后，其他像素点已经不满足生长生长准则，故停止生长。

实际中，区域生长时经常还要考虑到生长的“历史”，还要根据区域的尺寸、形状等图像的全局性质来决定区域的合并。

实现：
通过自定义regiongrow函数来实现区域增长：

[g,NR,SI,TI] = regiongrow(f,S,T)

f：将要被分割的图像
S： 可以是一个数组（与 f 大小相同）或一个标量。若 S 是一个数组，则它在所有种子点的坐标处必须是 1，而在其他位置为 0。若S 是一个标量，则它定义一个灰度值， f 中具有该值的所有点都会成为种子点。
T： 可以是一个数（与f大小相同）组或一个标量。若 T 是数组，则它对 f 中的每个位置包含一个阈值。若 T 是标量，则它定义一个全局阈值。阈值用来测试图像中的像素是否与该种子或8连接种子足够相似。
例如：若S = a，且T = b，则我们将比较亮度，若 |像素亮度 - a| ≤ b，则称该像素类似于a。另外，若问题中的像素是8连接到一个或多个种子值的，则这个像素可看作是一个或多个区域的成员。
g： 是分割后的图像，每个区域的成员都用整数标出。
NR： 是所找到的区域的个数。
SI： 是包含种子点的一幅图像。
TI： 是一幅图像，该图像中包含在经过连通性处理前通过阈值测试的像素，即具有灰度z_i且满足|z_i - S| ≤T的点。
SI和TI的大小均与f相同

regiongrow.m

function [g,NR,SI,TI]=regiongrow(f,S,T)
%regiongrow执行区域生长
f=double(f);
%如果S是标量，则包含种子图像。
if numel(S)==1
    SI=f==S;
    S1=S;
else
    %S是一个数组。排除重复，在以下编码部分，连接种子位置去减少循环执行数量。
    SI=bwmorph(3,'shrink',Inf);
    J=find(SI);
    S1 = f(J);   % 种子数组的值
end

TI=false(size(f));
for K=1:length(S1)
    seedvalue=S1(K);
    S=abs(f-seedvalue)<=T;
    TI=TI|S;
end
%使用SI的函数重构作为标记图像去获得与S中每个种子对应的区域
%函数bwlabel给每个连接区域分配不同的整数
[g,NR]=bwlabel(imreconstruct(SI,TI));

示例：区域生长对焊接孔隙检测
初始种子点：已知焊缝缺陷区域中的一些像素往往有最大的数字值（该情况下是255）

f = imread('defective_weld.tif');
[g,NR,SI,TI]=regiongrow(f,255,65);  %种子的像素值为255，65为阈值
figure;
subplot(2,2,1); imshow(f); title('原始图像');
subplot(2,2,2); imshow(SI); title('种子点的图像');
subplot(2,2,3); imshow(TI); title('所有通过阈值测试的像素');
subplot(2,2,4); imshow(g); title('对所有连接到种子点的像素进行8连通分析后的结果');

4.2 区域分裂与聚合

将一幅图像细分为一组任意的不相交区域，然后聚合和/或分裂这些区域。
令R表示整幅图像区域，选择一个属性Q，对R进行分割就是依次将它细分为越来越小的四象限区域，以便任何区域R_i都有Q（R_i） = TRUE。
从整个区域开始，若Q（R） = FALSE，则将其分割为4个象限区域，若分割后象限区域Q依旧为FALSE，则将对应的象限再次细分为四个子象限区域，以此类推。分割的过程可以用一个四叉树形式直观的表示。
细分完成后，对满足属性Q的组合像素的邻接区域进行聚合，即Q（R_j∪R_k） = TRUE时，对两区域进行聚合。

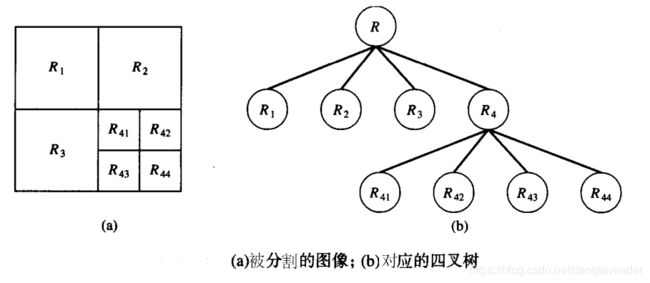
算法小结：
1、把满足Q（R_i） = FALSE的任何区域R_i分裂为4个不相交的象限区域；
2、不可能进一步分裂时，对满足条件Q（R_j∪R_k） = TRUE的任意两个邻接区域R_j和R_k进行聚；
3、无法进一步聚合时，停止操作。
习惯上要规定一个不能再进一步执行分裂的最小四象限区的尺寸。

实现
使用函数qtdecomp 进行四叉树分解的操作

S = qtdecomp(I,threshold,[mindim maxdim])
I：输入的灰度图像
threshold：分割成的子块中允许的阈值，默认为0。如果子块中最大元素和最小元素的差值小于该阈值，就认为该子块在属性Q上为TRUE，即不再进行进一步细分。对double型矩阵，threshold将直接作为阈值，而对uint8和uint16类型的矩阵，threshold将被乘以255和65535以作为实际的阈值。对图像而言，threshold的取值范围时0-1。
[mindim maxdim]：尺度阈值。mindim可屏蔽函数对尺度上小于mindim的子块的处理，不管该子块在属性Q上是否为真；若参数为[mindim maxdim]，则表示不产生小于mindim尺度的子块，也不保留大于mixdim尺度的子块。maxdim/mindim必须是2的整数次幂
S：一个稀疏矩阵，在每个子块的左上角给出了子块的大小

用一个小例子来说明一下四叉树分解结果矩阵S

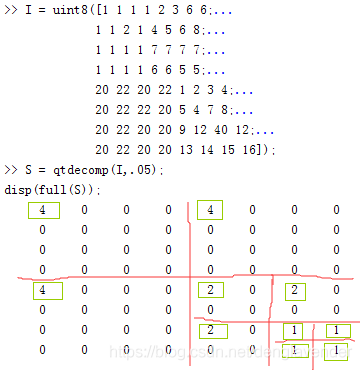
红线分割开的就是对原图像分裂得到的子块，绿色框出每个块中左上角的非零元素就是块的大小。
注： qtdecomp函数主要适用于边长是2的整数次幂的正方形图像；对长宽不是2的整数次幂的图像，分解可能无法进行到底。
为了在四叉树分解后得到指定大小子块的像素及位置信息，使用函数qtgetblk：

[vals,r,c] = qtgetblk(I,S,dim)  
I：输入的灰度图像
z：由qtdecomp返回的稀疏矩阵
dim：指定的子块大小
vals：dim*dim*k的三维矩阵，包含I中所有符合条件的子块数据。其中k为符合条件的dim*dim大小的子块的个数，vals(:,:,i)表示符合条件的第i个子块的具体内容。
r和c：均为列向量，分别表示图像I中符合条件子块左上角的行索引和列索引

同样，用一个小例子来直观的感受一下

>> I = [1    1    1    1    2    3    6    6
     1    1    2    1    4    5    6    8
     1    1    1    1   10   15    7    7
     1    1    1    1   20   25    7    7
    20   22   20   22    1    2    3    4
    20   22   22   20    5    6    7    8
    20   22   20   20    9   10   11   12
    22   22   20   20   13   14   15   16];
>> S = qtdecomp(I,5);  % 对double类型的数据，5可以直接作为阈值
>> [vals,r,c] = qtgetblk(I,S,4);  %  得到所有符合条件的大小为4*4的子块数据
>> k = size(vals,3)   %  k为符合条件的子块的个数
k =
     2
>> % 显示第一个子块的数据
>> vals(:,:,1)
ans =
     1     1     1     1
     1     1     2     1
     1     1     1     1
     1     1     1     1
>> % 显示第二个子块的数据
>> vals(:,:,2)
ans =
    20    22    20    22
    20    22    22    20
    20    22    20    20
    22    22    20    20

使用qtsetblk函数将四叉树分解所得到的的子块中符合条件的部分全部替换为指定的子块
参考：qtsetblk函数

J = qtsetblk(I,S,dim,vals)
I：输入的灰度图像
S：I经过qtdecomp函数返回的稀疏矩阵
dim：指定的子块大小
vals：dim*dim*k的三维矩阵，包含了用来替换原有子块的新子块信息。k为图像I中大小为dim*dim的子块的总数，vals(:,:,i)表示要替换的第i个子块。
J：经过子块替换的新图像

用小例子进行直观感受：

>> I = [1    1    1    1    2    3    6    6
     1    1    2    1    4    5    6    8
     1    1    1    1   10   15    7    7
     1    1    1    1   20   25    7    7
    20   22   20   22    1    2    3    4
    20   22   22   20    5    6    7    8
    20   22   20   20    9   10   11   12
    22   22   20   20   13   14   15   16];
>> S = qtdecomp(I,5);
>> vals = qtgetblk(I,S,4);
>> newvals = cat(3,zeros(4),ones(4));  % cai将矩阵合成三维，第一层为zeros(4)，第二层为ones(4)
>> J = qtsetblk(I,S,4,newvals)
J =
     0     0     0     0     2     3     6     6
     0     0     0     0     4     5     6     8
     0     0     0     0    10    15     7     7
     0     0     0     0    20    25     7     7
     1     1     1     1     1     2     3     4
     1     1     1     1     5     6     7     8
     1     1     1     1     9    10    11    12
     1     1     1     1    13    14    15    16

由结果可以明显的看出，对原图像中大小为4*4的所有子块进行的替换。
注： size(newvals,3)必须和I中指定大小的子块的数目相同，否则会出错。

示例：对图像进行四叉树分解，并以图像形式显示得到的稀疏矩阵。

I = imread('rice.tif');
I1 = imresize(I,[512,512]);  % 改变原图的大小
S = qtdecomp(I1,0.1);
S1 = full(S);  % 将稀疏矩阵转换为普通矩阵

figure;
subplot(1,3,1); imshow(I); title('原图')
subplot(1,3,2); imshow(I1); title('改变原图的大小');
subplot(1,3,3); imshow(S1); title('四叉树分解结果');

由于原图的大小为257257,直接对原图使用qtdecomp函数进行分解会报错，如下：

尝试将原图的大小修改为2的幂次，如代码中的512512，经测试，将阈值设置为0.1能得到较好的分割效果。

五、用形态学分水岭的分割

分水岭算法（watershed）是一种借鉴了形态学理论的分割方法，在该方法中，将一幅图像看成一个拓扑地形图，其中图像的灰度值对应地形高度值。高灰度值对应山峰，低灰度值对应山谷。水总是朝地势低的地方流动，直到某一局部低洼处才停下来，这个低洼处被称为汇水盆地。最终所有的水会分聚在不同的汇水盆地，汇水盆地之间的山脊被称为分水岭。对图像进行分割，就是要在灰度图像中找出不同的“汇水盆地”和“分水岭”。也就是感兴趣的区域内部及其边缘。

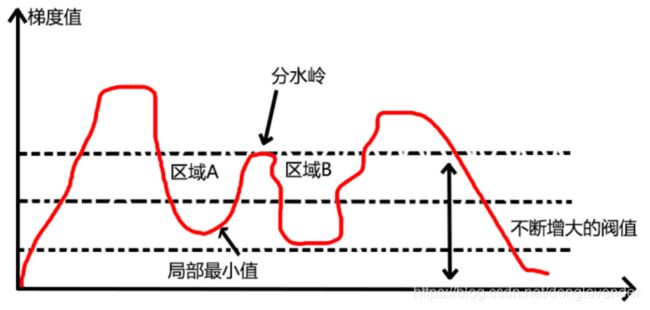
一般考虑到各区域内部像素的灰度比较接近，而相邻区域像素间的灰度差距较大，可以先计算一幅图像的梯度图，再寻找梯度图的分水岭。在梯度图中，小梯度值对应区域内部，大梯度值对应区域的边界，分水岭算法就是在寻找大梯度值像素的位置。

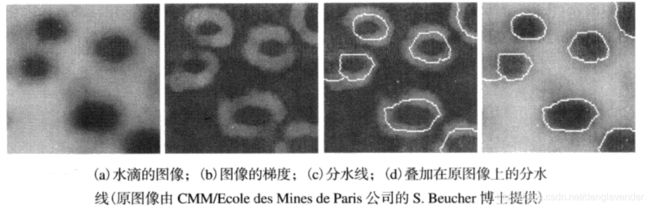
直接应用分水岭分割算法的效果往往并不好，通常会由于噪声和梯度的其他局部不规则性造成过度分割。更有甚者，过度分割可能导致不可用的结果。一种解决方案是，通过融入预处理步骤来限制允许存在的区域数量。
用于控制过度分割的一种方法是基于标记的。标记是指属于一幅图像的连通分量。与感兴趣物体相联系的标记称为内部标记，与背景相关联的标记称为外部标记。

实现

有关计算梯度图像的简单说明：以sobel算子为例

f = imread('gel-image.tif');
h=fspecial('sobel');
fd=double(f);
g=sqrt(imfilter(fd,h,'replicate').^2+imfilter(fd,h','replicate').^2);
g1 = imgradient(f); % 使用imgradient函数也可直接得到图像的梯度
g2 = imcomplement(imsubtract(g,g1));
figure;
subplot(2,2,1); imshow(f); title('原图');
subplot(2,2,2); imshow(g,[]); title('用sobel算子计算图像梯度')
subplot(2,2,3); imshow(g1,[]); title('用imgradient函数计算图像梯度')
subplot(2,2,4); imshow(g2,[]); title('两种计算梯度方法的差值');

1、计算梯度可以使用sobel算子，然后分别求水平方向和竖直方向的偏导数，再计算梯度；也可以使用imgradient函数直接得到图像的梯度。
2、用sobel算子计算梯度时，首先要将原图像转换为double类型，因为sqrt函数不支持uint8类型（用imread函数读入的图像为uint8类型）；imgradient函数可直接对uint8类型图像进行处理，也可处理double类型图像
3、将用两种方法得到的梯度图像相减，从图中可以看出效果是一样的。

参考：标记控制的分水岭分割
watershed函数——对图像进行分水岭算法处理，调用格式如下：

L = watershed(A)
或  L = watershed(I,conn)
I：输入的需要处理的原图像
conn：可选参数，用于指定分水岭算法将要考虑的邻域数量。对于二维图像，这个值可以为4或者8，该函数也可以处理三维图像。
L：输出的矩阵中数值为0的元素表明不属于任何一个划分出的区域，而各个分水岭分割出的区域被用不同的序号表示，输出的矩阵时double类型 。

imregionalmin函数——计算图像中大量局部最小区域的位置，调用格式如下：

rm = imregionalmin(f)
f：灰度图像
rm：二值图像，二值图像的前景像素标记了局部最小区域的位置。

imextendedmin函数——扩展最小值变换，即计算图像中比周围点更深的点的集合（通过某个高度阈值）。调用格式如下：

im = imextendedmin(f,h)
f：灰度图像
h：高度阈值
im：是一个二值图像，该二值图像的前景像素编辑了深局部最小值区域的位置。

示例：控制标记符的分水岭分割

f = imread('gel-image.tif');
h=fspecial('sobel');
fd=double(f);
g=sqrt(imfilter(fd,h,'replicate').^2+imfilter(fd,h','replicate').^2);
L=watershed(g);
wr=L==0;  % L的0值像素是分水岭脊像素

% 基于梯度图像进行分水岭变换，会看到由大量局部最小区域导致的过度分割
rm=imregionalmin(g); % 计算图像中所有的局部小区域的位置
im=imextendedmin(f,2); % 扩展极小值变换，用于计算比周围点更暗的图像中“低点”的集合
fim=f;
fim(im)=175;  % 上两行将在原图像上以灰色气泡的形式叠加扩展的局部最小区域位置

Lim=watershed(bwdist(im));  % 通过计算内部标记符图像im的距离变换分水岭可以得到外部标记
em=Lim==0;
g2=imimposemin(g,im | em); % 使用 imimposemin 来修正梯度幅值图像，使其局部最小值只出现在前景和背景标记像素上。
L2=watershed(g2);
f2=f;
f2(L2==0)=255;

figure;
subplot(2,4,1); imshow(f); title('原图');
subplot(2,4,2); imshow(wr,[]);title('(a)梯度幅度图像进行分水岭变换图像');
subplot(2,4,3); imshow(rm,[]);title('(b)对梯度幅度图像的局部最小区域');
subplot(2,4,4); imshow(fim,[]);title('(c)内部标记符');
subplot(2,4,5); imshow(em,[]);title('(d)外部标记符');
subplot(2,4,6); imshow(g2,[]);title('(e)修改后的梯度幅度值图像');
subplot(2,4,7); imshow(f2),title('(f)最后分割的结果');