PCA求解思路
学习完了NG的PCA和《机器学习实战》的PCA
有一点很疑惑不解,对矩阵A,
NG是先用A - Amean,然后求协方差矩阵 covA = 1/m * AT * A 然后进行SVD分解,得到 U
因为 1/m*( AT * A) = V * (lambda**2/m) * VT ,所以其实就是求出对A进行SVD分解的V
《实战》是用A - Amean, 然后求协方差矩阵 covA = 1/m * AT *A 然后求特征值和特征向量
也就是对A进行 SVD分解之后得到的V
那么问题就来了,为什么一定要求协方差矩阵,而不是直接对A进行SVD分解得到V呢?
想太多也没有用,直接来实践吧,直接修改《实战》中的代码
原代码:
def pca(dataMat, topNfeat = 9999999):
meanVals = mean(dataMat, axis = 0)
meanRemoved = dataMat - meanVals
#covariance matrix, x.T * x
#If rowvar is True (default), then each row represents a variable, with observations in the columns
covMat = cov(meanRemoved, rowvar = False)
#Compute the eigenvalues and right eigenvectors of a square array.
eigVals,eigVects = linalg.eig(mat(covMat))
#Returns the indices that would sort an array.
eigValInd = argsort(eigVals)
eigValInd = eigValInd[:-(topNfeat + 1):-1]
redEigVects = eigVects[:,eigValInd]
lowDDataMat = meanRemoved * redEigVects
reconMat = (lowDDataMat * redEigVects.T) + meanVals
return lowDDataMat, reconMat
修改后的代码:
def pca(dataMat, topNfeat = 9999999):
meanVals = mean(dataMat, axis = 0)
meanRemoved = dataMat - meanVals
#covariance matrix, x.T * x
#If rowvar is True (default), then each row represents a variable, with observations in the columns
#covMat = cov(meanRemoved, rowvar = False)
#Compute the eigenvalues and right eigenvectors of a square array.
#eigVals,eigVects = linalg.eig(mat(covMat))
#Returns the indices that would sort an array.
s,eigVals,d = linalg.svd(meanRemoved)
eigVects = d.T
eigValInd = argsort(eigVals)
eigValInd = eigValInd[:-(topNfeat + 1):-1]
redEigVects = eigVects[:,eigValInd]
lowDDataMat = meanRemoved * redEigVects
reconMat = (lowDDataMat * redEigVects.T) + meanVals
return lowDDataMat, reconMat
只有一点点小改动,就是不求协方差矩阵,而是直接对减去平均值之后的矩阵进行SVD分解,然后求出V
然后得出的结果,一模一样
然后更改《实战》里查看特征值的代码
不求协方差矩阵,而是直接对减去平均值之后的矩阵进行SVD分解,然后查看lambda
记住协方差矩阵的特征值为lambda**2/m
所以我们对求得的lambda先平方,再除以样本的数目,得出的结果。。仍然是一模一样
也就是说,按照我的推论,不求协方差矩阵,而是直接对减去平均值之后的矩阵进行SVD分解,然后求出V,这样的推论是合理的。
如果有不对的地方,请大家回复一下帮我改正,感谢。
**************************************************************************分割线********************************************************************************
因为尝试了可以直接对减去平均值之后的矩阵进行SVD分解,然后求出V
又因为不理解PCA的本质,所以尝试了不减去平均值,直接对原矩阵进行SVD分解,
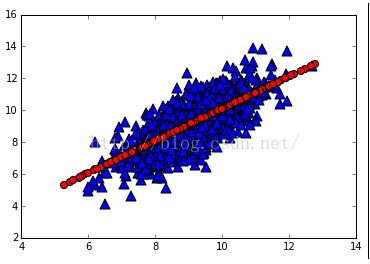
得出的结果如下
(查了资料,这样的效果并不好,因为PCA寻找的是“保留更多信息的维度”,也就是说在这个维度的投影尽量分散,如果不先求均值的话,就达不到分散的效果。。这样求的是过原点的尽量分散的维度。这并不符合我们的目的),更新,这一段是错误的,如果这样的话,得到的只会是过原点的一条直线,这样不行,我们需要得到的数据,是一条有斜率并且有偏置的线/面,并不是一条过原点的线/面。
更详细的理解:
http://www.360doc.com/content/13/1124/02/9482_331688889.shtml
TruncatedSVD is very similar to PCA, but differs in that it works on sample matrices directly instead of their covariance matrices. When the columnwise (per-feature) means of are subtracted from the feature values, truncated SVD on the resulting matrix is equivalent to PCA.