一中OJ #1480 相似基因 | 动态规划 序列匹配 | 解题报告
一中OJ | #1480 相似基因 | 匹配型动态规划
时限 1000MS/Case 内存 64MB/Case
题目描述
大家都知道,基因可以看作一个碱基对序列。它包含了4种核苷酸,简记作A,C,G,T。生物学家正致力于寻找人类基因的功能,以利用于诊断疾病和发明药物。在一个人类基因工作组的任务中,生物学家研究的是:两个基因的相似程度。因为这个研究对疾病的治疗有着非同寻常的作用。两个基因的相似度的计算方法如下:
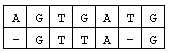
对于两个已知基因,例如AGTGATG和GTTAG,将它们的碱基互相对应。当然,中间可以加入一些空碱基-,例如:
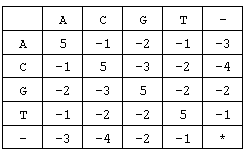
这样,两个基因之间的相似度就可以用碱基之间相似度的总和来描述,碱基之间的相似度如下表所示:
那么相似度就是:(-3)+5+5+(-2)+(-3)+5+(-3)+5=9。
因为两个基因的对应方法不唯一,例如又有:
相似度为:(-3)+5+5+(-2)+5+(-1)+5=14。
规定两个基因的相似度为所有对应方法中,相似度最大的那个。
输入格式
共两行。每行首先是一个整数,表示基因的长度;隔一个空格后是一个基因序列,序列中只含A,C,G,T四个字母。1<=序列的长度<=100。
输出格式
仅一行,即输入基因的相似度。
样例输入
7 AGTGATG
5 GTTAG
样例输出
14
数据范围
1<=序列的长度<=100。
----------------------------------------------------------
题目分析
此题重点在于方程的设计以及转移。要求序列1与序列2匹配得到的最大的相似度,那么则逐个考察序列1与序列2的某个位置的匹配是否合适
与一般的匹配方程不同,此题在转移方程中要考虑添加空碱基的情况
设f[i][j]为考察到序列1的位置i和序列2的位置j能得到的最大相似度,矩阵a[][]为对应碱基的相似度
那么转移状态如下:
1.序列1的i与序列2的j匹配,那么f[i][j]=f[i-1][j-1]+a[x[i]][y[j]]
2.序列1的i与序列2的空碱基匹配,那么f[i][j]=f[i-1][j]+a[x[i]][空]
3.序列1的空碱基与序列2的j匹配,那么f[i][j]=f[i][j-1]+a[y[j]][空]
4.没有序列1的空碱基与序列2的空碱基匹配的情况
总的状态转移方程就是上面三个取max
在完成程序时,可以先将碱基转换为数字作为下标
关于初始值的设计,f[0][0]=0,{f[i][j] | 1<= i <=maxlen} =-inf是肯定的,重点在于{f[i][0],f[0][j] | 1<= i <=maxlen}=对应i或j位置与空碱基的匹配值(特判),为什么呢?因为f[i][0]与f[0][j]就是对应位置与空碱基的匹配啊
----------------------------------------------------------
代码
#include
#include
#include
#include
#include
#include
#include
#include