【动态规划】树形dp

概念理解：

• 我们学过的一般DP方程一般都是一维或者二维的，而数组是一种线性结构，具有很强的位置关系限制(一个挨着一个)，所以一般在线性结构上的dp都很容易计算

• 然而除了线性的数据结构之外，还有很多非线性的数据结构，最典型的就是树。

• 由于树本身的特殊性质，树的局部性体现在其递归结构上：即以一个节点为根的子树是由它儿子的子树组成的，所以我们在解决树形DP问题的时候一般是选择按照层数从底向上，也就是对于每个节点，用其它节点的子树答案计算出它的子树答案。

特点解说:

• 我们设置状态时也一般第一个是设置根，这样也可以用递归转移。

• 因为树形dp是具有层次型的dp，所以我们实现dp时一般采用dfs递归更新，也就是信息界人称的“记忆化搜索”。

• 树形dp因为是一张图，所以我们一般用邻接表或者vector来存储点与点之间的关系。

例题：

一、联合权值

题目描述：
无向连通图 G 有 n 个点，n−1 条边。点从 1 到 n 依次编号,编号为 i 的点的权值为 Wi，每条边的长度均为 1。图上两点 (u,v) 的距离定义为 u 点到 v 点的最短距离。对于图 G 上的点对 (u,v)，若它们的距离为 2，则它们之间会产生Wv×Wu​ 的联合权值。
请问图 G 上所有可产生联合权值的有序点对中，联合权值最大的是多少？所有联合权值之和是多少？

---

输入输出格式

输入格式：
第一行包含 1 个整数 n。
接下来 n−1 行,每行包含 2 个用空格隔开的正整数 u,v，表示编号为 u 和编号为 v 的点之间有边相连。
最后 1 行,包含 n 个正整数，每两个正整数之间用一个空格隔开，其中第 i 个整数表示图 G 上编号为 i 的点的权值为 Wi。

---

输出格式：
输出共 1 行,包含 2 个整数，之间用一个空格隔开,依次为图 G 上联合权值的最大值和所有联合权值之和。由于所有联合权值之和可能很大，输出它时要对10007取余。

---

分析：因为题目说两个点之间的距离为2就是一个有序数对，所以我们就可以知道一对有序序对之间必定隔着一个中转点 例如下图：
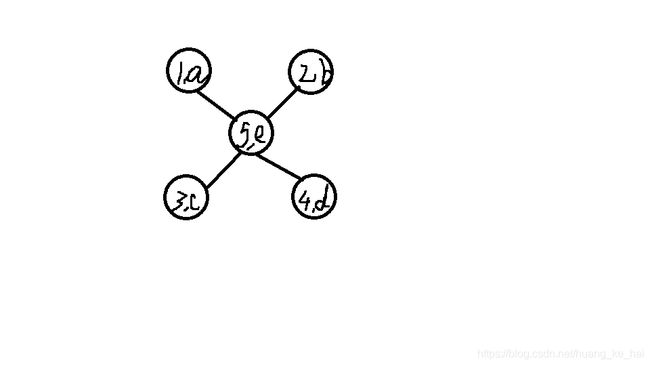其中1、2、3、4互为序对，因为它们都隔着一个中转点5，它们之间的距离都为2，所以做这道题的基础就是枚举中转点，它延伸出去的点必定互为序对。

那么枚举的问题解决了，这回我们就需要想算的问题。
第一个求最大值很好理解，我们只需要枚举中间点，在枚举它延伸出去的点，然后找一个最大值和次大值就可以了。
例如上图中的最大值就是 c*d=12;

第二个问题需要用到乘法的一些定则。
举个例子：
上图的和为$$a\ast b+a\ast c+a\ast d+b\ast a+b\ast c+b\ast d+c\ast a+c\ast b+c\ast d+d\ast a+d\ast c+d\ast b$$
经过整理可以变成：
$$（a\ast b+a\ast c+a\ast d+b\ast c+b\ast d+c\ast d）\ast 2$$
再经过整理可以变成：
$$（a\ast (b+c+d)+b\ast (c+d)+c\ast d）\ast 2$$
所以我们发现求和只需要用一个sum记录前几个数求得的和，然后不停的用后面的数累乘即可，具体的证明可以用乘法分配律展开求得。

不过求得后最后的乘2不能忘掉，这也是一个坑点。

那么具体代码如下：

#include
using namespace std;
#define P 10007
struct node{
    int next,y;
}e[1000001];
int v[1000001];
int n;
int linkk[10000001];
int len;
void insert(int xx,int yy){
    e[++len].next=linkk[xx];
    linkk[xx]=len;
    e[len].y=yy;
}
int main(){
    scanf("%d",&n);
    for (int i=1,x,y;i<n;i++) scanf("%d %d",&x,&y),insert(x,y),insert(y,x);
    int ans=0,maxx=0;
    for (int i=1;i<=n;i++) scanf("%d",&v[i]);
    for (int i=1;i<=n;i++){
    	int max1=0,max2=0,sum=0;
	    int t=linkk[i];
	    for (int j=t;j;j=e[j].next){
		    if (v[e[j].y]>max1) max2=max1,max1=v[e[j].y];
		    else max2=max(max2,v[e[j].y]);
		    ans=(ans+sum*v[e[j].y])%P;
		    sum=(sum+v[e[j].y])%P;
		}
		maxx=max(maxx,max1*max2);
	}
	printf("%d %d",maxx,(ans*2)%P);
	return 0;
}

大家别介意。。这道题的分析跟我写的博客一模一样。。不过我觉得我分析的还是挺到位的。（假的。）

二、战略游戏

题目描述：
Bob喜欢玩电脑游戏，特别是战略游戏。但是他经常无法找到快速玩过游戏的办法。现在他有个问题。他要建立一个古城堡，城堡中的路形成一棵树。他要在这棵树的结点上放置最少数目的士兵，使得这些士兵能了望到所有的路。注意，某个士兵在一个结点上时，与该结点相连的所有边将都可以被了望到。
请你编一程序，给定一树，帮Bob计算出他需要放置最少的士兵。

---

输入格式
输入文件中数据表示一棵树，描述如下： 第一行 N，表示树中结点的数目。 第二行至第N+1行，每行描述每个结点信息，依次为：该结点标号i，k(后面有k条边与结点I相连)，接下来k个数，分别是每条边的另一个结点标号r1，r2，…，rk。 对于一个n(0

---

输出格式
输出文件仅包含一个数，为所求的最少的士兵数目。

---

分析：这是一道经典的树形dp问题。我们设:
$dp[i][0]$表示以i为根的子树的所有节点都能被瞭望到，第i个位置不放士兵的最小值
$dp[i][1]$表示以i为根的子树的所有节点都能被瞭望到，第i个位置放士兵的最小值

不难发现，如果dp[i][0]不放士兵，那么它的儿子必定是要放士兵的，只有这样才能满足所有的东西都被瞭望到。
转移方程如下：

$$\sum _{j\in son(i)}dp[i][0]+=dp[j][1]$$

如果第i个点放士兵，那么它的儿子节点士兵可放可不放，两个取一个较小值即可

转移方程如下：
$$\sum _{j\in son(i)}dp[i][1]+=min(dp[j][0],dp[j][1])+1$$

具体操作需要在图上完成，只需要开一个vector建立图然后在递归完成转移即可。

那么具体代码如下：

#include
using namespace std;
int dp[2001][2];
vector < int > e[1000011];
int n;
int vis[1100001];
void Dp(int x){
    dp[x][0]=0;
    dp[x][1]=1;
    for (int i=0;i<e[x].size();i++){
	    int y=e[x][i];
	    Dp(y);
	    dp[x][0]+=dp[y][1];
	    dp[x][1]+=min(dp[y][0],dp[y][1]);
	}
}
int main(){
    scanf("%d",&n);
    for (int i=1;i<=n;i++){
	    int x,m;
	    scanf("%d %d",&x,&m);
	    for (int j=1,y;j<=m;j++) scanf("%d",&y),vis[y]=1,e[x].push_back(y)/*,e[y].push_back(x)*/;
	}
	int rot;
	for (int i=0;i<n;i++) if (!vis[i]){
	    rot=i;break;
	}
	Dp(rot);
	printf("%d",min(dp[rot][0],dp[rot][1]));
	fclose(stdin);
	fclose(stdout);
	return 0;
}

三、最大利润

题目描述： 政府邀请了你在火车站开饭店，但不允许同时在两个相连接的火车站开。
任意两个火车站有且只有一条路径，每个火车站最多有50个和它相连接的火车站。
告诉你每个火车站的利润，问你可以获得的最大利润为多少。

---

输入格式
第一行输入整数N(<=100000)，表示有N个火车站，分别用1，2。。。，N来编号。
接下来N行，每行一个整数表示每个站点的利润，接下来N-1行描述火车站网络，每行两个整数，表示相连接的两个站点。

---

输出格式
输出一个整数表示可以获得的最大利润。

---

分析：这题就是战略游戏的一个加权版。我们只要将战略游戏的+1改为+它的利润就可以了。不过需要注意的是因为一个地方被建立了商店之后与他相邻的商店都不能建立，所以只需要将转移方程稍微修改一下就可以了

那么具体代码如下：

#include
using namespace std;
int v[1000001];
vector < int > e[1000001];
int n;
bool vis[1000001];
int dp[1000001][2];
void Dp(int x){
	vis[x]=1;
    dp[x][0]=0;
    dp[x][1]=v[x];
    for (int i=0;i<e[x].size();i++){
	    int y=e[x][i];
	    if (vis[y]) continue;
	    Dp(y);
	    dp[x][0]+=max(dp[y][1],dp[y][0]);
	    dp[x][1]+=dp[y][0];
	}
}
int main(){
	freopen("profit.in","r",stdin);
	freopen("profit.out","w",stdout);
    scanf("%d",&n);
    for (int i=1;i<=n;i++)scanf("%d",&v[i]);
    for (int i=1,x,y;i<n;i++) scanf("%d %d",&x,&y),e[x].push_back(y),e[y].push_back(x);
	Dp(1);
	printf("%d",max(dp[1][0],dp[1][1]));
	fclose(stdin);
	fclose(stdout);
	return 0;
} 

如果你们想写状压，请去这里
如果你们有兴趣去看我的其它博客，请看这里