大数因数分解Pollard_rho 算法详解
适用范围:给你一个大数n,将它分解它的质因子的乘积的形式。
P.S. 在下面的论述中会使用到Miller_rabin和快速乘法和快速幂,如果有兴趣请看另一篇博文。
不过其实你只需要知道Miller_rabin是判断一个数是否是素数。q_mul是求(a*b)% mod,q_pow是求(a^b) % mod即可。
Miller_rabin素数判断:http://blog.csdn.net/maxichu/article/details/45458569
大数分解最简单的思想也是试除法,这里就不再展示代码了,就是从2到sqrt(n),一个一个的试验,直到除到1或者循环完,最后判断一下是否已经除到1了即可。
但是这样的做的复杂度是相当高的。一种很妙的思路是找到一个因子(不一定是质因子),然后再一路分解下去。这就是基于Miller_rabin的大数分解法Pollard_rho大数分解。
Pollard_rho算法的大致流程是 先判断当前数是否是素数(Miller_rabin)了,如果是则直接返回。如果不是素数的话,试图找到当前数的一个因子(可以不是质因子)。然后递归对该因子和约去这个因子的另一个因子进行分解。
那么自然的疑问就是,怎么找到当前数n的一个因子?当然不是一个一个慢慢试验,而是一种神奇的想法。其实这个找因子的过程我理解的不是非常透彻,感觉还是有一点儿试的意味,但不是盲目的枚举,而是一种随机化算法。我们假设要找的因子为p,他是随机取一个x1,由x1构造x2,使得{p可以整除x1-x2 && x1-x2不能整除n}则p=gcd(x1-x2,n),结果可能是1也可能不是1。如果不是1就找寻成功了一个因子,返回因子;如果是1就寻找失败,那么我们就要不断调整x2,具体的办法通常是x2=x2*x2+c(c是自己定的)直到出现x2出现了循环==x1了表示x1选取失败重新选取x1重复上述过程。(似乎还存在一个每次找寻范围*2的优化,但是不太懂。。。)
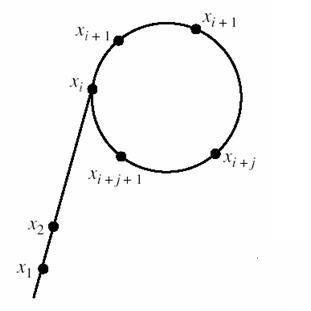
因为x1和x2再调整时最终一定会出现循环,形成一个类似希腊字母rho的形状,故因此得名。
另外通过find函数来分解素数,如果找到了一个素数因子则加入到因子map中,否则如果用Pollard找到一个因子则递归去找素数因子。
上代码:
#include
#include
#include
#include
#include
#include
