QR分解求矩阵绝对值-基于HouseHolder变换
输入矩阵A(mxn)——>HouseHolder变换——>获得矩阵B(Hessenberg矩阵nxn)——>Gievens变换
——>获得Q(标准正交nxn)和R(上三角nxn)——>更新B(R*Q)——>将B带入Givens变换迭代
——>更新B(R*Q)——>重复一定次数(特征值逼近)——>B的主对角线元素就是矩阵A的全部特征值(近似值)
关于HouseHolder、Givens变换的介绍不再重复,只列出对应的算法
算法:
HouseHolder:
A = |aij| 1<=i<=m 1<=j<=n 1<=col<=n-2
X = |xi|; if(i>col) xi = a(i,col); if(i<=col) xi = 0;
W = |wi|; if(i~=col+1) wi = 0; if(i==col+1) wi = ||x||(长度)
V = w + sign(x0)*X; if(x0<=0) sign(x0) = 1; if(x0>0) sign(x0) = -1
P = V'*V/V*V'(nxn向量除以一个数值)
Hcol = I-2*P (第col阶HouseHolder矩阵)
迭代:Hn-2*...*Hcol*...*H2*H1*A*H1*H2*...*Hcol*...Hn-2
矩阵A有m行n列,col是迭代次数1~n-2,Hcol是col阶HouseHolder矩阵
Givens:
B = H_Hess = |bij| 1<=i,j<=n 1<=k<=n-1
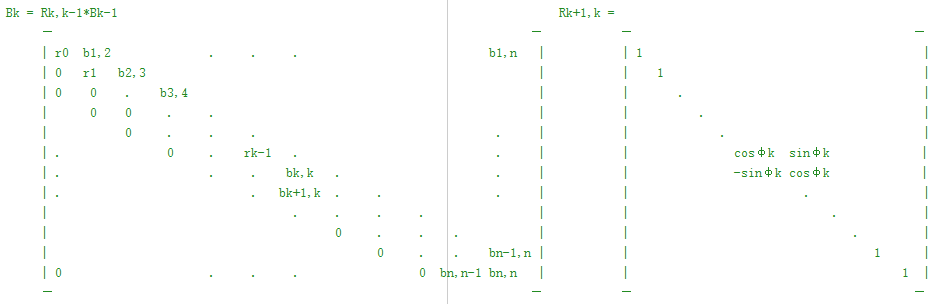
Givens变换:cosφk = bk,k/rk sinφk = bk+1,k/rk rk = sqrt(bk,k^2+bk+1,k^2)
迭代-1:R = Rn,n-1*...*Rk+1,k*...*R3,2*R2,1*B1 Q = Rn,n-1*...*Rk+1,k*...*R3,2*R2,1
迭代-2:设定B_delt或迭代次数 B = RQ
获得主对角线元素作为全部特征值
cosφk在Rk+1,k的第k行k列;迭代-2:将B带入Givens变换执行迭代-1获得Q、R,让B=RQ重复带入Givens变换
MATLAB仿真:
HouseHolder部分:
function A_Hess = HouseHolder_Hessenberg(A)
A = [5 -3 2;6 -4 4;4 -4 5];
%把输入矩阵转成Hessenberg矩阵
[m,n] = size(A);
X = zeros(1,m);
W = zeros(1,m);
A_Hess = A;
for col = 1:n-2
for i = 1:m
if(i<=col)
X(i) = 0;
else
X(i) = A(i,col);
end
end
X_sq = X*X';
X_len = sqrt(X_sq); %求X长度
for i = 1:m
if(i~=col+1)
W(i) = 0;
else
W(i) = X_len;
end
end
V = W+X;
P = (V'*V)./(V*V');
H_col = eye(n)-2*P;
A_Hess = H_col*A_Hess*H_col;
end
Givens部分:
%function lambda = QR_HS(A) 输出绝对值序列
clc;
close all;
clear all;
A = [5 -3 2;6 -4 4;4 -4 5]; %测试矩阵
B = HouseHolder_Hessenberg(A); %返回Hessenberg矩阵
n = size(B,1);
Q = eye(n);
%迭代20次
%Givens变换
for i = 1:20
for k = 1:n-1r_k = sqrt(B(k,k)^2+B(k+1,k)^2);
cos_phi_k = B(k,k)/r_k;
sin_phi_k = B(k+1,k)/r_k;
R_k = eye(n);
R_k(k,k) = cos_phi_k;
R_k(k,k+1) = sin_phi_k;
R_k(k+1,k) = -sin_phi_k;
R_k(k+1,k+1) = cos_phi_k;
B = R_k*B; %更新B
Q = Q*R_k'; %获得标准正定矩阵
R = B;%获得上三角矩阵
end
B = R*Q %获得新矩阵B用于下次迭代
Q = eye(n);%清零
end
%输出绝对值序列
lambda = zeros(1,n);
for i = 1:n
lambda(1,i) = B(i,i);
end
测试输出:lambda = [2.9998 2.0002 1.0000]