最大完全子块
Description
A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles: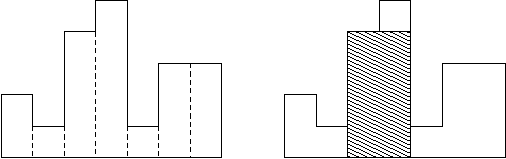
Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.
Input
The input contains several test cases. Each test case describes a histogram and starts with an integer n, denoting the number of rectangles it is composed of. You may assume that 1 <= n <= 100000. Then follow n integers h1, ..., hn, where 0 <= hi <= 1000000000. These numbers denote the heights of the rectangles of the histogram in left-to-right order. The width of each rectangle is 1. A zero follows the input for the last test case.
Output
For each test case output on a single line the area of the largest rectangle in the specified histogram. Remember that this rectangle must be aligned at the common base line.
Sample Input
7 2 1 4 5 1 3 3 4 1000 1000 1000 1000 0
Sample Output
8 4000
解析:
对于任意位置i,r[i]表示能向右延伸的最远位置,l[i]表示能向左延伸的最远位置,h[i]表示i位置的高度,
那么res=max{(r[i]-l[i])*h[i]};
如何求l[i]和r[i]是解决问题的关键,从复杂度上来看,肯定不是对于每个i都向左和向右扫一遍,在这里用到了单调栈。
AC代码:
#include
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 5;
int n;
int l[maxn], r[maxn];
ll dp[maxn], a[maxn];
int main() {
while(scanf("%d", &n) && n) {
for(int i = 1; i <= n; i++) {
scanf("%lld", a + i);
}
memset(l, 0, sizeof l);
memset(r, 0, sizeof r);
stack s1, s2;
for(int i = 1; i <= n; i++) {
while(!s1.empty() && a[s1.top()] >= a[i])
s1.pop();
if(s1.empty())
l[i] = 0;
else
l[i] = s1.top();
s1.push(i);
}
for(int i = n; i >= 1; i--) {
while(!s2.empty() && a[s2.top()] >= a[i])
s2.pop();
if(s2.empty())
r[i] = n + 1;
else
r[i] = s2.top();
s2.push(i);
}
ll res = 0;
for(int i = 1; i <= n; i++) {
res = max(res, (r[i] - l[i] - 1) * a[i]);
}
printf("%lld\n", res);
}
return 0;
} Description
Bob is a strategy game programming specialist. In his new city building game the gaming environment is as follows: a city is built up by areas, in which there are streets, trees,factories and buildings. There is still some space in the area that is unoccupied. The strategic task of his game is to win as much rent money from these free spaces. To win rent money you must erect buildings, that can only be rectangular, as long and wide as you can. Bob is trying to find a way to build the biggest possible building in each area. But he comes across some problems – he is not allowed to destroy already existing buildings, trees, factories and streets in the area he is building in.
Each area has its width and length. The area is divided into a grid of equal square units.The rent paid for each unit on which you're building stands is 3$.
Your task is to help Bob solve this problem. The whole city is divided into K areas. Each one of the areas is rectangular and has a different grid size with its own length M and width N.The existing occupied units are marked with the symbol R. The unoccupied units are marked with the symbol F.
Input
The first line of the input contains an integer K – determining the number of datasets. Next lines contain the area descriptions. One description is defined in the following way: The first line contains two integers-area length M<=1000 and width N<=1000, separated by a blank space. The next M lines contain N symbols that mark the reserved or free grid units,separated by a blank space. The symbols used are:
R – reserved unit
F – free unit
In the end of each area description there is a separating line.
Output
For each data set in the input print on a separate line, on the standard output, the integer that represents the profit obtained by erecting the largest building in the area encoded by the data set.
Sample Input
2 5 6 R F F F F F F F F F F F R R R F F F F F F F F F F F F F F F 5 5 R R R R R R R R R R R R R R R R R R R R R R R R R
Sample Output
45 0
解析:
这个题是上面那个问题的进阶版,这个题我们可以设置h[i][j],表示第i行,第j列能向上延伸的最大高度,那么这个问题就变成了i个第一个问题。
每一行用单调栈计算距离,最后取最大即可。
这个题的读入有毒,用了cin过了,网上还有其他解用的字符数进行读入配合scanf肯定是比cin要快不少。
AC代码:
#include
using namespace std;
typedef long long ll;
const int maxn = 1000 + 5;
ll h[maxn][maxn], l[maxn], r[maxn];
int n, m;
char ch;
int main() {
int t;
scanf("%d", &t);
while(t--) {
memset(h, 0, sizeof h);
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
cin >> ch;
if(ch == 'F')
h[i][j] = h[i - 1][j] + 1;
else
h[i][j] = 0;
}
}
ll res = 0;
for(int i = 1; i <= n; i++) {
memset(l, 0, sizeof l);
memset(r, 0, sizeof r);
stack s_l, s_r;
for(int j = 1; j <= m; j++) {
while(!s_l.empty() && h[i][s_l.top()] >= h[i][j])
s_l.pop();
if(s_l.empty())
l[j] = 0;
else
l[j] = s_l.top();
s_l.push(j);
}
for(int j = m; j >= 1; j--) {
while(!s_r.empty() && h[i][s_r.top()] >= h[i][j])
s_r.pop();
if(s_r.empty())
r[j] = m + 1;
else
r[j] = s_r.top();
s_r.push(j);
}
for(int j = 1; j <= m; j++) {
res = max(res, (r[j] - l[j] - 1) * h[i][j]);
}
}
printf("%lld\n", res * 3);
}
return 0;
}