『最小生成树』Kruskal算法——加边法 （并查集优化 + C++语言编写 + 例题）

『算法原理』

---

         在一个连通网的所有生成树中，各边的代价之和最小的那颗生成树称为该连通网的最小代价生成树（Minimum Cost Spanning Tree）,简称最小生成树(MST)。

        Kruskal算法之所以叫加边法，就是因为其本质是一个边一个边地加入到最小生成树中。

算法步骤如下：

设有一无向连通图G，有n个顶点。

• a.将所有边的权值从小到大排列。
• b.遍历所有的边，如果边加入生成树后不形成环，则将该边加入到生成树中
• c.重复b步骤直至所有顶点都被加入到生成树中，即生成树中加入了n-1条边

 

下面用图示来解释这个过程。

 

a.将所有的边从小到大排序

12 19 25 25 26 34 38 46  

b.遍历所有的边，如果边加入生成树后不形成环，则将该边加入到生成树中

 

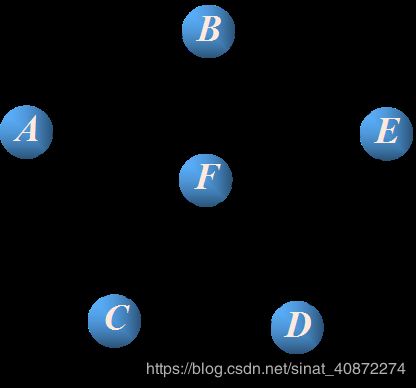
1).加入权最小的（B，E）

2).加入（C，D）

3).加入（A，F）

3).加入（C，F）

4).加入（F，D），此时发现 F C  D形成一个环，不选

5).加入（F，E） 6个点，到此加入了5条边，生成最小生成树 算法结束

在模拟之后，大家就可以发现，Kruskal算法在代码实现时的最大困难在于“如何判断是否成环”。

模拟的过程中可以发现，n个顶点在初始状态下可看成n个独立的连通块，在不断加边的过程中，边的两端点会连在一起，形成一个连通块，故边的端点在边加入前会出现两种状态

（Vi，Vj为边的两端点）

a.Vi，Vj都属于同一连通块  例：上图中，当要加入（F，D）之前，F 和 D都属于 "A-F-C-D" 这一连通块

b.Vi，Vj分别属于不同的连通块  例：上图中，当要加入（C，D）之前，C属于“C”这一连通块，D属于“D”这一连通块

可以看出 a情况下即是成环，故判断边的两端点是否都在同一个连通块中中，就是判断是否成环。

这里引入一个并查集的概念

简单来说就是在一个连通块中找出一个顶点作为“根”，同连通块的其他顶点都是“根”的孩子，如果两顶点的“根”相同，则两顶点是在同一连通块，如果A和B不在同一类中，则将B的“根”变为A的“根”的孩子就可以将A和B归在同一类。

具体的讲解，附上网上流传的一个通俗的帖子

https://blog.csdn.net/u013546077/article/details/64509038

『模板代码』

---

以上面的图为测试数据，将原图中“ABCDEF”的点编号更改为"123456";

/*****************************
*author:ccf
*source:POJ-
*topic:
*******************************/
/*

a.将所有边的权值从小到大排列。
b.遍历所有的边，如果边加入生成树后不形成环，则将权值最小的边加入到生成树中
c.重复b步骤直至所有定点都被加入到生成树中，即生成树中加入了n-1条

********************************************************
*/
#include 
#include 
#include 
#include 
#include 
using namespace std;
int f[105];
struct Edge{
	int v,u,w;//v-起点  u-终点   w-权值 
}edge[100]; 
bool cmp(const Edge& a,const Edge& b){
	return a.w < b.w;
}
void Init(){
	for(int i = 0; i <= 100; i++)
		f[i] = i;
}
int check(int a){//用于查找到a的"祖先" 并返回 
	if(f[a] == a)
		return a;
	else{
		f[a] = check(f[a]);
	}
	return f[a];
}
bool merger(int a,int b){//将a和b归并到同一"根"下 
	int t1 = check(a),t2 = check(b);//先找到a和b的根 t1，t2；
	if(t1 == t2){//如果a和b的"根"一样 成环 返回错误
		return false;
	}else{
		f[t2] = f[t1];//如果a和b的"根"不一样 ，不成环，将a，b归在同一个"根"下 
		return true; 
	}
}
int main(){
	int n,tot = 0,sum = 0;
	cin>>n;
	int a,b,c;
	Init();
	for(int i = 1; i <= n; i++){
		cin>>a>>b>>c;
		edge[i].v = a;
		edge[i].u = b;
		edge[i].w = c;
	}
	sort(edge+1,edge+n+1,cmp);//a.将所有边的权值从小到大排列。
	cout<<"权值从小到大排列序列如下：\n";
	for(int i = 1; i <= n;i++){
		cout<

运行结果：

『例题一道』

---

【洛谷】P2872 [USACO07DEC]道路建设Building Roads   

原题链接：https://www.luogu.org/problemnew/show/P2872

Farmer John最近得到了一些新的农场，他想新修一些道路使得他的所有农场可以经过原有的或是新修的道路互达（也就是说，从任一个农场都可以经过一些首尾相连道路到达剩下的所有农场）。有些农场之间原本就有道路相连。 所有N(1 <= N <= 1,000)个农场（用1..N顺次编号）在地图上都表示为坐标为(X_i, Y_i)的点(0 <= X_i <= 1,000,000；0 <= Y_i <= 1,000,000)，两个农场间道路的长度自然就是代表它们的点之间的距离。现在Farmer John也告诉了你农场间原有的M(1 <= M <= 1,000)条路分别连接了哪两个农场，他希望你计算一下，为了使得所有农场连通，他所需建造道路的最小总长是多少。

输入输出格式

输入格式：

• 第1行: 2个用空格隔开的整数：N 和 M

• 第2..N+1行: 第i+1行为2个用空格隔开的整数：X_i、Y_i

• 第N+2..N+M+2行: 每行用2个以空格隔开的整数i、j描述了一条已有的道路， 这条道路连接了农场i和农场j

输出格式：

输出使所有农场连通所需建设道路的最小总长，保留2位小数，不必做 任何额外的取整操作。为了避免精度误差，计算农场间距离及答案时 请使用64位实型变量

输入输出样例

输入样例#1：

4 1
1 1
3 1
2 3
4 3
1 4

输出样例#1：

4.00

解题思路：

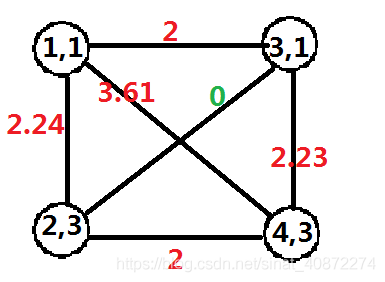
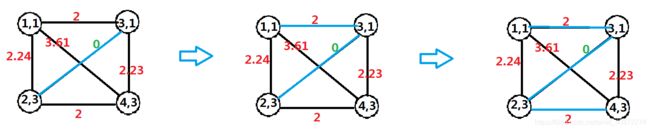
    将所有的顶点连接起来，补成一个完全图，n个顶点有共n*(n-1)/2条边。将题目中已存在的边（本来就有的路）的权值赋为0， 然后使用Kruskal算法生成最小生成树。

图示：

a.将所有顶点补成完全图

 b.将已经存在的边（原本就有的路）权值赋为0

c.进行Kruskal算法

  

下面直接上代码：

---

/*
解题思路：
    将原图补连成一个完全图，n个顶点有共n*(n-1)/2条边 将本存在的边的权值赋为0  然后Kruskal算法

************************
*/
#include 
#include 
#include 
#include 
#include 
using namespace std;
int f[1010];
struct Node {//点结构体
	int x,y;
} node;
struct Eage {//边结构体
	int v,u;
	double w;
} e;
vector vex;
vector eage;
bool cmp(const Eage&a,const Eage&b){//排序函数
	return a.w < b.w;
}
void Init() {//初始化
	for(int i = 1; i <= 1005; i++)
		f[i] = i;
}
double Getdis(double x1,double y1,double x2,double y2) {//计算距离函数
	double x = abs(x2-x1);
	double y = abs(y2-y1);
	return sqrt(x*x+y*y);
}
int check(int a){//查找到a的"根" 并返回 
	if(f[a] == a)
		return a;
	else{
		f[a] = check(f[a]);
	}
	return f[a];
}
bool merger(int a,int b){//将a和b归并到同一"根"下 
	int t1 = check(a),t2 = check(b);
	if(t1 == t2){
		return false;
	}else{
		f[t2] = f[t1];
		return true; 
	}
}
int main() {
	//输入数据
	double n,m,sum = 0;
	cin>>n>>m;
	Init();
	for(int i = 1; i <= n; i++) {
		cin>>node.x>>node.y;
		vex.push_back(node);
	}
	int a,b;
	for(int i = 1; i <= n; i++) {
		for(int j = i+1; j <= n; j++) {
			e.v = i;
			e.u = j;
			e.w = Getdis(vex[i-1].x,vex[i-1].y,vex[j-1].x,vex[j-1].y);
			eage.push_back(e);
		}
	}
	for(int i =1; i <= m; i++) {//这个地方原本打算将本身就存在边的权值改为0,后来发现过于繁琐.                  
                                //直接将赋值为0的新边加到vector后,在判断是否成环的时候,直接就                        
                                //会跳过旧的边
		cin>>a>>b;
		e.v = a;e.u = b;e.w = 0;	
		eage.push_back(e);
	}
	int len = eage.size();
	sort(eage.begin(),eage.end(),cmp);//排序
	int tot = 0;
	for(int i = 0; i < len; i++){
		if(merger(eage[i].v,eage[i].u))//如果不成环，加入到生成树中
		{
			sum = sum+eage[i].w;
			tot++;
			if(tot == n-1){
				printf("%.2f",sum);//注意格式
				break;
			}
		} 
	}
	return 0;
}