PCA和SVD

PCA的实现一般有两种，一种是用特征值分解去实现的，一种是用奇异值分解去实现的。

奇异值分解是一个有着很明显的物理意义的一种方法，它可以将一个比较复杂的矩阵用更小更简单的几个子矩阵的相乘来表示，这些小矩阵描述的是矩阵的重要的特性。

---

特征值基础知识：

特征值分解和奇异值分解的目的都是一样，就是提取出一个矩阵最重要的特征。

先谈谈特征值分解吧：
1）特征值：
如果说一个向量$v$是方阵$A$的特征向量，那么一定可以被表示成下面的形式：
$$Av=\lambda v$$
$\lambda$ 就称为特征值， $v$ 是特征值所对应的特征向量，一个矩阵的一组特征向量是一组正交向量。特征值分解是将一个矩阵分解成下面的形式：
$$A=Q\sum Q^{-1}$$
其中 $Q$ 是特征向量组成的矩阵，$\sum$ 是一个对角阵，每一个对角线上的元素就是一个特征值。要明确一点的是，一个矩阵其实就是一个线性变换，因为一个矩阵乘以一个向量后所得到的向量，其实就相当于将这个向量进行了线性变换。
比如说下面的一个矩阵：
$$M=\left[\begin{array}{cc}3& 0\\ 0& 1\end{array}\right]$$
它其实对应的线性变换是下面的形式：

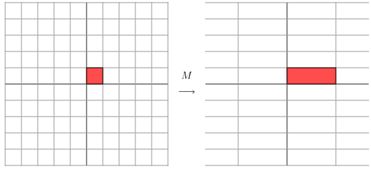
因为这个矩阵M乘以一个向量 $(x,y)$ 的结果是：
$$\left[\begin{array}{cc}3& 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}3x\\ y\end{array}\right]$$
这个变换是一个对$x$，$y$轴方向的拉伸变换（M矩阵中的第一列${\left[\begin{array}{cc}3& 0\end{array}\right]}^T$相当于拉长了基向量$i$，而基向量$j$不变）。
当矩阵是下面的样子：
$$M=\left[\begin{array}{cc}1& 1\\ 0& 1\end{array}\right]$$
它所描述的变换是下面的样子：

这其实是在平面上对一个轴进行拉伸变换（如蓝色的箭头所示）。在图中，蓝色的箭头是一个最主要的变化方向（变化方向可能有不止一个）。如果我们想要描述好一个变换，那我们就描述好这个变换主要的变化方向就好了。反过头来看看之前特征值分解的式子，分解得到的 $\sum$ 矩阵是一个对角阵，里面的特征值是由大到小排列的，这些特征值所对应的特征向量就是描述这个矩阵变化方向（从主要的变化到次要的变化排列）

当矩阵是高维的情况下，那么这个矩阵就是高维空间下的一个线性变换，这个线性变化可能没法通过图片来表示，但是可以想象，这个变换也同样有很多的变换方向，我们通过特征值分解得到的前$N$个特征向量，那么就对应了这个矩阵最主要的$N$个变化方向。我们利用这前$N$个变化方向，就可以近似这个矩阵（变换）。也就是之前说的：提取这个矩阵最重要的特征。
总结一下：
特征值分解可以得到特征值与特征向量，特征值表示的是这个特征到底有多重要，而特征向量表示这个特征是什么，可以将每一个特征向量理解为一个线性的子空间，我们可以利用这些线性的子空间干很多的事情。不过，特征值分解也有很多的局限，比如说变换的矩阵必须是方阵。

---

奇异值分解：

下面谈谈奇异值分解。特征值分解是一个提取矩阵特征很不错的方法，但是它只是对方阵而言的，在现实的世界中，我们看到的大部分矩阵都不是方阵，比如说有M个学生，每个学生有N科成绩，这样形成的一个M * N的矩阵就不可能是方阵，我们怎样才能描述这样普通矩阵的重要特征呢？奇异值分解可以用来干这个事情，奇异值分解是一个能适用于任意的矩阵的一种分解的方法：
$$A=U\sum V^T$$
假设$A$是一个$M\ast N$的矩阵，那么得到的$U$是一个$M\ast M$的方阵，$\sum$是一个$M\ast N$的矩阵（除了对角线的元素，其它都是$0$，对角线上的元素称为奇异值），$V^T$($V$的转置)是一个$N\ast N$的矩阵。
SVD分解如下图所示：

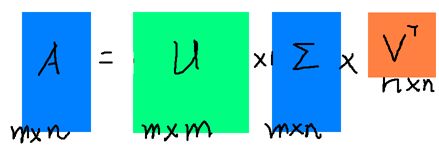
那么如何求出 $U,\Sigma ,V$ 这三个矩阵呢？
如果我们将 $A^T$ 和 $A$ 做矩阵乘法，那么会得到 $N\ast N$ 的一个方阵$A^{T}A$。既然 $A^{T}A$ 是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式
$$(A^{T}A)v_i={\lambda }_i{v}_i$$
这样就可以得到矩阵 $A^{T}A$ 的$N$个特征值和对应的$N$个特征向量 $v$ 了。将 $A^{T}A$ 的所有特征向量张成一个 $N\ast N$ 的矩阵 $V$，就是我们SVD公式里面的 $V$ 矩阵了。一般将 $V$ 中的每个特征向量叫做$A$的右奇异向量。

反之，

如果我们将 $A$ 和 $A^T$ 做矩阵乘法，那么会得到 $M\ast M$ 的一个方阵$A{A}^T$。既然 $A{A}^T$ 是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式：
$$(A{A}^T)u_i={\lambda }_i{v}_i$$
这样就可以得到矩阵 $A{A}^T$ 的 $M$ 个特征值和对应的 $M$个特征向量 $u$ 了。将 $A{A}^T$ 的所有特征向量张成一个 $M\ast M$ 的矩阵 $U$，就是我们SVD公式里面的 $U$ 矩阵了。一般将 $U$ 中的每个特征向量叫做 $A$ 的左奇异向量。

由于 $\sum$ 除了对角线上是奇异值，其他位置都是0，那我们只需要求出每个奇异值 $\sigma$ 即可。推导如下：
$$\begin{gathered} A=U\sum V^T \\ 在等式两边同时右乘V矩阵，得 \\ AV=U\sum V^{T}V \\ 由于V是方阵，根据方阵性质:V^{T}V=I,V^{T}V=V^2(V替换为U,\sum 同样适用) \\ AV=U\sum \\ A{v}_i={\sigma }_i{u}_i \\ {\sigma }_i=\frac{A{v}_i}{u_i} \end{gathered}$$

对于奇异值 $\sigma$ 的另外一种推导：
$$\begin{gathered} A=U\sum V \\ (A^{T}A)=(U\sum V{)}^T(U\sum V)=V^T\sum {}^T{U}^{T}U\sum V=V^T\sum {}^{2}V \end{gathered}$$
根据方阵的矩阵分解式：$X=Q\sum Q^{-1}$，对比即可发现，$A^T$ 与 $A$ 相乘，其特征值等于奇异值矩阵的平方。即：
$${\sigma }_i={\sqrt{\lambda }}_i$$
这样也就是说，我们可以不用 ${\sigma }_i=\frac{A{v}_i}{u_i}$ 来计算奇异值，也可以通过求出 $A^{T}A$ 的特征值取平方根来求奇异值。

---

SVD与PCA的关联

实现PCA主要依赖的两个原则是：
1.降维后的各个维度之间相互独立，即去除降维之前样本 $A$ 中各个维度之间的相关性。
2.最大程度保持降维后的每个维度数据的多样性，即最大化每个维度内的方差。

设矩阵$A$为$m\ast n$的样本矩阵，矩阵的每一行表示一个样本，每一列表示一个特征（也就是维度）。PCA的操作步骤为：
（1）求$A$均值
（2）将$A$减去均值
（3）计算协方差矩阵$C=\frac{1}{m}{A}^{T}A$ (除以m-1是无偏估计)
（4）对协方差矩阵$C$特征值分解
（5）从大到小排列$C$的特征值
（6）取前$k$个特征值所对应的特征向量，按列组成矩阵$P_{n\ast k}$（也称之为变换矩阵或投影矩阵）
（7）$A_{m\ast n}{P}_{n\ast k}$

核心问题就是协方差矩阵 $C=\frac{1}{m}{A}^{T}A$的特征值分解

为什么对协方差矩阵求解特征值不是最好的方法呢？原因有以下几点：
1.如果$A$的维度很高，则$A^{T}A$的计算量很大
2.方阵的特征值分解计算效率不高
3.如果矩阵A中的数很小，例如有自然对数$e$，则求解协方差时，会损失数据精度

那为什么会用到SVD呢？
$$\begin{gathered} 令X=\frac{A}{\sqrt{m}} \\ {X}^{T}X=(\frac{A}{\sqrt{m}}{)}^T\frac{A}{\sqrt{m}} \\ {X}^{T}X=\frac{1}{m}{A}^{T}A \end{gathered}$$
观察上述推导
第一：$X=\frac{A}{\sqrt{m}}$ 此时，X是一个矩阵，可以进行SVD奇异值分解。
第二：右奇异向量$V$的推导，是通过$X^{T}X$特征值分解得出的。【矩阵X奇异值分解，自然是用$X^{T}X$】
第三：$X^{T}X=\frac{1}{m}{A}^{T}A$，此时左右两边矩阵等价，也就是说，$X^{T}X$此时求解的特征值和特征向量，即为协方差矩阵所要求的特征值和特征向量。而这个特征向量所张成的矩阵就是右奇异向量V。

【补充】 为什么这儿还是用的特征值分解矩阵，前面不是说矩阵维度高，或矩阵元素的数值很小时会损失精度吗？
我从网上所查阅到的解释是：SVD除了特征值分解这种求解方式外，还有更高效且更准确的迭代求解法，避免了$X^{T}X$的计算。

【补充】当使用某个数据去验证上述推导时，协方差矩阵的计算可以使用Matlab的cov函数。自己去计算$X^{T}X$时，要先将$X$去均值（中心化），得到的结果才一致。因为matlab里面的函数默认对列进行去均值。

---

SVD应用

在对角矩阵$\sum$中，奇异值$\sigma$是按照从大到小的顺序排列，而且$\sigma$的减小特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说，我们也可以用前$r$大的奇异值来近似描述矩阵。
这里定义一下部分奇异值分解：
$$A_{m\ast n}\approx U_{m\ast r}\begin{array}{c}{\sum }_{r\ast r}\end{array}{V}_{r\ast n}^T$$
$r$是一个远小于$m、n$的数，这样矩阵的乘法看起来是下面的样子：

右边的三个矩阵相乘的结果将会是一个接近于$A$的矩阵，在这儿，$r$越接近于$n$，则相乘的结果越接近于$A$。而这三个矩阵的面积之和（在存储观点来说，矩阵面积越小，存储量就越小）要远远小于原始的矩阵A。我们如果想要压缩空间来表示原矩阵A，我们存下这里的三个矩阵：U、Σ、V就好了。

压缩（降维）

设矩阵 $A$ 为 $m\ast n$ 的样本矩阵，矩阵的每一行表示一个样本($m$是样本个数)，每一列表示一个特征（也就是维度，$n$维）。

降维的目的是将一个 $m\ast n$ 的矩阵 $A$ 变换成一个 $m\ast r$ 的矩阵，这样就会使得本来有 $n$ 个维度变成 $r$ 个维度了（r < n)。这 $r$ 个维度其实就是对 $n$ 个维度的一种压缩，也称之为降维。用数学语言表示就是：
$$A_{m\ast n}{P}_{n\ast r}=A_{m\ast r}式①$$
但是这个式子怎么和SVD扯上关系呢？首先看奇异值分解的式子：
$$A_{m\ast n}\approx U_{m\ast r}\begin{array}{c}{\sum }_{r\ast r}\end{array}{V}_{r\ast n}^T$$
在矩阵的两边同时乘上一个矩阵 $V$，由于 $V$ 是一个正交的矩阵，所以 $V^{T}V=I$，从而有:
$$\begin{gathered} A_{m\ast n}{V}_{n\ast r}\approx U_{m\ast r}\begin{array}{c}{\sum }_{r\ast r}\end{array}{V}_{r\ast n}^T{V}_{n\ast r} \\ {A}_{m\ast n}{V}_{n\ast r}\approx U_{m\ast r}\begin{array}{c}{\sum }_{r\ast r}\end{array}式② \end{gathered}$$

将式①与式②对比，在这里，其实$V$就是$P$，也就是一个变化的向量。这里是将一个 $m\ast n$ 的矩阵压缩到一个 $m\ast r$ 的矩阵，也就是对列进行压缩。

【注意：$U$和$V$矩阵都是特征向量按照列所张成的矩阵。在上面的式子上，$V_{r\ast n}^T$中的下标$r\ast n$表示的是$V_{n\ast r}$矩阵转置以后的矩阵尺寸，即为$r\ast n$】

如果我们想对行进行压缩（在PCA的观点下，对行进行压缩可以理解为，将一些相似的sample合并在一起，或者将一些没有太大价值的sample去掉）怎么办呢？同样我们写出一个通用的行压缩例子：
$$P_{r\ast m}{A}_{m\ast n}=A_{r\ast n}$$
这样就从一个$m$行的矩阵压缩到一个$r$行的矩阵了，对SVD来说也是一样的，我们对SVD分解的式子两边乘以$U$的转置$U^T$
$$U_{r\ast m}^T{A}_{m\ast n}\approx \begin{array}{c}{\sum }_{r\ast r}\end{array}{V}_{r\ast n}^T$$
这样我们就得到了对行进行压缩的式子。可以看出，其实PCA几乎可以说是对SVD的一个包装，如果我们实现了SVD，那也就实现了PCA了。而且更好的地方是，有了SVD，我们就可以得到两个方向的PCA，如果我们对$A^{T}A$进行特征值的分解，只能得到一个方向的PCA。

【补充】
PCA用来降维时：n维 ——> k维 （k PCA用来去噪时：n维 ——> k维 ——> n维 （先降维，在重构）

---

Matlab带有pca和svd函数。遇到的困惑是：对同一个数据，分别通过pca操作和svd操作以后，发现数据结果不一致。

[u,s,v]=svd(A)

需要对数据A去均值（中心化），在令$X=\frac{A}{\sqrt{m-1}}$，在用X替换A即可。

实际上$X$除以$\sqrt{m-1}$只是相当于缩放（Scaling），改变的是波形振幅，并不真正的影响波形变换趋势。