自然语言处理——语言模型(一)

引言

本文简单介绍了一下语言模型和马尔科夫假设。

语言模型简介

语言模型(Language Model,LM)是计算给定句子或单词序列$w$出现概率$p(w)$的模型，用来判断一句话是否通顺。

这里说的单词不只是代表英语单词，还代表中文词语。

比如“今天是周日”和“今天周日是”这两句话，前者显然比后者更加通顺。在机器翻译领域，语言模型可以把后者修正为前者这种通畅的表达。

那语言模型是如何判断哪个句子更好的呢，是通过概率的方式。

比如我们的语言模型能得到 P(“今天是周日”) > P(“今天周日是”)。

那如何计算一个句子的概率呢，假设句子$w$由$w_1,w_2,\cdots ,w_n$这些单词组成。
那么$p(w)=p(w_1,w_2,\cdots ,w_n)$。

下面就来说明如何计算一个句子或单词序列出现的概率，首先介绍一下马尔科夫假设。

马尔科夫假设

在介绍马尔科夫假设(Markov assumption)之前要介绍一下概率论的链式法则。

假设有两个随机变量$A,B$，如何把$P(A,B)$表示成条件概率呢。
由概率论知识可知：
$$P(A,B)=P(A|B)\cdot P(B)=P(B|A)\cdot P(A)$$

那如果有四个随机变量$A,B,C,D$呢，如何求$P(A,B,C,D)$，也是一样的。
$$\begin{array}{rl}P(A,B,C,D)& =\underline{P(A)\cdot P(B|A)}\cdot P(C|A,B)\cdot P(D|A,B,C)\\ & =\underline{P(A,B)}\cdot P(C|A,B)\cdot P(D|A,B,C)\\ & =P(A,B,C)\cdot P(D|A,B,C)\\ & =P(A,B,C,D)\end{array}$$

注意我们多次利用了$P(A,B)=P(B|A)\cdot P(A)$的形式。

$P(A,B,C,D)=P(A)\cdot P(B|A)\cdot P(C|A,B)\cdot P(D|A,B,C)$这个就叫概率论的链式法则。

我们知道，计算事件$B$发生的条件下事件$A$发生的条件概率为：
$$P(A|B)=\frac{P(A,B)}{P(B)}$$
把分母乘到左边就得到了链式法则。

那么我们把句子中的每个单词看成是随机变量的话，就可以通过链式法则来求句子$p(w)$的概率：
$$\begin{array}{rl}p(w)& =p(w_1,w_2,\cdots ,w_n)\\ & =p(w_1)\cdot p(w_2|w_1)\cdot P(w_3|w_1{w}_2)\cdots p(w_n|w_1{w}_2\cdots w_{n-1})\end{array}$$

下面我们来看下通过链式法则如何表达句子“今天\是\春节\我们\都\休息”的联合概率。

$p(今天,是,春节,我们,都,休息)=p(今天)\cdot p(是|今天)\cdot p(春节|今天,是)\cdot p(我们|今天,是,春节)\cdot p(都|今天,是,春节,我们)\cdot p(休息|今天,是,春节,我们,都)$

只要我们有一个很大的语料库，我们就可以提前计算好上面的这些概率，比如计算$p(今天)$只需要计算单词“今天”出现的次数除以单词总数；计算$p(是|今天)$就是计算单词“今天”后面接单词“是”的次数除以单词“今天”出现的次数。

因为语言是创造性的，你可能会碰到“一给我里giaogiao，你有没有搞错。”，这种序列可能你的训练集中根本就没有(最近流行的网络词+随意组合)，导致这个序列的概率是零。

为了解决这个问题，我们引入了马尔科夫假设，也就是假设当前词出现的概率只依赖于前$n-1$个词，比如，$n=2$，就是当前单词只依赖于前一个词，
那么$p(休息|今天,是,春节,我们,都)\approx p(休息|都)$

如果$n=3$，那么意味着当前单词依赖于前两个单词，
即$p(休息|今天,是,春节,我们,都)\approx p(休息|我们,都)$

更一般地，如果求$p(w_1,w_2,w_3,w_4,w_5,\cdots ,w_n)$。

• 当$n=2$时,
  $$\begin{gathered} p(w_1,w_2,w_3,w_4,w_5,\cdots ,w_n)=p(w_1)\cdot p(w_2|w_1)\cdot p(w_3|w_2)\cdots p(w_n|w_{n-1}) \\ =p(w_1)\prod _{i=2}^{n}p(w_i|w_{i-1}) \end{gathered}$$
• 当$n=3$时,
  $$\begin{gathered} p(w_1,w_2,w_3,w_4,w_5,\cdots ,w_n)=p(w_1)\cdot p(w_2|w_1)\cdot p(w_3|w_1,w_2)\cdot p(w_4|w_2,w_3)\cdots p(w_n|w_{n-2},w_{n-1}) \\ =p(w_1)\cdot p(w_2|w_1)\prod _{i=3}^{n}p(w_i|w_{i-2},w_{i-1}) \end{gathered}$$

下面来看一个实例，让我们更好地理解这里面的思想。

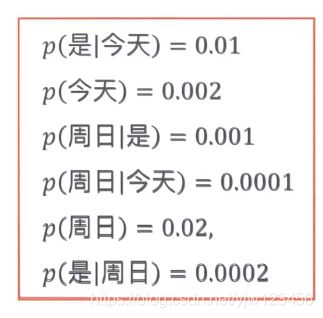
假设我们已经从语料库中得到上面的概率。
下面我们令$n=2$，只依赖前一个单词的形式来比较句子“今天\是\周日”和“今天\周日\是”的概率。

$$\begin{array}{rl}p(今天是周日)& =p(今天)\cdot p(是|今天)\cdot p(周日|是)\\ & =0.002\times 0.01\times 0.001\\ & =2\times 10^{-8}\end{array}$$

再来看另一个句子
$$\begin{array}{rl}p(今天周日是)& =p(今天)\cdot p(周日|今天)\cdot p(是|周日)\\ & =0.002\times 0.0001\times 0.0002\\ & =4\times 10^{-10}\end{array}$$

也就是“今天是周日”出现的概率要大一些，我们就认为它是二者之间语义最优的。

下篇文章将会介绍N-Gram语言模型。

参考

1. 贪心学院课程