Codeforces Round #618 (Div. 2)D,E
D. Aerodynamic
time limit per test1 second
memory limit per test256 megabytes
inputstandard input
outputstandard output
Problem Description
Guy-Manuel and Thomas are going to build a polygon spaceship.
You’re given a strictly convex (i. e. no three points are collinear) polygon P which is defined by coordinates of its vertices. Define P(x,y) as a polygon obtained by translating P by vector (x,y)−→−−. The picture below depicts an example of the translation:
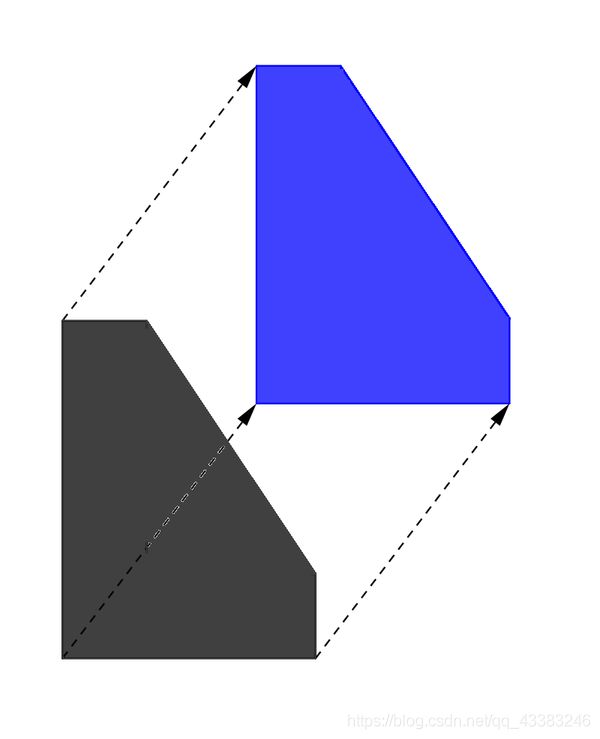
Define T as a set of points which is the union of all P(x,y) such that the origin (0,0) lies in P(x,y) (both strictly inside and on the boundary). There is also an equivalent definition: a point (x,y) lies in T only if there are two points A,B in P such that AB−→−=(x,y)−→−−. One can prove T is a polygon too. For example, if P is a regular triangle then T is a regular hexagon. At the picture below P is drawn in black and some P(x,y) which contain the origin are drawn in colored:
The spaceship has the best aerodynamic performance if P and T are similar. Your task is to check whether the polygons P and T are similar.
Input
The first line of input will contain a single integer n (3≤n≤105) — the number of points.
The i-th of the next n lines contains two integers xi,yi (|xi|,|yi|≤109), denoting the coordinates of the i-th vertex.
It is guaranteed that these points are listed in counterclockwise order and these points form a strictly convex polygon.
Output
Output “YES” in a separate line, if P and T are similar. Otherwise, output “NO” in a separate line. You can print each letter in any case (upper or lower).
Examples
input
4
1 0
4 1
3 4
0 3
output
YES
input
3
100 86
50 0
150 0
output
nO
input
8
0 0
1 0
2 1
3 3
4 6
3 6
2 5
1 3
output
YES
Note
The following image shows the first sample: both P and T are squares. The second sample was shown in the statements.

【题意】
给定一个图形(凸多边形),平移这个图形,使得原点在这个图形内(包括边和点),求这两个图形是否相似。
求这个图形是否中心对称,其实看到原点这个条件就应该这么想。
#include
using namespace std;
typedef long long ll;
const int maxn=1e5+10;
ll a[maxn],b[maxn];
int main()
{
ios::sync_with_stdio(false);
ll n;
cin>>n;
for(int i=1;i<=n;i++)
cin>>a[i]>>b[i];
if(n%2==1)
{
cout<<"NO"< E
E. Water Balance
time limit per test
3 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output
There are nn water tanks in a row, ii-th of them contains aiai liters of water. The tanks are numbered from 11 to nn from left to right.
You can perform the following operation: choose some subsegment [l,r][l,r] (1≤l≤r≤n1≤l≤r≤n), and redistribute water in tanks l,l+1,…,rl,l+1,…,r evenly. In other words, replace each of al,al+1,…,aral,al+1,…,ar by al+al+1+⋯+arr−l+1al+al+1+⋯+arr−l+1. For example, if for volumes [1,3,6,7][1,3,6,7] you choose l=2,r=3l=2,r=3, new volumes of water will be [1,4.5,4.5,7][1,4.5,4.5,7]. You can perform this operation any number of times.
What is the lexicographically smallest sequence of volumes of water that you can achieve?
As a reminder:
A sequence aa is lexicographically smaller than a sequence bb of the same length if and only if the following holds: in the first (leftmost) position where aa and bb differ, the sequence aa has a smaller element than the corresponding element in bb.
Input
The first line contains an integer nn (1≤n≤1061≤n≤106) — the number of water tanks.
The second line contains nn integers a1,a2,…,ana1,a2,…,an (1≤ai≤1061≤ai≤106) — initial volumes of water in the water tanks, in liters.
Because of large input, reading input as doubles is not recommended.
Output
Print the lexicographically smallest sequence you can get. In the ii-th line print the final volume of water in the ii-th tank.
Your answer is considered correct if the absolute or relative error of each aiai does not exceed 10−910−9.
Formally, let your answer be a1,a2,…,ana1,a2,…,an, and the jury's answer be b1,b2,…,bnb1,b2,…,bn. Your answer is accepted if and only if |ai−bi|max(1,|bi|)≤10−9|ai−bi|max(1,|bi|)≤10−9 for each ii.
Examples
input
Copy
4
7 5 5 7
output
Copy
5.666666667
5.666666667
5.666666667
7.000000000
input
Copy
5
7 8 8 10 12
output
Copy
7.000000000
8.000000000
8.000000000
10.000000000
12.000000000
input
Copy
10
3 9 5 5 1 7 5 3 8 7
output
Copy
3.000000000
5.000000000
5.000000000
5.000000000
5.000000000
5.000000000
5.000000000
5.000000000
7.500000000
7.500000000
Note
In the first sample, you can get the sequence by applying the operation for subsegment [1,3][1,3].
In the second sample, you can't get any lexicographically smaller sequence.
【题意】
给定一个序列,可以选择一个[l, r]区间,使得这个区间内的所有值替换为这个区间内的平均值。
可以对这个序列操作任意次,使得这个序列字典序最小,问这个最小字典序的序列是什么。
【思路】
假设已经有两个区间[l1, r1],[l2, r2],区间内的值分别为x1,x2,当前有一个数k加入这两个区间之后,可以知道,如果k 用cin,cout还会超时,,cf做到后面的话直接就scanf吧,避免不必要的wa。#include