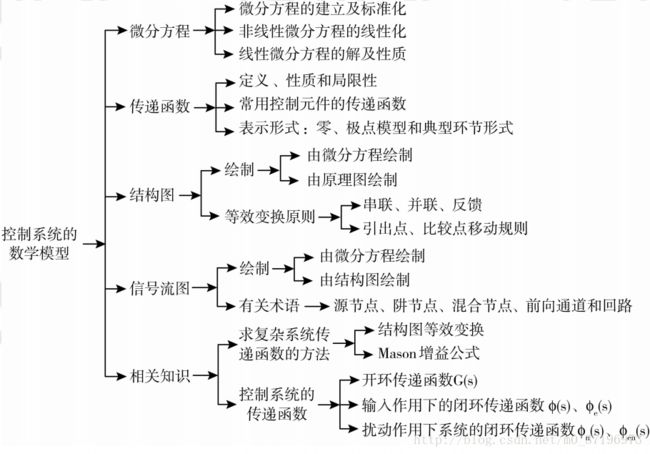
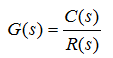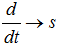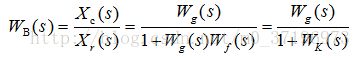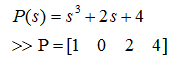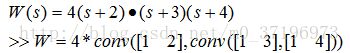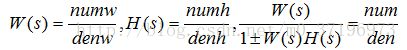自动控制原理02 数学模型
在经典控制理论当中有三个理论基石:时域分析法,根轨迹法、频域分析法。
这三种方法只是我们分析系统的一种手段,不管采用哪种方法,都离不开系统的数学模型。
一 微分方程
在时域当中的数学模型,叫做微分方程。
我们首先列出原始平衡方程,对这些原始平衡方程进行化解得到标准形式,并且利用微分方程的求解得到微分方程的解,从这些解当中,我们分析控制系统的性能。
二 传递函数
(1) 零、极点的模型形式, 在根轨迹法中常见到 ;在复频域当中的数学模型,叫做传递函数。
传递函数有两种重要的表现形式:
(2)典型环节的形式,如传递函数等于由一些比例环节或者是一阶的微分环节或者是二阶的微分环节比上积分环节或者一阶惯性环节或者二阶的震荡环节等等,在频域分析法中常见到。
(1)传递函数针对的是 线性的定常系统 , 非线性系统或者变系数系统都不能使用传递函数来表述它的数学模型 ;传递函数定义的前提条件是:
(2) 要在 零初始条件 下。 零初始条件 是指:在时间t=0时刻,输出的各阶导数都等于0,并且t=0时刻,系统没有输入。
满足两个前提条件的情况下,输出的拉氏变换与输入的拉氏变换的比值,定义为系统的传递函数。
将微分方程中的微分算子换成复频域中的变量s,即:
则可将微分方程转换为系统传递函数。
传递函数这样的数学模型有着它自身的性质,这些性质对于分析系统而言非常重要。主要包括以下几种:
1. 由于能量传递总是有限,所以微分方程输出端的阶次总是会高于输入端的阶次,其对应的传递函数分子多项式的阶次就小于或等于分母多项式的最高阶次,并且传递函数描述的是一个线性定常的系统,故其对应的所有系数都是实数 ;
2. 传递函数是系统的一种固有属性,与外加激励及初始条件无关(这在传递函数的定义中可以了解到,传递函数是在零初始条件下定义的);
3. 传递函数只是对系统的数学描述,并不反应系统的物理构成。
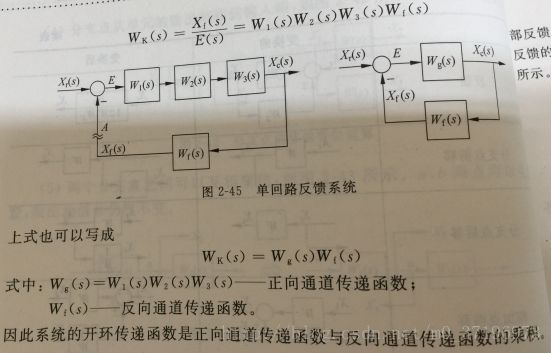
系统开环传递函数
如图,从A点断开由E(s)到Xf(s)之间各串联环节传递函数的乘积,就是系统的开环传函。
系统闭环传递函数
对上图中的系统,闭环传递函数为:
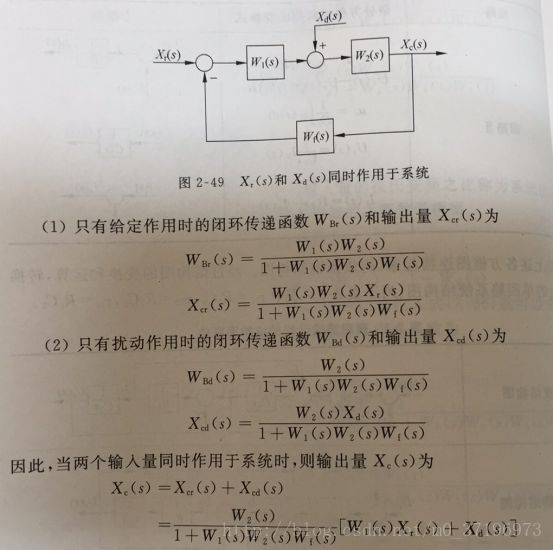
系统对给定作用和扰动作用的传递函数
对线性系统来说,可对每一个输入量分别求出输出量,然后进行叠加,得到系统的输出量。
三 动态结构图
我们从抽象的物理系统中分析它的工作原理,建立它的动态结构图。动态结构图绘制出来之后,我们还需对其进行等效,得到系统最终的传递函数,从而分析它的性能。
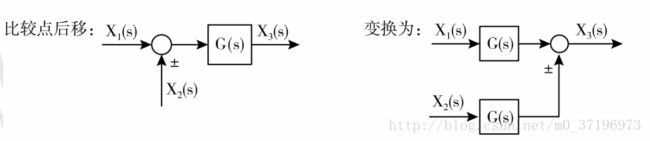
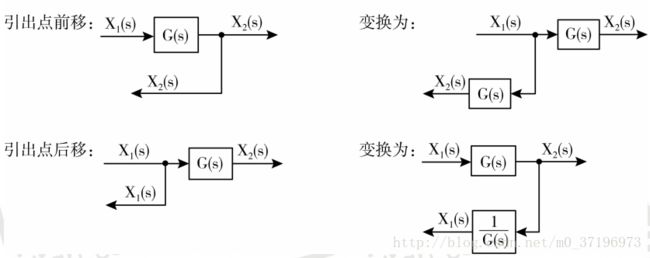
在动态结构图中的等效当中,我们会经常见到这样的几种等效原则: 串联、并联、反馈以及引出点和比较点的移动。
1. 比较点前移、后移
2. 引用点前移、后移
四 信号流图
信号流图的绘制有两种方式:
(1)从时域微分方程或者代数方程中绘制;
(2)从动态结构图中绘制。
信号流图的绘制并不重要,因为我们只要知道了动态结构图,再利用Mason增益公式,对于任何系统,它的传递函数都可以很容易获得。
举例说明梅森公式的使用
用MATLAB求解线性微分方程和化简系统方框图
MATLAB中多项式用行向量表示,系数降幂排列,如:
乘法处理函数调用格式为C=conv(A,B),其调用允许多级嵌套,如:
系统传递函数可由其分子分母多项式唯一确定,格式为sys=tf(num,den). num为分子多项式,den为分母多项式。
多项式求根函数调用格式为roots(p),p为多项式系数向量。
若特征根已求出,可调用poly(r)函数求多项式降幂排列的各项系数,r为已求出的特征根
polyval()函数可用来求取给定变量值时多项式的值,其调用格式为polyval(p,a),p为多项式系数向量,a为给定变量值。
零极点模型的构造函数调用格式为
z=[z1;z2;...;zn];
p=[p1;p2;...;pn];
w=zpk(z,p,k)
z为系统零点列向量,p为极点列向量,k为系统增益。
求解线性微分方程
residue()函数用于部分分式展开,直接求出展开式中的留数、极点和整数项。调用格式为[r,p,k]=residue(num,den), r和p分别为各部分分式的留数与极点,k为整数项。图
方框图化简
W1(s)和W2(s)串联,串联函数series(), 调用格式为[num,den]=series(num1,den1,num2,den2),其中
并联函数parallel(), 调用格式为[num,den]=parallel(num1,den1,num2,den2),其中
反馈函数feedback(),调用格式为[num,den]=feedback(numw,denw,numh,denh,sign),其中W(s)为正向通道传函,H(s)为反向通道传函,sign为反馈极性,“1”为正反馈,“-1”为负反馈(不指明则默认为负)
图
参考,仅作个人学习笔记使用。