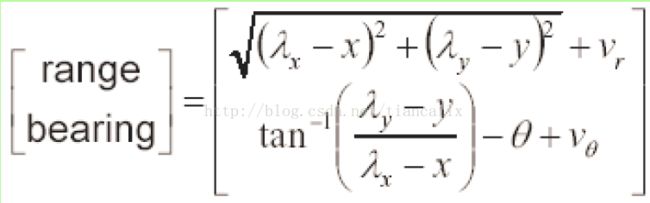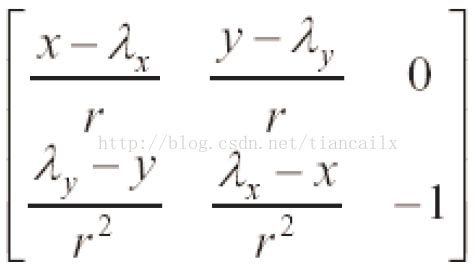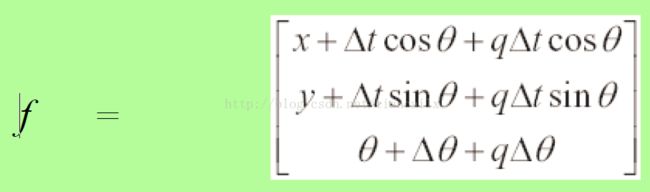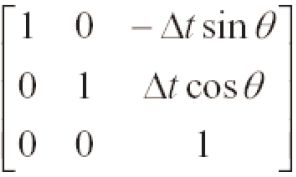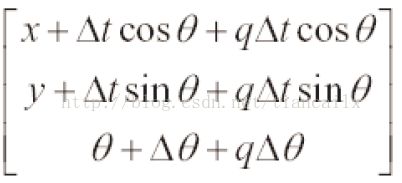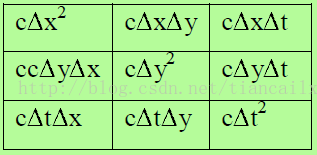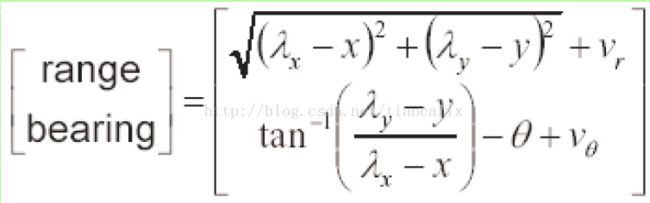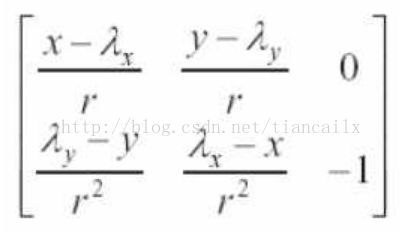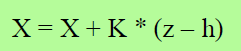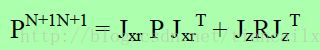EKF_SLAM一般过程
SLAM，同步定位与地图构建，本文将介绍基于EKF的SLAM的整体过程。
1 EKF_SLAM Overview
当机器人处在个未知环境中时，他最想知道的就是他在当前环境中的位置。环境不知道咋办，通过传感器获得，如里程计，激光雷达，摄像头等。机器人收到的数据是相当多的，但是并不是所有的数据都可以用来定位。首先需要在这些传感器信息中提取出地标，然后根据这些地标进行卡尔曼滤波的 预测 - 更新 过程。该过程得到的是地图与机器人位姿的联合概率密度。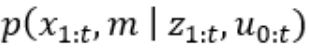
EKF是一种基于概率模型的状态和参数的估计方法，通常用于解决非线性系统模型的估计问题。EKF是对标准Kalman滤波进行扩展，用Taylor级数展开的一阶项来近似非线性的方程，从而运用 Kalman 滤波对系统状态进行递归估计【3】，以测量误差为依据进行估计和校正，不断逼近真实值（就是EKF对非线性系统线性化，之后再利用卡尔曼滤波进行线性系统的估计）。
2 地标提取与数据关联
从统计的角度讲SLAM问题是一个滤波问题。扩展Kalman滤波可以很好除去系统中的高斯噪声干扰，从里程计数据与地标观察值里估计出机器人的位置（状态估计）。
（以激光为例）当激光数据到达时，首先对该数据进行地标提取，之后通过数据关联判断该地标是否是以前观测到的，如果不是则将该地标加入状态更新过程。
2.1 地标提取（Landmark Extraction）
地标（Landmarks）用于机器人的定位，需要满足一下条件才可以称之为地标。
- 可以在不同位置不同角度重复被观察到（被观察次数大于N次）；
- 地标应该足够特殊以便可以从不同时间步中区分出是否是同一地标；
- 在环境中地标的数量应该很多；
- 地标必须静止。
2.2 数据关联（Data Association）
SLAM中的数据关联是指建立在不同时间、不同地点的传感器测量之间、传感器测量与地图特征之间或者地图特征之间的对应关系，以确定它们是否源于环境中同一物理实体的过程【4】。
数据关联时可能会出现如下状况：
- 可能某个地标不能在每个时间步中都被重复观察到
- 可能在以后都看不到该地标
- 可能错误的将某个地标当做以前观测到的某个地标
前两种情况可以通过地标提取算法轻易的避免掉，因为它不满足地标的条件。
最近邻方法（Nearest Neighbour, NN）
新息是模型输出预测值和实测值之差
该方法通过度量预测的观测值与实际的观测值的马氏距离（Mahalanobis Distance），也叫归一化平方新息(Normalised Innovation Squared，NIS)，与阈值lambda进行比较，来判断观测到的陆标与地图中已经存在的陆标之间的对应关系，即：
归一化平方新息是新息向量的加权范数，设由某一观测 z 和预测 zˆ 确定的新息为
,
v的方差为S.当满足如上条件时，则将两个地标视为同一个地标。
地标提取与数据关联之后，就是EKF的主要过程了。
- 预测：使用当前里程计来估计下一时刻机器人的位置估计
- 更新：根据重复观测到的地标更新状态估计
- 将新地标加入当前状态中
3 EKF数学模型（所需矩阵定义）
系统状态矩阵 X：
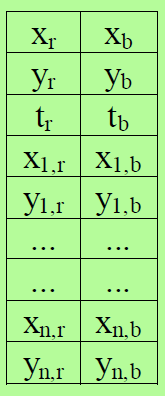
他包含了机器人的位姿，x y theta 以及地标的 x y 。
相关数学概念：
协方差（Covariance）在概率论和统计学中用于衡量两个变量的总体误差。两个变量的协方差提供了这两个变量相关程度的度量。相关性是用来衡量变量间线性相关程度的一个概念。
协方差矩阵可用来表示多维随机变量的概率密度，从而可通过协方差矩阵达到对多维随机变量的研究。
协方差矩阵 P : 
该矩阵记录了机器人位姿的协方差，地标的协方差，机器人与地标以及地标与地标之间的协方差。且当机器人连续观察地图中的特征点时，协方差矩阵任何子矩阵的行列式呈单调递减。从理论上讲，当观测次数趋向于无穷时，每个特征标志的协方差只与机器人起始位姿的协方差有关【3】。
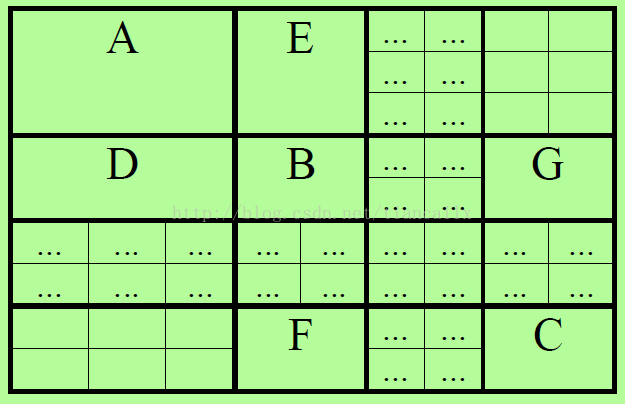
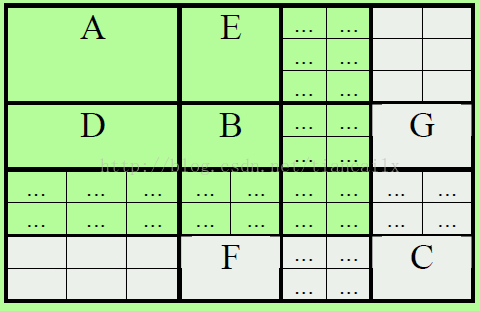
Ａ包含了机器人位姿的协方差，由于机器人位姿为x y theta ，所以该矩阵式3 * 3 的
P主对角线上的矩阵 B ，C 为地标位置的协方差。
D E 为机器人与地标之间的协方差。
F G 为地标之间的协方差，地标的变量只有两个，x y ， 所以该矩阵为2 * 2的。
卡尔曼增益 K : 
对收到的信息的置信程度，越相信，K越高，反之越低。
上述矩阵每一行代表每一个维度，也就是每个变量，两列分别为距离与方向的置信程度。
测量模型 h ；
测量模型定义如何计算观察到的地标相对于位置的预期距离和方位（根据机器人位置估计地标）。lambda x 为地标的x坐标，x为估计出的机器人当前位置。
测量模型的雅可比矩阵 H ：
雅可比矩阵表示的地标的位置与方位角随着机器人位置和方位角变化的程度。第一行的第一个元素为地标随着机器人x坐标变化时的距离变化值；第二个元素为相对于机器人y坐标变化时的距离变化值；最后一项为地标相对于机器人的角度的距离变化值。可以看出，当机器人做纯旋转运动时，地标相对于机器人的距离信息当然不会变化。第二行表示的地标所处角度相对于机器人坐标变化的情况。上面的雅可比矩阵式我们使用EKF时常见的雅可比矩阵。在做SLAM时，我们通常需要一些额外的信息，如下
其中第一行仅用作指示，并不是矩阵的一部分。上面意味着前三列为常规雅可比矩阵。对于每一个地标，我们增加两列，上图所示即为第二个地标的观测雅可比矩阵，其余地标的雅可比矩阵各元素为0。
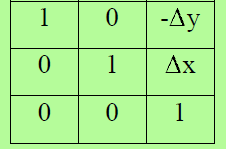
预测模型的雅可比矩阵：A
预测模型的雅可比矩阵可以通过预测模型计算出来，预测模型为：
然后不知道怎么就算出了预测模型的雅克比矩阵：
在做SLAM的时候，还有两个Jacobian与EKF过程不同，它只用在SLAM中的在新特征的整合时。这也是与使用EKF的常规状态估计不同的唯一步骤。
首先是Jxr。 除了我们从旋转项开始外，它和预测模型的雅可比基本相同。这是地标的预测的雅可比，其不包括theta的预测，相对于来自X的机器人状态[x，y，θ]：
Jacobian Jz也是地标的预测模型的雅可比，但这次是关于[range，bearing]的：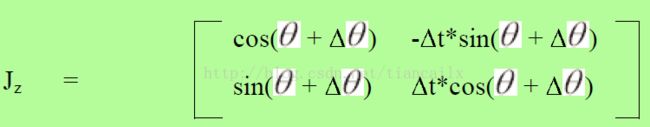
控制噪声 Q: 
这里，我们假设系统中的噪声为高斯噪声，且与控制量成正比。过程噪声的协方差矩阵为3*3的矩阵.
测量噪声 V & R :
R : 
, V 是一个2*2的单位矩阵
4 EKF过程
4.1 预测阶段
1 使用控制量进行下一时刻机器人位姿的估计
每一步都是根据前一时刻的位姿进行预测，那么初始时刻的位姿怎么确定呢？《SLAM for Dummies》中有这样一句话，里程计数据提供了机器人的近似位置，可以作为机器人在EKF中的初始位置猜测。
2 之后根据该估计出的位姿更新状态矢量X、预测模型的雅克比矩阵A、以及控制的噪声矩阵Q
A:
Q: 
3 对该机器人位姿进行协方差矩阵P的更新
首先计算机器人自身的协方差（P的左上方3*3的子矩阵）
（等式左边代表P的左上方3*3的子矩阵）
之后更新机器人与地标之间的协方差矩阵，
（也就是P的前三行或者前三列，P是对称阵）
4.2 更新阶段
由于机器人运动模型的误差，在第一步中我们得到的机器人位置并不是机器人真实的位置，因而，我们需要通过观测值对上述估计进行修正。使用机器人观测到的地标来计算机器人位置与估计值间的差异，进一步的，我们可以更新机器人位置的估计值。
这个步骤是针对每个重新观察到的地标（以前看到过的）进行的。新地标的合并会在第三步中进行。延迟新地标的合并可以使协方差矩阵P和系统状态X维度较小，从而减小计算复杂度。
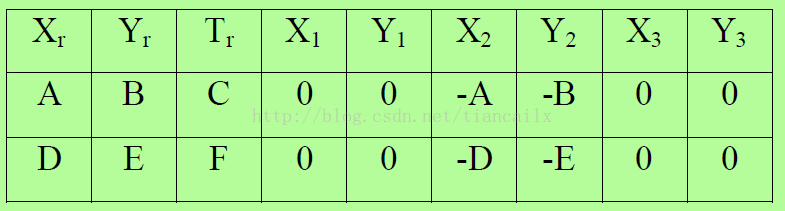
1 我们将根据当前机器人位置的估计值以及目前存储的地标位置利用下面的公式计算地标位置和角度的预测值：
之后根据
即可计算出测量模型的雅可比矩阵 H
注：只有前三列和当前地标有效的列应需要填写。
2 更新测量噪声R
3 计算卡尔曼增益
卡尔曼增益表示的是如何根据当前估计值与测量值更新当前的估计值
术语（H * P * HT + V * R * VT）被称为 新息协方差矩阵 S。
（观测的 新息 为根据当前机器人估计位姿，计算出的预测地标位置与下一时刻观测得到的地标位置的差异）
4 最后，我们可以使用上述卡尔曼增益计算一个新的状态向量
z为在 t 时刻 的 机器人位姿 X（t） 下观测到的地标距离与方向。
h为 t-1 时刻 根据机器人估计位姿 X~（t-1) 预测出的地标的位置。
等式右侧的 X 为根据里程计预测模型 估计出的机器人位姿
等式左侧的 X 为根据观测模型 更新后的机器人位姿，也更接近真实位姿。
上式将会更新当前机器人位置以及各个地标的位置。
上述步骤对每一个地标均重复进行，直至对所有地标完成计算。
4.3 添加新的地标
在这一步，我们要将新的地标加入到状态矢量X和协方差矩阵P中。
1 首先我们将新的标志添加到状态矢量X.
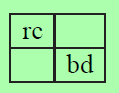
2 如下图所示，将一个新的地标 C 加入到协方差矩阵中
其中：
更新后的协方差矩阵有N+1个地标，记为
机器人位姿与地标位置的协方差记为
，另一个为该子矩阵的转置。
地标位置间的协方差矩阵为
，另一侧为该子矩阵的转置。
至此，完成了SLAM过程的最后一步。 机器人现在可以再次移动，观察地标，关联地标，使用测距法更新系统状态，使用重新观察的地标更新系统状态，最后添加新的地标。
-----------------------------------------------
REFERENCES：
【1】《SLAM for Dummies-A Tutorial Approach to Simultaneous Localization and Mapping》
大部分内容来自对该文章的翻译
【2】https://zhuanlan.zhihu.com/p/21381490 ： 有些参考于知乎上的这篇文章
【3】大尺度环境下移动机器人同时定位与地图创建研究_郭利进
【4】机器人同步定位与建图中数据关联问题研究_季秀才