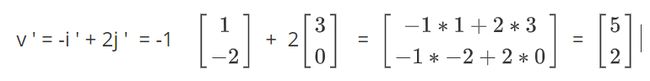零公式学线代！纯纯纯几何视角下的线性代数

观前提醒：文章前后关联性较强，后文都是在前文的几何概念上展开。建议顺序阅读

什么是向量？

三种视角看向量

物理专业视角：向量是有方向的箭头 eg: ----->

计算机专业视角：向量是有序的数字列表 eg:[1, 2]

数学专业视角： 向量是任何东西！只要能保证其两个相加或与常数相乘是有意义的。eg：小松鼠是向量，松鼠+松鼠 = 松鼠宝宝；3 * 松鼠 = 三只松鼠

tips：我们将不断加深数学专业的视角上的向量理解，由于本篇着重讲述几何本质，我们可以用物理和计算机专业的视角去想象向量：向量是坐标系中的以原点为起点的有方向的箭头，其终点在坐标系的位置我们使用数字列表的形式表示出来（其实单个常数在线性代数中的主要作用就是用于缩放向量，例如坐标表示就是该数字缩放了对应基向量）

---

什么是线性组合

线性组合的概念

为方便叙述我们默认坐标系为二维坐标系，i为x轴基向量，j为y轴基向量

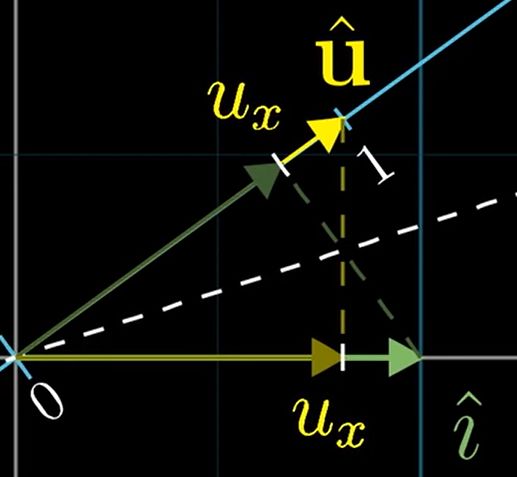
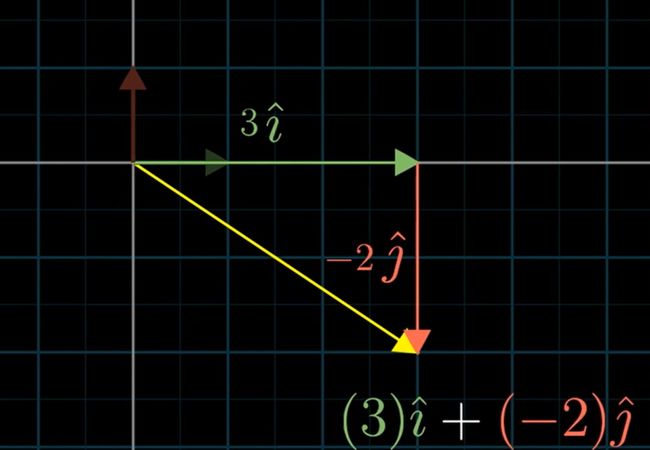
前面提到了向量表示，我们可以看作是向量坐标 放缩了对应的基向量并相加

两个数乘向量的和就称作两个向量的线性组合

空间的概念

给定基向量可以组成的所有线性组合的集合称作给定向量张成的空间。

因此大部分二维向量们张成的空间就是所有二维向量的集合（二维空间），而共线的二维向量张成的空间就是落在一条线上的向量的集合( 一维空间 )

线性相关的几何概念

线性相关和线性无关的判断的直接依据就是：是否每个向量都给张成的空间增加了维度。

向量不使张成空间增加维度 —> 则向量在落在该张成空间中 —> 张成空间是其他向量们所有线性组合的集合 —> 向量可以被其他向量线性表示出来 —> 该向量组是线性相关的

空间的基的定义

空间的一组基：就是张成该空间的线性无关向量的集合（每个决定该空间的维度的向量的集合）

---

什么是矩阵

总结：线性变换是一种操纵空间的手段，它直观上使得坐标系网格保持平行且等距分布进行变换，且这个变换只需要通过几个数字的组合（变换后的基向量坐标）就可以表示出来，这个数字的组合就是矩阵（即矩阵表示了一种线性变换）

什么是线性变换

变换 等价于 函数，函数大多是一个数经过函数的处理得到一个数，而线性变换是一个向量经过变换处理得到一个向量（变换是函数花哨的说法）（从一个向量变成另一个向量）

线性限定了变换的范围，变换可以非常复杂，既然是线性代数那我们就只讨论线性的变换。变换满足下面两个性质，就是线性的：

1. 直线在变换后仍是直线，不可弯曲

2. 坐标原点必须固定不动（若直线仍为直线，但坐标原点移动则为仿射变换）

线性变换的可视化理解

• 在充满网格的二维平面中，变换可以被可视化理解为：
  坐标系网格发生改变，从代表某一空间的坐标系网格图，变换为另一空间的坐标系网格图(因为该空间的每一个向量都进行了变换（即每一个向量从一个向量变成另一个向量）等同于整个空间都被进行了变换（即从一个空间变成另一个空间）)

• 在充满网格的二维平面中，线性变换的两个性质可被可视化理解为：
  使得 保持坐标系网格平行且等距分布 的变换

（线性变换需要保持网格平行很好理解，而理解为何要等距的平行，可以想象一条斜直线，若不等距变换会将其变成曲线）

总结线性变换的几何本质：

线性变换使得代变某一空间的网格图按照保持坐标系网格平行且等距分布的原则变化

线性变换的表达式 — 矩阵

首先我们由 “ 网格图按照保持坐标系网格平行且等距分布的原则变化” 可以得出一个重要推论：
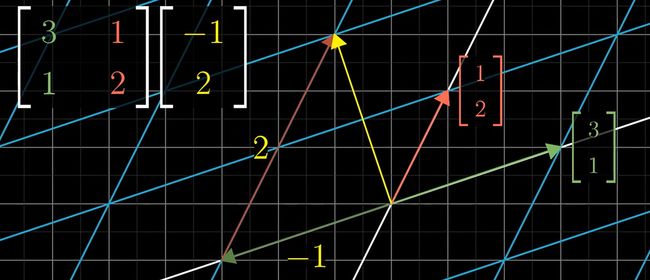
向量关于基的线性组合在变换前后是不改变的： v = -i + 2j / v ’ = -i ’ + 2j ’

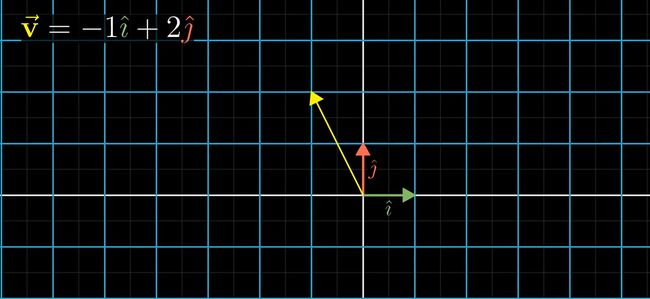
因此变换后的向量可以表示为：

因此：因为向量在线性变换中的线性组合不变（即基向量的缩放比例不变），我们只需要记录下变换后的基向量，就可以像上面那样算出，变换后的基形成的新向量的坐标！因此我们可以通过变换后的基向量组合就可以表示出这种线性变换 而这个变换后基向量的组合就是我们说的 矩阵 ！（我们往往可以通过矩阵中新基向量大致判断出这是一个怎样的线性变换）

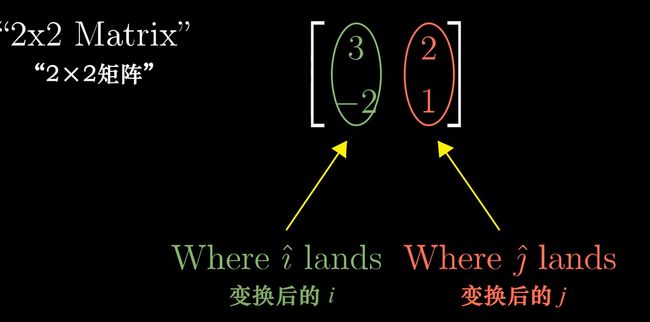
因此矩阵与向量相乘的几何意义就是：对该向量进行线性变换
(往往我们把向量中的数字看成是缩放基的标量)

---

什么是矩阵乘法

矩阵乘法的几何意义

由上文可知，矩阵是一种线性变换，若矩阵乘变量则会对变量进行线性变换。而矩阵乘矩阵，其实就是对一个线性变换进行线性变换，即线性变换的复合 （我们同样可以通过追踪基向量的变换来表示这种复合变换）

（注意：矩阵乘法从右到左读，就像复合函数 f ( g(x) ) ）

矩阵乘法运算上的几何意义

矩阵乘矩阵，是对一个线性变换进行线性变换，即对前一个线性变化的基分别进行线性变化

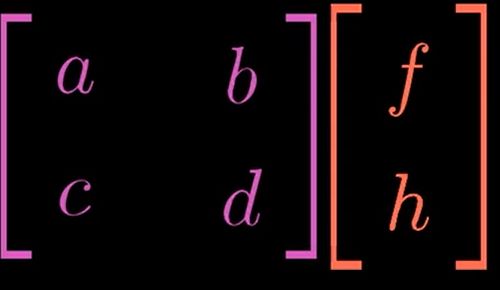
矩阵乘法的运算律的几何视角证明

无交换率 AB!=BA

易得矩阵乘法无交换律，因为易知线性变换的前后作用顺序不同造成的结果是不同的

有结合律 (AB) C = A (BC)

(AB) C —> C变换的基础上进行(AB)的复合变换，等价于C变换进行B变换再进行A变换（复合变换的几何意义）
A (BC) —> (BC)复合变换的基础上进行A变换，等价于C变换进行B变换再进行A变换（复合变换的几何意义）

因此二者都等价于 (ABC) ，即C变换先进行B变换再进行A变换

---

什么是行列式

行列式的几何意义

行列式表示的是一个线性变换对空间的挤压拉伸程度

矩阵的行列式的值 就是其代表的线性变换 对某一块空间(面积/体积)的 缩放比例

我们经常使用原基向量构成的1*1小方块作为基准来谈缩放比例，因为根据网格线平行且等距，1 *1小方块的缩放比例与其他所有特定的空间的缩放比例都相同

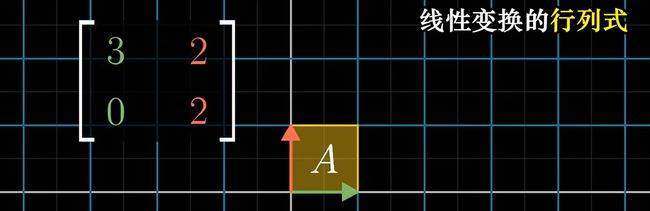
## 行列式为0的特殊情况：

（将空间的缩放比例为0，即降维）

行列式为负数的情况：

（基向量 i 和 j 的位置关系改变，空间的定向在线性变换中被改变，动态体现就是：空间在线性变换中转了个面）

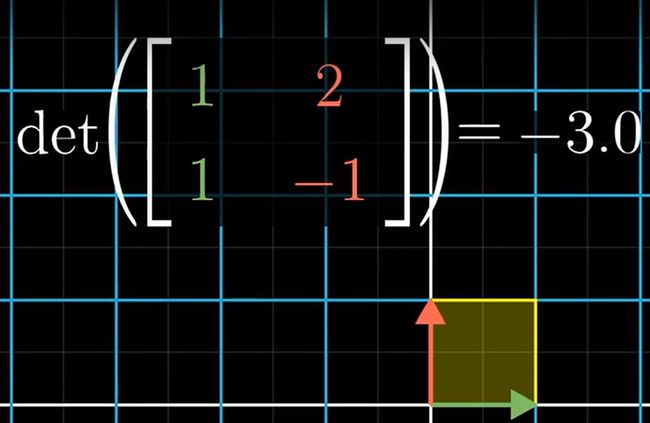
（二维中：一般基向量 i 在 j 的右边，如图变换后 i 在 j的左边，位置关系变换，空间的定向变换）

（三维中：空间的定向由右手法则判定）

---

什么是逆矩阵

线性方程组

线性代数之所以在很多个领域都会应用的主要原因是：它可以解特定的方程组（线性方程组）（注意：线性方程组中的方程只允许出现数乘和相加的操作，类似x²,sinx等式子是不能出现的）

线性方程组的求解可以写成矩阵与向量相乘等于一个向量的新形式

这样一来其线性方程组的几何意义就是：常数矩阵A将未知数向量 x经过线性变换后，与常数向量 v重叠

秩与列空间

秩（rank） — 描述线性变换后空间的维度大小。
eg: det(A) = 0, 当rank = 1时，A矩阵将空间压缩为一维直线，而当rank = 2时，A 矩阵将空间压缩为二维平面

列空间 — 矩阵的列空间是 矩阵所有可能的变换结果的集合（变为点,变为线,变为面等等）
（之所以称之为“ 列空间”的原因：矩阵所有可能变换出的空间，其实就是其列(基向量)张成的空间）

因此秩更准确的定义是：列空间的维度

秩与零空间

当秩达到最大值时，意味着秩与列数相等，称为满秩

原点处的情况：

1. 满秩矩阵下：
   由于线性变换中原点的位置不变，因此零向量在满秩矩阵的作用下仍位置不变，原点处只存在一个零向量 (满秩矩阵下唯一位置不变的向量)

2. 非满秩矩阵下：
   一系列的向量在降维的变换中变为零向量。原点处可能压缩了一个直线的向量甚至可能压缩了一平面的向量！
   经过矩阵变换后落在原点的向量构成矩阵的零空间或核

线性方程组的求解—逆矩阵

使用 Ax = v时有两种情况：

1. 当det（A）!= 0 ， 即线性变换未将空间降维,此时只存在一个对应的x，方程只有一个解

   这时在空间中只存在一个x我们可以通过倒带的方式由v找到x。

   这里说的倒带，其实指的是一种线性变换 — 逆矩阵 A^-1 ，(A^-1的核心是满足 A^-1A = I)

   此时x的解法为： A^-1Ax = A^-1 v —> x = A^-1 v

2. 当det（A）= 0 ， 即线性变换将空间降维，此时没有逆变换，但当向量x，v恰好同在降维上后的空间中时，那么解仍然存在

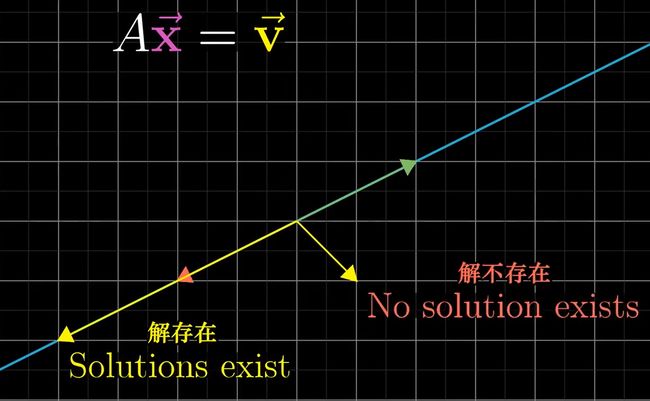
• 还有一种特殊的情况，当v 为零向量时，几何意义就是：x 变换后落在了零向量原点上，此时 x 就是矩阵的零空间

---

什么是点积

总结：向量的点乘中，向量对偶于一个高维到一维的线性变换

在向量1与向量2的点积中，向量1投影到向量2上，即有一个1*n降维矩阵使得向量1变换到向量2所在的直线上，而该矩阵的值恰为向量2的坐标值。故 矩阵1乘向量2 == 向量1点乘向量2

常见的点积几何意义解释：

点积是常用于解决向量指向和理解投影的有利几何工具

x • v 指 x在v上的投影 与 v 的乘积
（但是为什么点积会跟投影扯上关系呢 : )

将点积与线性变化相关联

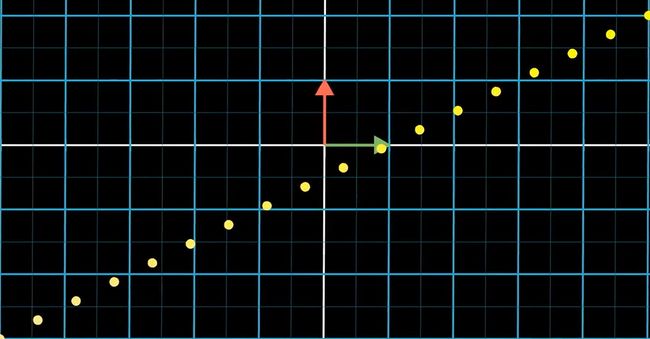
如图：当且仅当原本图像上相互等距的一系列点，落到数轴上后也是等距的，多维到一维(一维数轴，上图为x轴)的变换是线性变换。

---

现在解决 矩阵值和向量值相同， 接着往下思考：

1. 我们有x • v ，以v 所在的向量为我们降维变换后的数轴

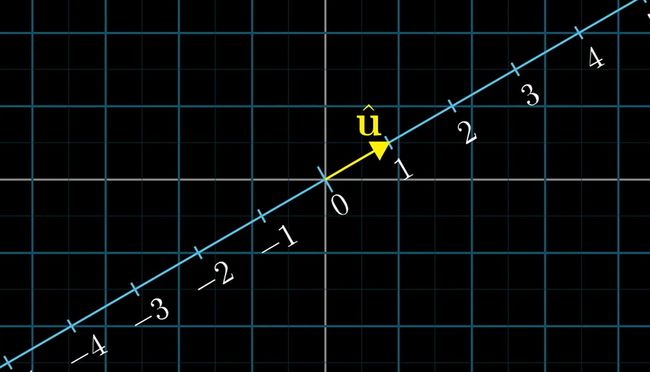
2. 为了求出该降维变换的矩阵，我们还是从基向量入手根据对称性原则，1*n矩阵的两元素 正是v 向量的坐标！

<------->

3. 故点乘x • v ，就是以 v向量坐标为矩阵元素的矩阵 对x 向量进行了线性变换(使x v共线) ，在图像上表现为，x线性变换至v所在直线上，即投影，在数值上表现为a * c + b *d，即向量对应相乘

启示：对偶性

向量的点乘中，向量对偶于一个高维到一维的线性变换

( 对偶性 ：即一种出乎意料但又自然的对应关系)

---

什么是基变换

核心在于：基的变换，就是通过矩阵进行的视角切换。

ps: 下文用别人的基（非默认基）和自己的基（默认基）来区分两套不同坐标系的基。

将她的基表示的坐标转换成自己的基表示

用自己的视角去看她的视角下的坐标的表示，使用自己视角下她的基向量组成的矩阵对她的向量进行线性变换就好

总结一下：通过自己的基表示她的基向量作为矩阵A，可以将 她的基表示的坐标翻译成自己的基表示的坐标

将自己的基表示的坐标转换成她的基表示

用她的视角看自己的视角下的坐标的表示，将上面的程序反过来（通过A的逆矩阵A^-1）对自己的向量进行线性变换就好

总结： 通过A^-1，可以将 自己的基表示的坐标 翻译成 她的基表示的坐标

非自己的基的坐标系进行线性变换

矩阵的线性变换有作用范围

首先先来看看自己的基的线性变换。我们的矩阵追踪记录的都是自己基，因此该矩阵只能对自己基的坐标系进行线性变换，而不能直接对别人的基坐标系进行线性变换

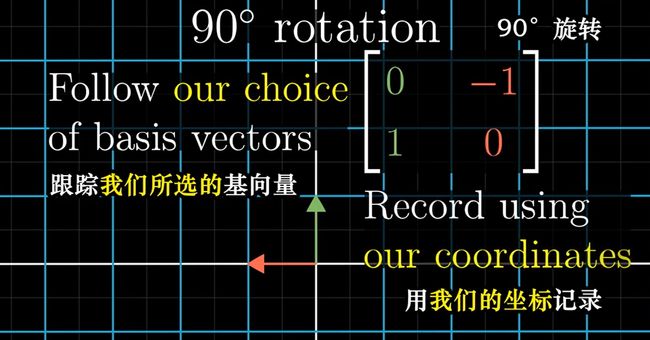
视角的转化

注意：A^-1MA 暗示着一种数学上的转移作用。M是你想进行的转移，而A,A^-1则有视角转化的作用。矩阵的转换仍是同一种变换（只不过是转化了角度，是在其它基的坐标系上进行的转换）

---

什么是特征向量和特征值

在以上所有知识的基础上，我们着手解决这个大问题。

一种特殊的性质和特征向量

有些向量在经过线性变换后，它留在原来向量张成的空间里。即线性变换对它来说仅仅就是一种缩放。

有这样特殊性质的向量就是特征向量

而每一个特征向量被缩放的比例就是特征向量的特征值

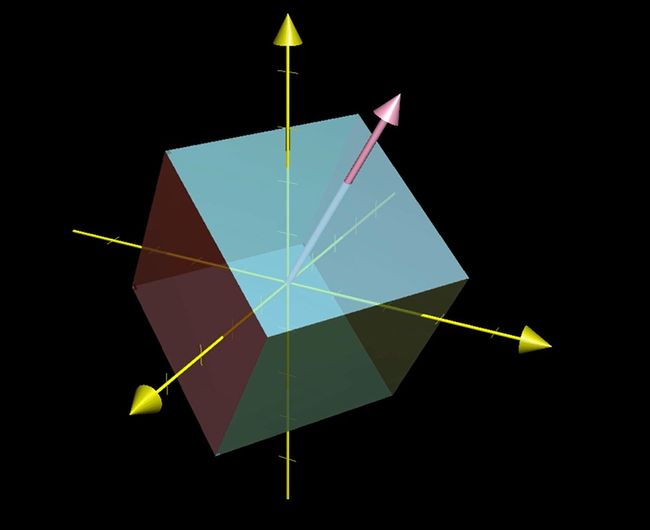
特征向量的几何意义

特征向量就是旋转轴！他能让你不过多依赖坐标系地去理解矩阵所代表的线性变换（若单单从基向量缩放去理解线性变换往往过度依赖坐标系）

特征向量中计算

计算时，将右边的 λ 常量化成 λ对角矩阵，使式子左右两边形式一致
即 Av = ( λI )v， 形式转换后就有 （A - λI )v = 0
这样一来我们需要矩阵（A - λI ) 能将 v压缩至原点（零空间），故需要由det(（A - λI )) = 0来求出λ，后求出满足条件的v

可能出现的情况 ：

1. 无特征值。如90°翻转
2. 单个特征值单个特征向量。如剪切变换
3. 单个特征值多个特征向量。如 坐标系全体倍增两倍变换
4. 多个特征值多个特征向量

特征基

当基向量为特征向量时称之为特征基（即基仅在原有的方向上进行缩放）

含特征基的线性变换，矩阵表示出来就是一个对角矩阵，矩阵的对角元是特征值。
换句话说：对角矩阵表示的是含特征基的线性变换

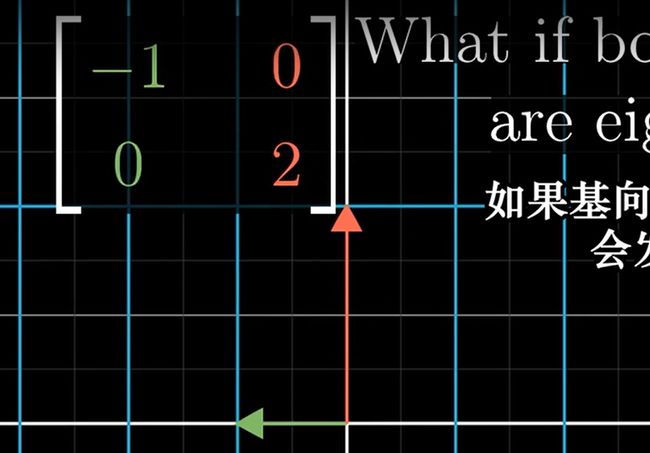
选用特征基构成的对角矩阵在计算时有极大的优势：

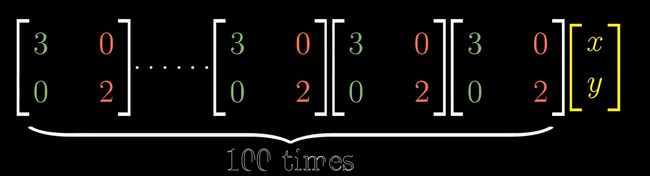
构成含特征基的线性变换

而当你有多个特征向量时，将原来的基转换为以特征向量为基，那么线性变换就成为了含特征基的变换。

因此为了使得线性变换称为含特征基的线性变换，我们使用基的A^-1MA转换式中，易知最后的结果一定是个对角矩阵

---

参考资料：

• 代数学引论(第1/2卷).(俄罗斯)柯斯特利金
• [youtube] 3Bule1Brown视频资料