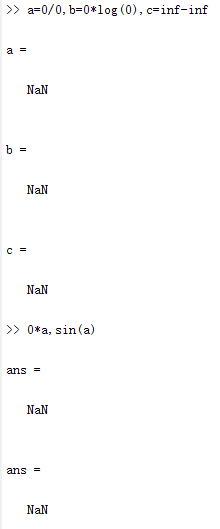MATLAB学习（二）数值数组及其运算
第二阶段学习正式开始！学习数值数组（Numeric Array）和数组运算（Array Operations）啦~（本小节学习例子较多干货满满，心疼本小仙笔记本的键盘菌三秒。记了这么多笔记，本小仙以后需要闭关修炼经常回顾！）
一维数组的创建和寻访
1、一维数组的创建
（1）采样数组x=a:inc:b
【说明】
（a）a是数组第一个元素；inc是采样点之间的间隔，即步长；生成数组的最后一个元素小于或等于b;
（b）a,inc,b之间必须用冒号“:”分隔。（注意:为英文冒号）；
（c）inc可以省略，默认取值为1；
（d）inc可以取正数和负数。
【eg.】
>> x=0:0.1:1 %定义自变量的采样点取值数组
>> y=x.*exp(-x) %利用数组运算计算各自变量采样点上的函数值
>> plot(x,y),xlabel('x'),ylabel('y'),title('y=x*exp(-x)') %绘图第一句指令，定义自变量采样数组x：以0为起点，每隔0.1取一个采样点，直到1为止。该数组x为（1*11）的数组。
第二句指令，指数函数对数组x每个元素求函数值，结果exp(x)也是一个（1*11）的数组，指令中的“.*”运算符：实施数组x和数组exp(x)中对应元素之间的相乘。因此，所得结果y也是（1*11）的数组。
第三句指令，plot根据所得到的的x数组和y数组，绘制曲线。数值计算都是关于采样数组进行的，因此，对于定义在连续区间上的函数，进行数值计算时必须对此给定的连续区间进行适当的采样，得到一个采样值数组。
（2）定数线性采样linspace
x=linspace(a,b,n)
【说明】
（a）生成数组的第一个元素为a，最后一个元素b。n是采样总点数。该指令产生（1*n）数组。
（b）该指令与x=a:(b-a)/(n-1):b作用相同。
（3）定数对数采样logspace
【说明】x=logspace(a,b,n)
（a）生成数组的第一个元素值为10^a，最后一个元素为10^b。n是采样总点数。该指令产生（1*n）数组。
（b）在信号处理和控制学科中，用该指令产生频率响应的频率自变量采样点。
2、子数组的寻访和赋值
【eg.1】寻访
>> rand('state',0) %把均匀分布伪随机发声器置为0状态 >> x=rand(1,5) %产生（1*5）的均匀分布随机数组 >> x(3) %寻访数组x的第三个元素 >> x([1 2 5]) %寻访数组x的第一、二、五个元素组成的子数组 >> x(1:3) %寻访前3个元素组成的子数组 >> x(3:end) %寻访除第三个元素起，至end最后一个元素。 >> x(3:-1:1) %由前三个元素倒排构成的子数组 >> x(find(x>0.5)) %由大于0.5的元素构成的子数组 >> x([1 2 3 4 4 3 2 1]) %对元素可以重复寻访，是所得数组长度允许大于原数组
【说明】
（a）寻访的子数组取决于数组x（index）的中下标index。
（b）end是一维数组中的长度，即最大下标。
图1 一维数组的寻访和赋值
【eg.2】赋值
>> x(3)=0 %把上例中第三个元素重新赋值为0 >> x([1 4])=[1 1] %把当前x数组的第一、四个元素都赋值为1
【说明】
要保证被重新赋值的子数组的长度与送入的数组长度相同。
二维数组的创建和寻访
1、二维数组的创建
（1）直接输入法
>> a=2.7358;b=33/79; %这两条指令分别给变量a,b赋值 >> C=[1,2*a+i*b,b*sqrt(a);sin(pi/4),a+5*b,3.5+i] %这指令用于创建二维数组C
【说明】
（a）整个数组必须用方括号[ ]为其首尾；
（b）数组的行与行之间必须用分号“；”或回车enter隔离；
（c）数组元素必须由逗号“，”或空格分隔。
（2）复数的数组
>> M_r=[1,2,3;4,5,6],M_i=[11,12,13;14,15,15] >> CN=M_r+i*M_i %由实部、虚部数组构成复数数组
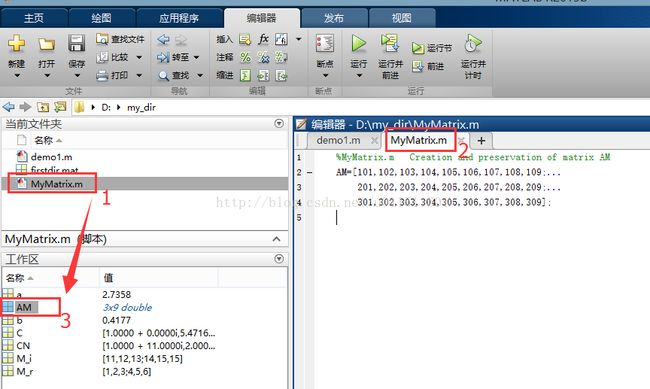
2、利用M文件创建和保存数组
%MyMatrix.m Creation and preservation of matrix AM AM=[101,102,103,104,105,106,107,108,109;... 201,202,203,204,205,206,207,208,209;... 301,302,303,304,305,306,307,308,309];
图2 利用M文件创建和保存数组
图3 运行MyMatrix.m文件，数组AM自动生成于MATLAB内存中
3、二维数组元素的标识
（1）逻辑数组的“逻辑1”标识
（a）逻辑数组（Logical Array）：L中元素或是0或是1；
（b）逻辑1标识法：通过与A同样大小的逻辑值数组L中“逻辑值1”所在的位置，指示A中元素的位置。
>> A=zeros(2,5); %预生成一个（2*5）全零数组 >> A(:)=-4:5 %运用“全元素”法向A赋值 >> L=abs(A)>3 %产生与A同维的“0-1”逻辑值数组 >> islogical(L) %判断L是否逻辑值数组。输出若为1，则是。 >> X=A(L) %把L中逻辑值1对应的A元素取出
图4 逻辑数组之“逻辑1标识”
（2）逻辑数组&双精度数组
>> Num=[1,0,0,0,1;0,0,0,0,1]; %产生与数组L外表完全相同的“双精度数组” >> N_L=Num==L %假如Num与L数值相等，则应等于1 >> c_N=class(Num) %用class指令检查Num的类属 >> c_L=class(L) %用class指令检查L的类属
图5 逻辑数组&双精度数组
4、二维数组的子数组寻访和赋值
| 子数组的寻访和赋值 | 使用说明 |
| A(r,c) | 它由A的“r指定行”和“c指定列”上的元素组成 |
| A（r，:) | 它由A的“r指定行”和“全部列”上的元素组成 |
| A(：,c) | 它由A的“全部行”和“c指定列”上的元素组成 |
| A(：) | “单下标全元素”寻访。它由A的各列按自左到右的次序，收尾相接而生成“一维长列”数组 |
| A(s) |
“单下标”寻访，生成“s指定的”一维数组。s若是“行数组”（或列数组），则A（s）是长度相同的“行数组”（或列数组） |
| A(L) | “逻辑1”寻访，生成“一维”列数组，与A相同大小的“逻辑数组”L中的“1”元素选出A对应元素；按“单下标”次序排成长列组成 |
| A(r,c)=Sa | 以“双下标”方式，对子数组A(r,c)进行赋值：Sa的长宽列长与A(r,c)的长宽列长相同 |
| A(:)=D(:) | 全元素赋值方式，结果保持A的长宽列长不变。条件：A、D两个数组的总元素数相等，但行宽列长不一定相同 |
| A(s)=Sa | 按“单下标”方式，对A的部分元素重新赋值，结果保持A的行宽列长不变。条件：s单下标数组的长度必须与“一维数组”Sa的长度相等，但是s、Sa不一定是同是“行数组”或“列数组” |
>> A=zeros(2,4) %创建（2*4）的全零数组 >> A(:)=1:8 %全元素赋值方式 >> s=[2 3 5] %产生单下标数组行数组 >> A(s) %由“单下标行数组”寻访产生A元素组成的行数组 >> Sa=[10 20 30]' %Sa是长度为3的“列数组” >> A(s)=Sa %单下标方式赋值 >> A(:,[2,3])=ones(2) %双下标赋值方式：把A的第2、3列元素全赋值为1
图6 二维数组的子数组寻访和赋值
执行数组运算的常用函数
执行数组运算的常用函数：
（1）三角函数和双曲函数：acos、asin、asec、cos、cot、sinh、tan......
（2）指数函数：exp、log、log10、log2、pow2（2的幂）、sqrt（平方根）
（3）复数函数：abs、angle、conj（复数共轭）、imag、real
（4）圆整函数和求余函数：ceil（向正无穷的圆整函数）、fix（向0圆整函数）、floor、mod（模除求余）、rem（求余数）、round（向最近整数圆整函数）、sign（符号函数）
（5）坐标变换函数：cart2sph（直角变球坐标）、cart2pol（直角变极坐标）、pol2cart（极坐标变直角）、sph2cart（球变直角坐标）
（6）特殊函数：erf（误差函数）、erfc（误差补）、erfcx（刻度误差补）、erfinv（逆误差补）、expint（指数积分）、gamma、gammainc（不完全伽马函数）、gammaln（伽马函数的对数）、isprime（质数为真函数）、rats（数值有理化函数）。
数组运算&矩阵运算
矩阵：一种变换或映射算子的体现；矩阵运算有着明确严格的数学规则。
数组运算：尚缺乏严谨的数学推理。
表2 列出两种运算指令形式和实质内涵
| 指令 | 数组运算 | 指令 | 矩阵运算 |
| A.' | conj(A')非共轭转置 | A’ | 共轭转置 |
| s.*A | 标量s分别于A的元素之积 | s*A | 标量s分别与A每个元素之积 |
| s-B，B-s | 标量s分别于B元素之差 | ||
| s./B，B.\s | s分别被B的元素除 | s*inv(B) | B矩阵的逆，乘s |
| A.^n | A的每个元素自乘n次 | A^n | A矩阵为方针时，自乘n次 |
| A.^p | 对A各元素分别求非整数幂 | A^p | 方针A的非整数乘方 |
| p.^A | 以p为底，分别以A的元素为指数求幂值 | p^A | A为方针时，标量的矩阵乘方 |
| A+B | 对应元素相加 | A+B | 矩阵相加 |
| A-B | 对应元素相减 | A-B | 对应元素相减 |
| A.*B | 对应元素相乘 | A*B | 内维相同矩阵的乘积 |
| A./B | A的元素被B的对应元素除 | A/B | A右除B |
| B.\A | 同上 | B\A | A左除B |
| exp（A） | 以自然数e为底，分别以A的元素为指数，求幂 | expm（A） | A的矩阵指数函数 |
| log（A） | 对A的各元素求对数 | logm（A） | A的矩阵对数函数 |
| sqrt（A） | 对A各个元素求平方根 | sqrtm（A） | A的矩阵平方根函数 |
| f（A） | 求A各个元素的函数值 | funm（A，'FN'） | 一般矩阵函数 |
| A#B | A、B矩阵对应元素间的关系运算；#代表关系运算符 | ||
| A@B | A、B矩阵对应元素间的逻辑运算；@代表逻辑运算符 | ||
| A=s | 把标量s赋给A的每个元素 | ||
| s+B | 标量s分别与B元素之和 | ||
【eg.】两种不同的转置
>> A=zeros(2,3) >> A(:)=1:6 %全元素赋值法 >> A=A*(1+i) %运用标量与数组乘产生复数矩阵 >> A_A=A.' %数组转置，即非共轭转置 >> A_M=A' %矩阵转置，即共轭转置
图7 数组运算&矩阵运算的两种不同转置
多项式的表达方式及其操作
1、 多项式表达方式
（1）降幂多项式P(x)=a1*x^n+a2*x^(n-1)+...+an*x+a(n+1)；
（2）用以下 系数行向量表示：P=[a1 a2 ... an a(n+1)]；
（3）利用指令：P=poly(AR)，产生多项式系数向量。
>> A=[11 12 13;14 15 16;17 18 19]; >> PA=poly(A) %A的特征多项式 >> PPA=poly2str(PA,'s') %以比较习惯的方式显示多项式
图8 求三阶方阵的特征多项式
2、 多项式运算函数
多项式运算函数的调用格式指令：
| 指令 | 含义 |
| p=conv(p1,p2) | p是多项式p1和p2的乘积多项式 |
| [q,r]=deconv(p1,p2) | 多项式p1被p2除的商多项式为q，而余多项式是r |
| p=ploy(AR) | 求方阵AR的特征多项式p；或求向量AR指定根所对应的多项式 |
| dp=polyder(p) | 求多项式p的导数多项式dp |
| dp=polyder(p1,p2) | 求多项式p1，p2乘积的导数多项式dp |
| [Num,Den]=ployder(p1,p2) | 对有理分式（p1/p2）求导数所得的有理分式为（Num/Den） |
| p=polyfit(x,y,n) | 求x,y向量给定的数据的n阶拟合多项式p |
| pA=polyval(p,S) | 按数组运算规则计算多项式值；p为多项式，S为矩阵 |
| PM=polyvalm(p,S) | 按矩阵运算规则计算多项式值；p为多项式，S为矩阵 |
| [r,p,k]=residue(b,a) | 部分分式展开：b、a分别是分子、分母多项式系数向量；r、p、k分别是留数、极点、直项 |
| r=roots(p) | 多项式p的根 |
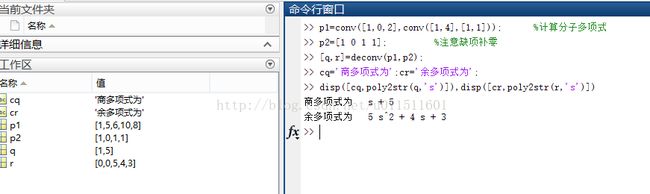
【eg.1】求“商”、“余”多项式
>> p1=conv([1,0,2],conv([1,4],[1,1])); %计算分子多项式 >> p2=[1 0 1 1]; %注意缺项补零 >> [q,r]=deconv(p1,p2); >> cq='商多项式为';cr='余多项式为'; >> disp([cq,poly2str(q,'s')]),disp([cr,poly2str(r,'s')])
图9 求“商”、“余”多项式
>> S=pascal(4) %生成一个4阶矩阵 >> P=poly(S) %求矩阵S的特征多项式 >> PA=polyval(P,S) %独立变量取数组S元素时的多项式值 >> PM=polyvalm(P,S) %独立变量取矩阵S时的多项式值
图10 两种多项式求值指令的差别
标准数组生成函数&数组操作函数
1、 标准数组生成函数
标准数组生成函数指令：diag(对角形)、eye（单位数组）、magic（魔方数组）、ones（全1）、rand（均分分布随机数组）、randn（正态分布随机数组）、zeros（全0数组）、gallery（产生特殊的测试矩阵）。
>> ones(1,2) %产生长度为2的全1行数组
>> ones(2,7) %产生2*7的全1数组
>> ones(2) %产生2*2的全1数组
>> randn('state',0) %把正态随机数发生器置为0
>> randn(2,3) %产生2*3的正态随机矩阵
>> D=eye(3) %产生3*3的单位阵
>> diag(D) %取D矩阵的对角元
>> diag(diag(D)) %取D矩阵的对角元，利用一维数组产生对角阵
>> repmat(D,1,3) %在水平方向“铺放”3个D阵2、 数组操作函数
数组操作函数 指令：cat（把大小相同的若干数组，沿“指定维”方向，串接成高维数组）、 diag（提取对角元素，生成对角阵）、flipdim（以指定维的对称轴进行翻转）、 fliplr（以数组“垂直中线”为对称轴，交换左右对称位置上的数组元素）、 flipud（以数组“水平中线”为对称轴， 交换上下对称位置上的数组元素）、kron（按Kronecker乘法规则产生“积”数组）、permute（按指定的次序，对矩阵各维的次序进行重组）、repmat（按指定维上的数目铺放模块数组）、 reshape（总元素数不变，改变各维的大小）、 rot90（逆时针旋转二维数组90度）、tril（下三角阵）、triu（上三角阵）。【eg.1】数组操作函数diag、reshape
>> a=-4:4 %采样数组：产生一维数组
>> A=reshape(a,3,3) %把一维数组a重新排成（3*3）的二维数组
>> a1=diag(A,1) %取A矩阵“第一上对角线”的元素
>> A1=diag(a1,-1) %产生以a1数组元素为“第一下对角线”元素的二维数组
图11 数组操作函数diag、reshape
【eg.2】数组转置、对称交换、旋转操作
>> A.' %转置
>> flipud(A) %上下对称交换
>> fliplr(A) %左右对称交换
>> rot90(A) %逆时针旋转90度
图12 数组转置、对称交换、旋转操作
>> A=reshape(1:9,3,3) %创建（3*3）数组A
>> A(5,5)=111 %扩展为（5*5）数组。其余补零。
>> A(:,6)=222 %标量对于子数组赋值，并扩展为（5*6）数组
>> AA=A(:,[1:6,1:6]) %相当于指令repmat(A,1,2)
>> B=ones(2,6) %创建（2*6）全1数组
>> AB_r=[A;B] %行数扩展合成
>> AB_c=[A,B(:,1:5)'] %列数扩展合成
>> A %重新显示A数组
>> AB_BA=triu(A,1)+tril(A,-1) %利用操作函数，使主对角元素全0
>> AB1=[A(1:2,end:-1:1);B(1,:)] %灵活合成
图13 多次寻访扩展、合成扩展
A=reshape(1:16,2,8) %变为（2*8）数组
reshape(A,4,4) %变为（4*4）数组
s=[1 3 6 8 9 11 14 16] %定义“单下标”数组
A(s)=0 %利用“单下标”数组对A的元素重新赋值
图14 单下标寻访、reshape指令
>> A=reshape(1:9,3,3)
>> b=[1 2 3]
>> A_b1=A-b([1 1 1],:) %使A的第1,2,3行分别减b向量[1 2 3]
>> A_b2=A-repmat(b,3,1)
>> A_b3=[A(:,1)-b(1),A(:,2)-b(2),A(:,3)-b(3)]
图15 对列（行）同加一个数（3种操作方法）
>> randn('state',1)
>> R=randn(3,6) %创建正态随机库、
>> L=abs(R)<0.5|abs(R)>1.5 %不等式条件运算，结果给出逻辑数组
>> R(L)=0 %逻辑1对应的元素赋0值
>> s=(find(R==0))' %利用find获得符合关系等式条件的元素单下标
>> R(s)=111 %利用“单下标”定位赋值
>> [ii,jj]=find(R==111); %利用find获得符合关系等式条件的元素“双下标”
>> disp(ii'),disp(jj')
图15 逻辑函数的运用
高维数组
1、高维数组的创建
创建高维数数组最常用的4种方法是：
（1）直接通过通过“全下标”元素赋值方式创建高维数组；
（2）由若干同样大小的低维数组组合成高维数组；
（3）由函数ones、zeros、rand、randn直接创建标准高维数组；
（4）借助cat、repmat、reshape等函数构作高维数组。
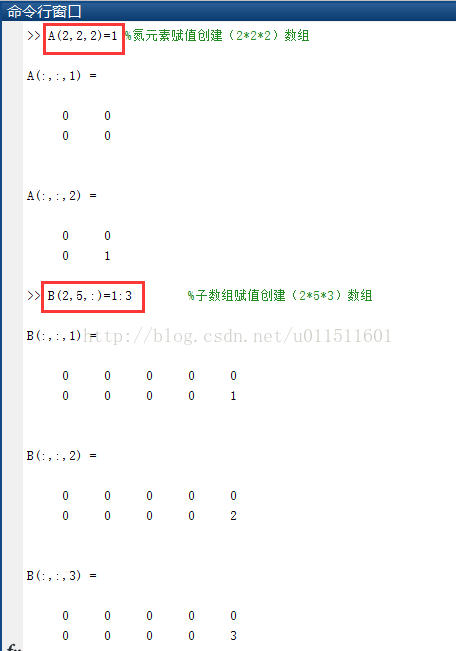
【eg.1】“全下标”元素赋值方法创建高维数组
>> A(2,2,2)=1 %单元素赋值创建（2*2*2）数组
>> B(2,5,:)=1:3 %子数组赋值创建（2*5*3）数组
图16 “全下标”元素赋值方法创建高维数组
【eg.2】低维数组合成高维数组
>> A=ones(2,3);
>> A(:,:,2)=ones(2,3)*2;
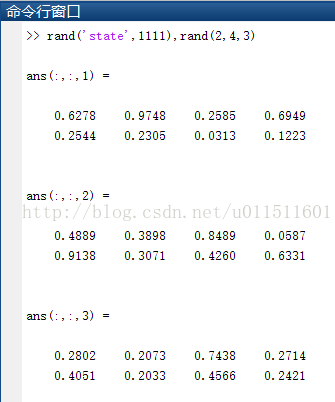
>> A(:,:,3)=ones(2,3)*3
图17 低维数组合成高维数组
【eg.3】由函数ones、zeros、rand、randn直接创建标准高维数组
>> rand('state',1111),rand(2,4,3)
图18 rand直接创建标准高维数组
【eg.4】借助cat、repmat、reshape等函数构作高维数组
【说明】
（1）cat指令：第一个输入量表示“表示串接方向的维号”，本例“3”，表示“沿第三维方向串接”。
（2）repmat指令：第一个输入量“模块数组”。第二个输入量“各维方向”铺放“模块数组”的数目。本例“[1,1,3]”表示：在“行维方向”、“列维方向”各铺1块，而在“页维方向”铺3块。
（3）reshape指令：第一个输入量“待重组”的数组，第二、三、四输入量是要生成的数组的“行数、列数、页数”。
>> cat(3,ones(2,3),ones(2,3)*2,ones(2,3)*3)
>> repmat(ones(2,3),[1,1,3])
>> reshape(1:12,2,2,3)
图19 借助cat、repmat、reshape等函数构作高维数组
2、高维数组的标识
（1）数组的维数和ndims指令
“行”数组（或称向量）是一维数组，即“维数为1”。而矩阵是二维数组，即“维数为2”。
指令ndims(A)：直接给出数组A的维数。
（2）数组的大小和size指令
不管A数组的维数是多少，
指令size(A)：给出A各维的大小，
指令 length(A)：给出所有维中的最大长度。length(A)等价于max(size(A))。
【eg.1】获取数组A的维数、大小和长度信息
>> dim_A=ndims(A) %测量A的维数
>> size_A=size(A) %测量A的大小
>> L_A=length(A) %求A的长度
图20 获取数组A的维数、大小和长度信息
3、高维数组构作&操作函数
高维数组操作函数&标准数组生成函数：
| 指令 | 含义 |
| cat | 把“大小”相同的若干数组，沿“指定维”方向，串接成高维数组 |
| flipdim | 以指定“维的平分面”，交换对称位置上的元素 |
| ipermute | 广义反转置，permute的反操作 |
| ones | 产生全1数组 |
| permute | 广义非共轭转置 |
| rand | 产生均匀分布随机数组 |
| randn | 产生正态分布随机数组 |
| repmat | 按指定维上的数目铺放模块数组，以形成更大的数组 |
| reshape | 总元素数不变，改变各维大小 |
| shiftdim | 数组的“维序号左移”重组 |
| squeeze | 撤销长度为1的“孤维”，使数组降维 |
| zeros | 产生全0数组 |
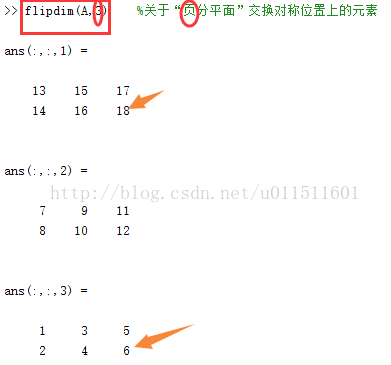
【说明】指令 flipdim(A,k)：第一个输入量A为备操作的数组，第二个输入量k为指定对称面。“1”表示与数组“行”平行的平分面；“2”表示与数组“列”平行的平分面；“3”表示与“数组页”平行的平分面。
>> A=reshape(1:18,2,3,3) %创建三维数组
>> flipdim(A,1) %关于“行分平面”交换对称位置上的元素
>> flipdim(A,2)
>> flipdim(A,3) %关于“页分平面”交换对称位置上的元素
图21 数组元素对称交换指令flipdim
重组运算 B=shiftdim(A,1)：维序号左移 1位，实现 b(i,j,k)=a(j,k,i)；
重组运算 B=shiftdim(A,2)：维序号左移 2位，实现 b(i,j,k)=a(k,i,j)；
>> shiftdim(A,1) %“维号左移1位”重组，使（2*3*3）数组变成（3*3*2）数组
>> shiftdim(A,2) %“维号左移2位”重组，使（2*3*3）数组变成（3*2*3）数组
图22 数组的“维序号左移”重组 shiftdim
【说明】指令 permute：第一个输入量是被转置数组，第二个输入量是指定转置方法的行数组。
permute操作更为一般，实现“维序号”任意排列。
>> permute(A,[2,3,1]) %相当于shiftdim(A,1)
>> permute(A,[1,3,2])
图23 广义非共轭转置
>> B=cat(4,A(:,:,1),A(:,:,2),A(:,:,3)) %串接为4维数组
>> size(B) %测量数组B大小
>> C=squeeze(B) %撤销长度为1的“孤维”，使原4维数组减为3维数组
>> size(C)
图24 “孤维”的撤销和降维
【eg.5】赋“空阵”值操作
>> A=reshape(1:18,2,3,3) %创建3维数组
>> A(:,2:3,:)=[] %赋“空”，使原A数组的第二、三列消失
>> B=A;
>> size(A)
>> A_1=squeeze(A) %撤销“孤维”，数组由3维降为2维
>> size(B) %B数组与A同样存在“孤维”
>> B(:,1,:)=[] %对“孤维”赋“空”，不能降维
图25 赋“空阵”值操作
“非数”NaN&“空”数组
0/0、无穷/无穷、0*无穷等运算都会产生 非数NaN（Not a number）。性质：（1）传递性（2）不可比较性（3）不能进行关系运算（4）属性判断 isnan(a)（5）非数元素的寻访
【eg.1】非数
>> a=0/0,b=0*log(0),c=inf-inf
>> 0*a,sin(a)
>> a=nan %该指令想计算“a等于非数吗”，但不能得到正确结果
>> a==nan %该指令想计算“a等于非数吗”，但不能得到正确结果
>> a~=nan %该指令想计算“a不是非数吗”也不能得到正确判断结果
>> a==b %两个非数不存在“等、不等”概念
>> b>c %两个非数不能比较大小
>> class(a) %数据类型归属
>> isnan(a) %该指令是唯一能正确判断非数的指令
>> rand('state',0) %将随机发生器置0，方便把自己运算结果与本书对照
>> R=rand(2,5);R(1,5)=NaN;R(2,3)=NaN %创建带非数的二维数组
>> isnan(R) %判断数组元素是否非数
>> Linear_index=find(isnan(R)) %非数“单下标”标识
>> [r_index,c_index]=ind2sub(size(R),Linear_index); %转换成“全下标”标识
>> disp('r_index c_index'),disp([r_index c_index])
图26 非数
【eg.2】“空”数组
某维长度为0或若干维长度均为0的数组就是“空”数组。判断数组是否为“空”数组指令isempty。“空”数组在运算中不具备传递性，可以对其他非空数组赋值，可以收缩数组的大小，不能改变那数组的维数。
“空”数组：（1）创建（2）“空”数组的属性（3）不具备传递性（4）不可比较（5）
>> a=[ ],b=ones(2,0),c=zeros(2,0),d=eye(2,0),f=rand(2,3,0,4)
>> class(a) %“空”数组的数据类别
>> isnumeric(a) %判断是否为数值数据类
>> isempty(a) %唯一正确判断是否为空的指令
>> which a %变量a是什么
>> ndims(a) %数组a的维数
>> size(a) %a数组的大小
>> b_c1=b.*c %两个空阵的点乘
>> b_c2=b'*c %生成矩阵为0*0,故为空
>> b_c3=b*c' %生成矩阵2*2
>> a==b %不等于
>> b==c %无法比较
>> c>d %无法比较
>> a==0 %不等于
>> a~=0 %是不等
>> A=reshape(-4:5,2,5) %创建一个数值数组A
>> L2=A>10 %检查A中大于10的元素位置
>> find(L2) %找出L2逻辑数组中非0元素的“单下标”标识
>> A(:,[2,4])=[] %删除A的第二、三列
图27 “空”数组
关系操作&逻辑操作
1、关系操作
所有关系表达式&逻辑表达式的计算结果，即由0和1组成的“逻辑数组（Logical Array）”，在此数组中的1为真，0为假。【eg.】关系运算运用：求近似极限，利用非数NaN修补图形缺口。
>> t=-2*pi:pi/10:2*pi; %该自变量数组中，存在0值
>> y=sin(t)./t; %在t=0处，计算将产生NaN
>> tt=t+(t==0)*eps; %逻辑数组参与运算，使0元素被一个“机器零”小数代替
>> yy=sin(tt)./tt; %用数值计算的sin(eps)/eps近似替代sin(0)/0极限
>> subplot(1,2,1),plot(t,y),axis([-7,7,-0.5,1.2]),xlabel('t'),ylabel('y'),title('残缺图形')
>> subplot(1,2,2),plot(tt,yy),axis([-7,7,-0.5,1.2]),xlabel('t'),ylabel('yy'),title('正确图形')
图28 关系运算之求近似极限
2、逻辑操作
三组逻辑操作：
（1）数组逻辑操作：&（与）、|（或）、~（非）、xor（相异返回1，相同返回0）
（2）二进数位逻辑操作：bitand（数位与）、bitor（数位或）、bitcmp（数位非）、bitxor（相异数位返回1、相同数位返回0）
（3）先决逻辑操作：&&（若运算符左边的被运算量是“假”，则不再观察运算符右边的被运算符，立刻给出运算结果为“假”）、
||（若运算符左边的被运算量是“真”，则不再观察运算符右边的被运算符，立刻给出运算结果为“真”）
3、表达式各种运算符的优先级
| 优先级（高-->低） | 运算符 | |||||
| 1 | 括号（） | 共轭转置' | 数组幂.^ | 矩阵幂^ | ||
| 2 | 转置.' | 代数负- | ||||
| 3 | 代数正+ | 数组除./ | 矩阵乘* | 矩阵左除\ | 矩阵右除/ | |
| 4 | 数组乘.* | 减- | ||||
| 5 | 加+ | |||||
| 6 | 冒号： | 大于> | 等于== | 不小于> | 不大于<= | 不等于~= |
| 7 | 小于< | |||||
| 8 | 数组与& | |||||
| 9 | 数组或| | |||||
| 10 | 先决与&& | |||||
| 11 | 先决或|| |
特殊函数：isempty（x）、isfinite（x）、isinf（x）、isletter（x）中英文字母为1、isnan（x）非数为1、isprime（x）质数为1、isreal（x）实数为1、isspace（x）空格为1.
数据类型判断：isa（x,'name'）是指定name的数据类型为1、iscell（x）是元胞为1、ischar（x）、ishandle（x）是图柄代号为1、isstruct（x）是结构为1...
状态判断：ishold处于保留为1、isstudent是学生版本为1、isieee是计算机执行IEEE算法规则为1.
楼下大叔，求别锁门！.........