baidu进阶训练笔记九20200727

第五章 百度Apollo规划技术介绍（二）

motion planning with environment-1

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2xVYjvpB-1595839029378)(C:\Users\xiaomeiyan\AppData\Roaming\Typora\typora-user-images\image-20200727154450553.png)]

Vehicle state and model

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FoXykx8U-1595839029381)(C:\Users\xiaomeiyan\AppData\Roaming\Typora\typora-user-images\image-20200727154751465.png)]

对于汽车而言，质点模型是远远不够的，无人车是前轮转向的车，前后位置的变化是不一样的，那么怎么去描述这种不一样呢？首先从刚体角度考虑，二维平面里的刚体涉及到XY和θ，也就是以车后轴中心作为XY坐标原点时车身的朝向heading。因为无人车运动模型还多了一个转向的变量，多了一个自由度，刚体模型也不够。

Motion planning with vehicle models

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-B65aKrFr-1595839029384)(C:\Users\xiaomeiyan\AppData\Roaming\Typora\typora-user-images\image-20200727155018527.png)]

两个轮子在转动的时候是沿着同一个中心转动的

后轮的转向半径1/κ与方向盘转动角度ω满足以下关系，其中L为前轮中心和后轮中心的距离。κ=(tan(ω))/L

Describe the motion of bicycle model

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-zTLSky7o-1595839029387)(C:\Users\xiaomeiyan\AppData\Roaming\Typora\typora-user-images\image-20200727155233553.png)]

在实际的自行车运动模型中，后轴中心是沿着如上图所示的一条平滑的轨迹运行，该轨迹对应的曲率κ 表示调整方向盘的度数，如果为正，表示向左转，反之则向右转。

SL coordinate Frame and XY Coordinate Fram

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Gh45jY71-1595839029387)(C:\Users\xiaomeiyan\AppData\Roaming\Typora\typora-user-images\image-20200727155414212.png)]

S表示道路中心线的方向，L表示与道路中心线垂直的方向

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-S1Rh4e5u-1595839029388)(C:\Users\xiaomeiyan\AppData\Roaming\Typora\typora-user-images\image-20200727155545270.png)]

SL坐标系到XY坐标系的投影：之所以要投影到世界坐标系，是因为很多信息是全局的，例如红绿灯位置，参考的是XY世界坐标系。在给定SL坐标系时，每一个点的S坐标本身对应一个（x-r，y-r）坐标，根据该点的横向偏移距离，可以求出给定点在世界坐标系中的XY位置

XY Frame to SL Frame

XY坐标系到SL坐标系的投影：因为SL坐标系并不是唯一的，XY会在曲线上产生很多投影，投影点是经过XY坐标，且垂直于曲线的线段与曲线的交点

• 怎样找到一个mapping?

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2wVCE4co-1595839029390)(C:\Users\xiaomeiyan\AppData\Roaming\Typora\typora-user-images\image-20200727160147676.png)]

判断有没有sign changes

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-xLVDxe8v-1595839029392)(C:\Users\xiaomeiyan\AppData\Roaming\Typora\typora-user-images\image-20200727160230663.png)]

SL to XY —> 判断障碍物之间的关系

超平面分割定理

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-I7CnD5vW-1595839029394)(C:\Users\xiaomeiyan\AppData\Roaming\Typora\typora-user-images\image-20200727160443571.png)]

降低维度判断是否相交

motion planning with environment-2

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rqWX1BBb-1595839029395)(C:\Users\xiaomeiyan\AppData\Roaming\Typora\typora-user-images\image-20200727160903140.png)]

无限连续无限平滑，道路中心线要平滑（curvature要连续）

不能单独smooth一个curvature，要根据动力学模型做平滑

龙格现象

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mQgISliE-1595839029397)(C:\Users\xiaomeiyan\AppData\Roaming\Typora\typora-user-images\image-20200727161228882.png)]

在轨迹上以等距离的方式随机选择一些点，然后用高阶多项插值的方式来近似表示轨迹，对多项式进行优化。但是高阶多项式不能用于平滑，因为高阶的多项式抖动太大，没有办法控制幅度

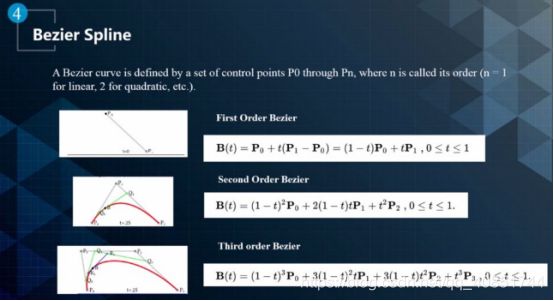
Bezier Spline

Bezier Spline 曲线是由一系列控制点定义的，例如P0 到 Pn，其中n代表曲线的阶数。如图所示，分别给出1阶、2 阶、3 阶 Bezier Spline 曲线的表示形式。通过对它们做平滑，得到平滑的曲线，例如二阶平滑保证曲线的曲率平滑。但是这种方法的缺点是，除了起始点和终点，其它控制点不能保证会被得到的曲线经过。

2DConstrained Smoothing Spline

抽象点、控制点、生成一条光滑曲线、满足约束条件

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-o21psBtM-1595839029398)(C:\Users\xiaomeiyan\AppData\Roaming\Typora\typora-user-images\image-20200727161528116.png)]

一维平滑方法

最短路径，但是路径最短还不能保证平滑性，因此会对其不同阶导数进行 Minimize 求解，保证导数空间的连续

• Smoothing Spline 的特殊的性质
  • 在给定边界的条件下，它是一个多项式，可以找到最优解。前提是它的 Boundary Constraint 只考虑了起点和终点，如果中间有障碍物就不是最优解。这种情况下可以使用 Piecewise Polynomial（分段多项式）来处理。
  • 一个 Piecewise Polynomial 是一维的函数，描述二维曲线是不够的，这时候就有一个 Spline 2D，假设我们把曲线分成 N 截，每节曲线段它的 X 坐标是一个 Polynomial ，Y 坐标也是一个 Polynomial 。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-X8D0bhXk-1595839029400)(C:\Users\xiaomeiyan\AppData\Roaming\Typora\typora-user-images\image-20200727162110860.png)]

建立平滑的坐标系

把曲线分为n节线段，每一节都是一个polynomial函数

怎么让曲线足够平滑？我们让它在 X 坐标上的变化率，也就是三阶导的平方是最小的，Y 上的变化率三阶导也是最小的，代价函数就是这两个变化率的和。代价函数的求解就是一个二次规划问题，我把这种 Loss Function 定义成这种形式是因为平方的积分能够给计算带来便利。

• 端点的约束条件要保证连接点之间，对x方向的导数和对y方向的导数都要是相等的，三阶导连续会带来很多好处，还要满足约束条件

螺旋曲线

• 通过一个极坐标形式定义，比如说沿着一条曲线，如果一个点 S 的曲率是知道的，假设它的原点在 （0，0）的位置，可以唯一定义出一条经过 S 的曲线，也就是 Spiral Path 。那么可以让 Spiral Path 满足起点、终点约束条件生成一条螺旋曲线。

Spiral Path 和 Spline 2D 的区别呢？

• 任何的曲线在足够密的时候都可以用Piecewise Spiral path 或者是 Piecewise Polynomial 表示。
• 区别：出发点不一样
  • Polynomial 计算很快很简单，Spline 2D 是一个凸空间里面生成一个 Spline 曲线。
  • Spiral Path 是从 Configuration Space 出发。理论上来讲，螺旋曲线生成的线是要比 Spiral Path 更好处理，对一些极端情况处理更好。