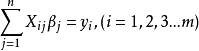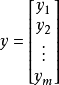奇异矩阵 最小二乘法
什么是奇异矩阵:
首先奇异矩阵是方阵,其次方阵的行列式不为0.如果行列式为0,则是奇异矩阵,如果行列式不为0,则不是奇异矩阵,行列式不为0,是可逆矩阵。
最小二乘法:
之前接触过,没太仔细看,也许是没有理解,最小二乘法是用来求函数方程中未知参数的方法,也可以用来拟合函数。在机器学习中,监督方法中,如果需要预测的变量是离散的,则是分类,像决策树方法,支持向量机方法,如果预测的变量是连续的,则是属于回归,一个自变量一个因变量,且能用一条直线来表示的是一元线性回归,多个自变量,一个因变量且能用线性表达的是多元线性回归。
利用最小二乘法的步骤,先设未知变量,根据给出的数据集列方程,最小化均方误差,列出方程之后对要求的参数求偏导,偏导为0解出要求的参数值。
最小二乘法成立的前提是假设均方误差服从正态分布。
对于多元函数的参数求取:
线性最小二乘的基本公式
编辑
考虑超定方程组(超定指未知数小于方程个数):
其中m代表有m个等式,n代表有 n 个未知数
![]()
,m>n ;将其进行向量化后为:
![]()
显然该方程组一般而言没有解,所以为了选取最合适的
![]() ,让该等式"尽量成立",引入残差平方和函数S。
,让该等式"尽量成立",引入残差平方和函数S。![]()
(在统计学中,残差平方和函数可以看成n倍的均方误差MSE)
当 ![]() 时,
时, ![]() 取最小值,记作:
取最小值,记作:![]()
通过对 ![]() 进行微分 [2] 求最值,可以得到:
进行微分 [2] 求最值,可以得到:
![]()
如果矩阵 ![]() 非奇异则
非奇异则 ![]() 有唯一解 [3] :
有唯一解 [3] :
![]()