最近公共祖先LCA
Part 1:了解LCA
\(LCA\)(Least Common Ancestors),中文翻译是“最近公共祖先”

(原图来自洛谷)
对于给定的一棵树和这棵树的树根(如上图)
给定两个节点,他们的最近公共祖先(以下简称\(LCA\))就是这两个点分别到树根的简单路径中经过的所有点的交集中,深度最深的一个
以上面的图为例子,点对\((3,5)\)的\(LCA\),我们按照定义来求:
\(step 1\):求出\(3\)到树根的路径是\(3 \rightarrow 1 \rightarrow 4\)
\(step 2\):求出\(5\)到树根的路径是\(5 \rightarrow 1 \rightarrow 4\)
所以点对\((3,5)\)的\(LCA\)就是点\(1\)
Part 2:\(LCA\)的求法
\(LCA\)的定义很好理解,相信大家很容易就明白了,现在我们讨论怎么求两个节点的\(LCA\)
法一:向上标记法
向上标记法是最简单的求\(LCA\)的暴力算法
算法主要思路:对于两个给定节点\((a,b)\),我们任意挑选一个,这里我们假设选择\(a\)节点
\(step 1:\)从\(a\)节点到树根一个一个节点的遍历,对遍历到的节点进行标记
\(step 2:\)从\(b\)节点到树根一个一个节点的遍历,如果遍历到一个被标记的节点,那么这个点就是点对\((a,b)\)的\(LCA\)
向上标记法既是按照定义求\(LCA\)——求出简单路径交集的最深节点
但是这是一个赤裸裸的暴力,它的复杂度是\(O(n)\),其中\(n\)是点的深度
但是对于一棵比较高大威猛的树来说,仅仅线性的复杂度显然不够优秀,所以代码就不再给出了,我们考虑优化
法二:倍增求\(LCA\)
还是考虑给定一棵树和根节点,求树上点对\((a,b)\)的\(LCA\)
上面的算法慢的主要原因是每次仅仅向上标记\(1\)个节点,那么我们想到了倍增算法,每次向上跳\(2^k\)个点
如果想实现这个算法,我们就得记录每个点向上\(2^k\)步的父节点,我们可以用如下的预处理方式解决
预处理:记录各个点的深度和他们\(2^i\)级的的祖先,用数组\(\rm{depth}\)表示每个节点的深度,\(fa[i][j]\)表示节点\(i\)的\(2^j\) 级祖先。
\(LCA\) \(prework\) \(code:\)
void dfs(int now, int fath) { //now表示当前节点,fath表示它的父亲节点
fa[now][0] = fath; depth[now] = depth[fath] + 1;
for(int i = 1; i <= lg[depth[now]]; ++i)
fa[now][i] = fa[fa[now][i-1]][i-1];
//这个转移可以说是算法的核心之一
//意思是now的2^i祖先等于now的2^(i-1)祖先的2^(i-1)祖先
//原理显而易见,根据初中数学,可以得到这个式子:2^i = 2^(i-1) + 2^(i-1)
for(int i = head[now]; i; i = e[i].nex)
if(e[i].t != fath) dfs(e[i].t, now);
}
然后是怎么倍增的问题,如果我们拿到点对\((a,b)\)就直接开始向上跳的话,由于初始时\(a,b\)的深度不一样,这样使得跳跃步数难以控制,增大了思维量(其实几乎不可做。
为了解决这个问题,我们考虑先把\(a,b\)中深的那一个跳到浅的那一个同一深度,然后一起向上倍增跳跃,这样我们对于边界条件的处理会方便许多
调整深度也很简单,我们假设\(a\)的深度大于\(b\)的深度,那么先把\(a\)向上跳\(2^k\)步,如果到达的深度比\(b\)浅,那么尝试跳\(2^{k-1}\)步,以此类推,直到跳到与\(b\)的深度相等
调整完了,下面是倍增求\(LCA\)的步骤
\(step 1:\)把\(a,b\)调整到同一深度的祖先后,如果这两个点相同,说明其中深度浅的是\(LCA\),如果不同,执行\(2\)
\(step 2:\)如果他们的\(2^k\)祖先是同一个点,说明跳多了,我们就“反悔”,看看\(2^{k-1}\)是不是同一个点,如果不是同一个点,就向上跳\(2^{k-1}\)步
\(step 3:\)重复\(2\),直到跳到某一个深度,此时\(a\)和\(b\)的父节点重合了,那么这个父节点就是所求\(LCA\)
倍增求\(LCA\)核心代码:
inline int LCA(int x, int y) {
for(int i=1; i<=n; i++){
lg[i]=lg[i-1];
if(i==1<= y的深度
swap(x, y);
while(depth[x] > depth[y])
x = fa[x][lg[depth[x]-depth[y]] - 1]; //先跳到同一深度,方便处理
if(x == y) //如果x是y的祖先,那他们的LCA肯定就是x了
return x;
for(int k = lg[depth[x]] - 1; k >= 0; --k)
if(fa[x][k] != fa[y][k]) //因为我们要跳到它们LCA的下面一层,所以它们肯定不相等,如果不相等就跳过去。
x = fa[x][k], y = fa[y][k];
return fa[x][0]; //返回父节点
}
这样查询\(LCA\)的复杂度是\(O(logn)\)其中\(n\)是点的深度,比向上标记法快了不少
剩下的建树就不用讲了吧,用邻接表然后把上面的代码copy一下直接调用LCA()函数即可
法三:\(RMQ\)(Range Minimum/Maximum Query)求LCA
算法原理
其实,这种做法算的上是一个奇技淫巧吧
先普及一个小知识点:欧拉序(怎么又是欧拉
(其实我尝试过自己画图但是真的太丑了所以还是用洛谷的图叭
欧拉序,其实和深度优先遍历序(先序遍历)非常的相似:
为了方便大家理解,我们先写出这棵树的\(dfs\)序:\(4,2,1,3,5\)
那么我先写出欧拉序,然后再解释:\(4,2,4,1,3,1,5,1,4\)
大家可能已经看出来了,欧拉序其实就是\(dfs\)序在回溯时又重新记录了一下遍历的点而已
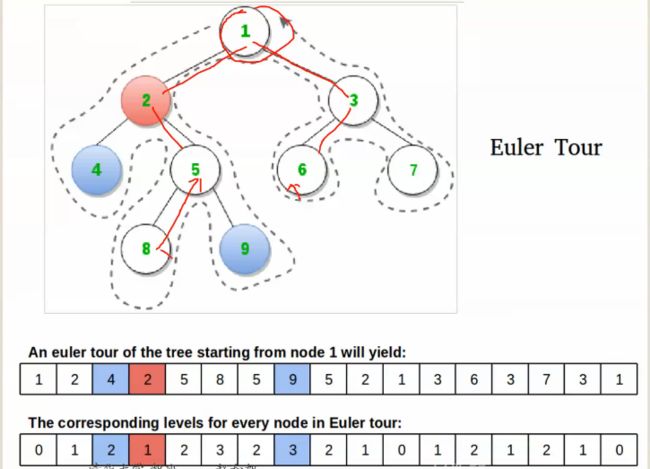
现在给出这样一张图:
图中给出了一棵以\(1\)为根的树,下面的第一个序列是欧拉序,第二行是欧拉序中各点在树中的深度(深度序)
我们发现一个有趣的现象——我们查询\(x,y\)的\(LCA\)其实就是在深度序中\(x\)的下标和\(y\)的下标之间的最小值的下标在欧拉序中所对应的节点
如果上面的语言描述不够简洁,我们用严格的数学语言描述一遍:
\(1、\)找到查询点\(x,y\)在欧拉序中找到这两个点第一次出现的下标,记作\(l,r\)。
\(2、\)在深度序上对区间\([l,r]\)上查询最小值,记下标为\(qwq\)
\(3、\)那么\(x,y\)的\(LCA\)就是欧拉序中下标为\(qwq\)的点
是不是很玄学奇妙,又比倍增\(LCA\)更加易于理解呢?
这个算法的核心原理在于:对于欧拉序遍历,任意一棵非空子树的根节点一定在其所有儿子节点的前面和后面各出现一次,而根节点的深度一定比儿子节点的深度浅,那么两个点之间出现的深度最小值就是这棵子树的根节点,也就是包含\(x,y\)最小子树的根节点,同时也是他们的\(LCA\)
预处理
\(1、\)欧拉序当然要先预处理啦!同时为了保证珂爱的复杂度不被破坏,我们还要记录第\(i\)个点在欧拉序中的下标,这样我们单点查询欧拉序下标的时候就是\(O(1)\)而不是遍历的\(O(n)\)
\(2、\)深度序,表示第\(i\)个点在\(dfs\)中的层数,这个可以在求欧拉序的时候顺便求出来
预处理\(Code\):
void dfs(const int x,const int depth){
vis[x]=1;//标记一下已经走过x号节点
dis[id]=depth;//id是迭代器,depth为当前深度
eula[id][0]=x;//记录欧拉序
if(eula[x][1]==0) eula[x][1]=id;//这一维代表第i个点的欧拉序下标
id++;//完成记录后迭代器++
for(unsigned int i=0;i下面的问题将变成一个赤裸裸的\(RMQ\)问题,对于\(RMQ\)问题我们有一大堆优秀的算法,比如\(st\)表,线段树……等等都是优秀的\(RMQ\)算法
由于弱,我选择了使用建树和查询都是\(log\)级且自带大常数的线段树来求\(RMQ\)
求出了\(RMQ\)之后,我们把这个下标对应到欧拉序中,输出即可
蒟蒻代码展示:
#include
#include
#include
#include
#include
#include
#include 好了,今天关于\(LCA\)算法的分享就到这里了(跪求三连