斯坦福cs231n课程记录——assignment2 BatchNormalization
目录
- BatchNormalization原理
- BatchNormalization实现
- BatchNormalization运用
- Layer Normalization
- 参考文献
一、BatchNormalization原理
先敬大佬的一篇文章《详解深度学习中的Normalization,BN/LN/WN》
运用:to make each dimension zero-mean unit-variance.
算法:
(最后需要scale and shift 是因为上一步进行零均值单位方差化后数据都在0周围,这样特征是比较难学的,所以需要重新缩放和平移,使其趋于一个真实的分布)
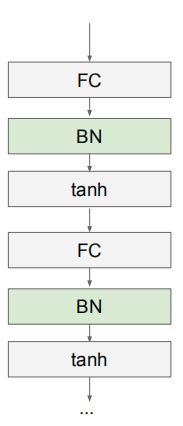
位置:Usually inserted after Fully Connected or Convolutional layers, and before nonlinearity.
(From : cs231n_2018_lecture06)
三、BatchNormalization实现
算法:
正向传播:
def batchnorm_forward(x, gamma, beta, bn_param):
"""
Input:
- x: Data of shape (N, D)
- gamma: Scale parameter of shape (D,)
- beta: Shift paremeter of shape (D,)
- bn_param: Dictionary with the following keys:
- mode: 'train' or 'test'; required
- eps: Constant for numeric stability
- momentum: Constant for running mean / variance.
- running_mean: Array of shape (D,) giving running mean of features
- running_var Array of shape (D,) giving running variance of features
Returns a tuple of:
- out: of shape (N, D)
- cache: A tuple of values needed in the backward pass
"""
mode = bn_param['mode']
eps = bn_param.get('eps', 1e-5)
momentum = bn_param.get('momentum', 0.9)
N, D = x.shape
running_mean = bn_param.get('running_mean', np.zeros(D, dtype=x.dtype))
running_var = bn_param.get('running_var', np.zeros(D, dtype=x.dtype))
out, cache = None, None
if mode == 'train':
########################################################
mu = np.mean(x, axis=0) #均值
sigma2 = np.var(x, axis=0) #方差
x_hat = (x - mu) / np.sqrt(sigma2 + eps)
out = gamma * x_hat + beta #scale & shift
########################################################
running_mean = momentum * running_mean + (1 - momentum) * mu
running_var = momentum * running_var + (1 - momentum) * sigma2
inv_sigma = 1. / np.sqrt(sigma2 + eps)
cache = (x, x_hat, gamma, mu, inv_sigma)
elif mode == 'test':
x_hat = (x - running_mean) / np.sqrt(running_var + eps)
out = gamma * x_hat + beta
else:
raise ValueError('Invalid forward batchnorm mode "%s"' % mode)
# Store the updated running means back into bn_param
bn_param['running_mean'] = running_mean
bn_param['running_var'] = running_var
return out, cache反向传播:(红色部分推导为第二种简化算法)
def batchnorm_backward(dout, cache):
"""
Inputs:
- dout: Upstream derivatives, of shape (N, D)
- cache: Variable of intermediates from batchnorm_forward.
Returns a tuple of:
- dx: Gradient with respect to inputs x, of shape (N, D)
- dgamma: Gradient with respect to scale parameter gamma, of shape (D,)
- dbeta: Gradient with respect to shift parameter beta, of shape (D,)
"""
dx, dgamma, dbeta = None, None, None
x, x_hat, gamma, mu, inv_sigma = cache
N = x.shape[0]
dbeta = np.sum(dout, axis=0)
dgamma = np.sum(x_hat * dout, axis=0)
dvar = np.sum(-0.5 * inv_sigma ** 3 * (x - mu) * gamma * dout, axis=0)
dmu = np.sum(-1 * inv_sigma * gamma * dout, axis=0)
dx = gamma * dout * inv_sigma + (2 / N) * (x - mu) * dvar + \
(1 / N) * dmu
return dx, dgamma, dbetadef batchnorm_backward_alt(dout, cache):
"""
Alternative backward pass for batch normalization.
For this implementation you should work out the derivatives for the batch
normalizaton backward pass on paper and simplify as much as possible. You
should be able to derive a simple expression for the backward pass.
See the jupyter notebook for more hints.
Note: This implementation should expect to receive the same cache variable
as batchnorm_backward, but might not use all of the values in the cache.
Inputs / outputs: Same as batchnorm_backward
"""
dx, dgamma, dbeta = None, None, None
x, x_hat, gamma, mu, inv_sigma = cache
N = x.shape[0]
dbeta = np.sum(dout, axis=0)
dgamma = np.sum(x_hat * dout, axis=0)
dxhat = dout * gamma
dx = (1. / N) * inv_sigma * (N * dxhat - np.sum(dxhat, axis=0) -
x_hat * np.sum(dxhat * x_hat, axis=0))
return dx, dgamma, dbetadx difference: 7.494857050222097e-13
dgamma difference: 0.0
dbeta difference: 0.0
speedup: 1.40xdx由于在公式化简所以存在一些浮点误差。
该方法(batchnorm_backward_alt)比原始方法(batchnorm_backward)快1.4倍。
四、BatchNormalization运用
4.1 Fully Connected Nets with Batch Normalization
4.2 Batchnorm for deep networks
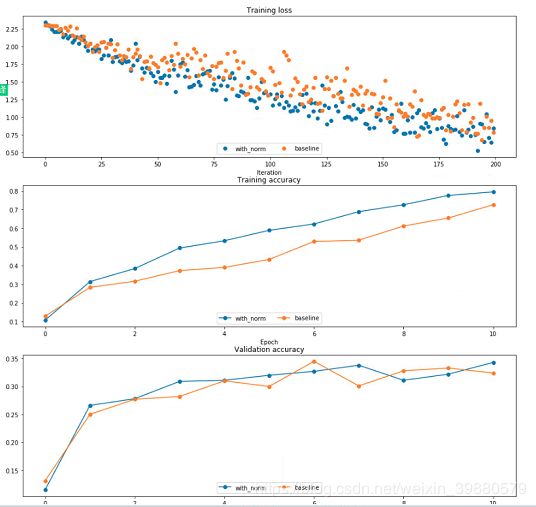
We can find that using batch normalization helps the network to converge much faster.
4.3 Batch normalization and initialization
Inline Question 1:
Describe the results of this experiment. How does the scale of weight initialization affect models with/without batch normalization differently, and why?
Answer:
bn 对权重初始化的scale容忍性更大,当scale比较小的时候,bn有着更好的效果,能够更快的收敛,同时也能防治梯度爆炸,因为bn会将每一层的输出重新normalize。
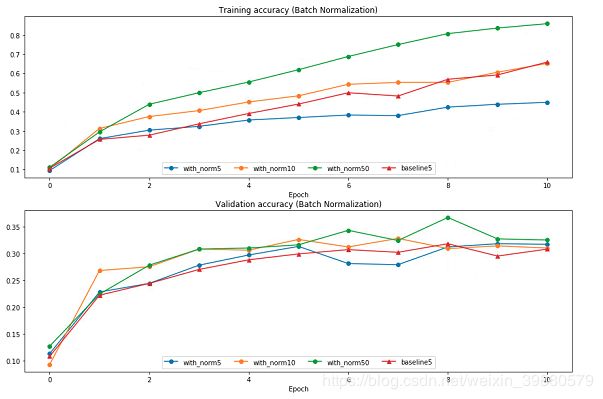
4.4 Batch normalization and batch size
Inline Question 2:
Describe the results of this experiment. What does this imply about the relationship between batch normalization and batch size? Why is this relationship observed?
Answer:
当batch size比较小的时候,bn的训练准确率会比较低,因为在训练的时候,bn使用的是一个batch中的统计量,所以存在统计量计算不准的问题,在batch较小的时候尤为明显,当batch比较大的时候,效果就会更好,但是在测试模式下这个问题并不明显,因为测试模式的时候使用的是running统计量,近似于数据的全局统计量,所以在测试模式下,batch size对bn就没有影响了。
是朋友,就不要让自己的兄弟用大于32的mini-batch!(该篇文章正确与否尚未论证)
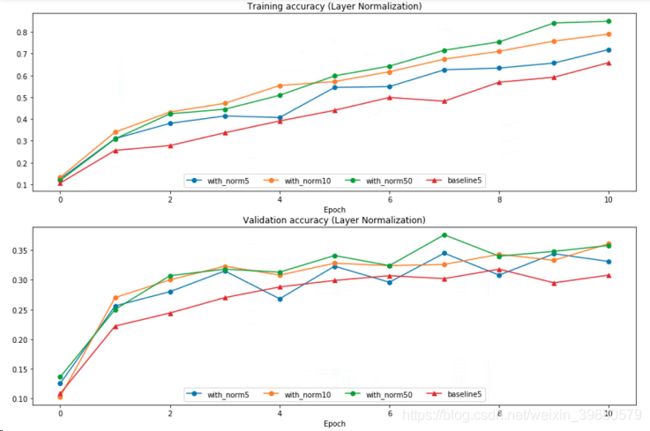
五、Layer Normalization
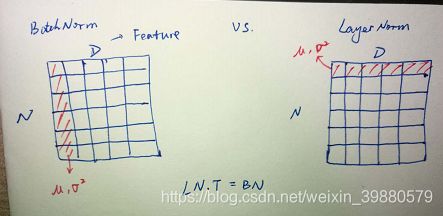
Batch normalization has proved to be effective in making networks easier to train, but the dependency on batch size makes it less useful in complex networks which have a cap on the input batch size due to hardware limitations.
Layer Normalization是以feature 计算的,所以对batch size 的容忍度更高,bach size 比较小时可以用。
Inline Question 3:
Which of these data preprocessing steps is analogous to batch normalization, and which is analogous to layer normalization?
- Scaling each image in the dataset, so that the RGB channels for each row of pixels within an image sums up to 1.
- Scaling each image in the dataset, so that the RGB channels for all pixels within an image sums up to 1.
- Subtracting the mean image of the dataset from each image in the dataset.
- Setting all RGB values to either 0 or 1 depending on a given threshold.
Answer:
1 和 2 类似于 layernorm,3 类似于 batchnorm
def layernorm_forward(x, gamma, beta, ln_param):
"""
Input:
- x: Data of shape (N, D)
- gamma: Scale parameter of shape (D,)
- beta: Shift paremeter of shape (D,)
- ln_param: Dictionary with the following keys:
- eps: Constant for numeric stability
Returns a tuple of:
- out: of shape (N, D)
- cache: A tuple of values needed in the backward pass
"""
out, cache = None, None
eps = ln_param.get('eps', 1e-5)
x = x.T # (D, N)
mu = np.mean(x, axis=0) # (N,)
sigma2 = np.var(x, axis=0) # (N,)
x_hat = (x - mu) / np.sqrt(sigma2 + eps) # (N, D)
x_hat = x_hat.T
out = gamma * x_hat + beta
inv_sigma = 1 / np.sqrt(sigma2 + eps)
cache = (x_hat, gamma, mu, inv_sigma)
return out, cachedef layernorm_backward(dout, cache):
"""
Backward pass for layer normalization.
For this implementation, you can heavily rely on the work you've done already
for batch normalization.
Inputs:
- dout: Upstream derivatives, of shape (N, D)
- cache: Variable of intermediates from layernorm_forward.
Returns a tuple of:
- dx: Gradient with respect to inputs x, of shape (N, D)
- dgamma: Gradient with respect to scale parameter gamma, of shape (D,)
- dbeta: Gradient with respect to shift parameter beta, of shape (D,)
"""
dx, dgamma, dbeta = None, None, None
x_hat, gamma, mu, inv_sigma = cache
d = x_hat.shape[1] # (N, D)
dgamma = np.sum(dout * x_hat, axis=0)
dbeta = np.sum(dout, axis=0)
dxhat = (dout * gamma).T
x_hat = x_hat.T
dx = 1. / d * inv_sigma * (d * dxhat - np.sum(dxhat, axis=0) -
x_hat * np.sum(dxhat * x_hat, axis=0))
dx = dx.T
return dx, dgamma, dbetaInline Question 4:
When is layer normalization likely to not work well, and why?
- Using it in a very deep network
- Having a very small dimension of features
- Having a high regularization term
Answer:
2 会使得layer normalization受到影响,主要是因为layer normalization在每一层的所有神经元上求统计量,如果神经元的维度太小,可能会导致统计量差异太大从而模型性能波动太大。
参考文献
[1]《Sergey Ioffe and Christian Szegedy, "Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift", ICML 2015.》
[2] Ba, Jimmy Lei, Jamie Ryan Kiros, and Geoffrey E. Hinton. "Layer Normalization." stat 1050 (2016): 21.

![\hat{x}^{(k)} =\frac{x^{(k)} - E[x^{(k)}]}{ \sqrt{Var[x^{(k)}]}}](http://img.e-com-net.com/image/info8/856f21fb7ee543d2b409f17dc5452fe7.gif)