UPC 2020年春混合个人训练第十四场

问题 A: 物理课（模拟）
时间限制: 1 Sec 内存限制: 128 MB

题目描述
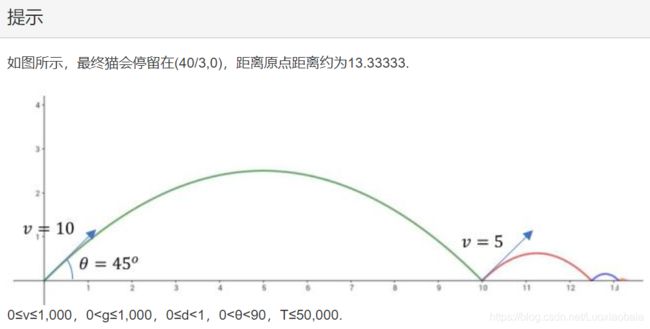
wzy正在上物理课！他发现了一个完全不会的题目：caoxia在一个奇妙的星球上（重力加速度为g）踢了一只猫，猫飞起的路线与地面夹角为θ（角度制），初速度为v，猫非常地开心，所以每次落地后会自己反弹，但反弹后速度会乘以一个常数d(0≤d<1)。请问猫最后的落点离起点多远？
（猫飞行时方向不会改变，飞行过程中不计空气阻力与摩擦力，所有数值单位均为国际标准单位制）
输入
第一行一个数T，代表有T组数据。接下来T行每行4个浮点数，分别为θ,v,d,g，保留到小数点后两位。
输出
共T行，每行一个浮点数表示猫离起点的距离，四舍五入到5位小数。
样例输入 Copy
3
45 10 0.5 10
3.44 2.35 0.77 1.76
2.33 2.33 0.78 9.8
样例输出 Copy
13.33333
0.92330
0.11493

题解：首先把速度分解为向上大小为 cos(90-θ) * v 的速度和向前为 cosθ * v 的速度设为 x , y，则一次的距离为 t*v=2xy/g，记为S。题目求

等比数列求和一下 ：ans=S/(1-d^2)【注意cos里面是弧度】。

#include
#define db double
using namespace std;
int T;
db th,v,d,g;
int main()
{
    cin>>T;
    while(T--){
        scanf("%lf%lf%lf%lf",&th,&v,&d,&g);
        db x=cos(th/180*M_PI)*v,y=cos((90-th)/180*M_PI)*v; //分别求出水平和竖直方向上的初速度
        db tmp=x*y*2/g; //求出 1次的距离
        tmp=tmp/(1-d*d); //用等比数列求和公式求出所有距离之和
        printf("%.5lf\n",tmp);
    }
    return 0;
}

问题 B: 数学课（模拟）
时间限制: 1 Sec 内存限制: 128 MB

题目描述
wzy又来上数学课了……虽然他很菜，但是数学还是懂一丢丢的。老师出了一道题，给定一个包
含n个元素的集合P={1,2,3,…,n}，求有多少个集合A⊆P，满足任意x∈A有2x∉A，且对于A在P中的补集B，也满足任意x∈B有2x∉B。wzy花费了1E100天终于算出来了这个答案，但是可恶的caoxia居然又加了一个条件！他要求A的大小恰好为m，这样又有多少个A呢？
这回wzy真的不会了，他找到了你，希望能够得到帮助。由于答案太大，你只需要输出答案mod 10000019即可。
输入
第一行两个数，为n,q。接下来q行每行一个数m，询问大小为m的A一共有多少个。
输出
共q行，每行一个数，表示方案数 mod 10000019.
样例输入 Copy
3 3
0
1
2
样例输出 Copy
0
2
2
提示
样例解释：P={1,2,3}，A可以选{1},{2},{1,3},{2,3}，大小为1的两种，大小为2的也有两种。
n,m≤1018,q≤100,000.

em…好伐，这题暂时没法AC，仅在本地运行，样例正确，这段时间找个机会求助大佬，把它给AC了

#include 
#define LL long long
using namespace std;
const int mod=10000019,N=mod+1;
int k,fac[N]={1,1},ifac[N]={1,1},inv[N]={0,1},q;
LL n,m,lian[101],mnlen,mxlen,odd,even,a;
int mul(int a,int b){return 1ll*a*b%mod;}
int lucas(LL a,LL b){
	if(b>a)return 0;
	if(!b||a==b)return 1;
	if(a<mod&&b<mod)return mul(mul(fac[a],ifac[b]),ifac[a-b]);
	return mul(lucas(a/mod,b/mod),lucas(a%mod,b%mod));
}
int ksm(int a,LL b){int ret=1;for(;b;b>>=1,a=mul(a,a))if(b&1)ret=mul(ret,a);return ret;}
void pre(LL n){
	for(int i=2;i^mod;++i)inv[i]=mul(inv[mod%i],mod-mod/i),fac[i]=mul(fac[i-1],i),ifac[i]=mul(ifac[i-1],inv[i]);
	int num=0;
	while(n){
		++num;a=n>>1;
		if(a&1)lian[num]+=(n-a)>>1;
		else lian[num]+=(n-a+1)>>1;n>>=1;
		mnlen+=lian[num]*(num/2);
		mxlen+=lian[num]*((num+1)/2);
		(num&1?odd:even)+=lian[num];
	}
}
int main(){
	scanf("%lld%d",&n,&q);pre(n);
	while(q--){
		scanf("%lld",&m);
		if(m>mxlen||m<mnlen){puts("0");continue;}
		printf("%d\n",mul(lucas(odd,m-mnlen),ksm(2,even)));
	} 
}

问题 D: TRPS买水果（模拟）
时间限制: 1 Sec 内存限制: 128 MB

题目描述
炎热的夏天自然有水果相伴。Tac想吃西瓜，Pod想吃荔枝，Rej想吃那猴桃，但是他们约计价方式各有不同，其中西瓜A银币1魄罗，荔枝B银币1奎罗．
猿猴桃C银币1个，其中单位1魄罗＝2奎罗。
要买x魄罗西瓜，y魄罗荔枝，z个猿猴桃，需要多少银币．
输入
一行6个整数A,B,C.x,y,z。
输出
一行一个整数表示需要的银币数
样例输入 Copy
5 6 7 1 2 3
样例输出 Copy
50
提示
A,B,C,x,y,z≤1000000000

**大水题 **

#include 
#define ll long long 
using namespace std;
ll  A,B,C,x,y,z,ans;
int main()
{
	scanf("%lld%lld%lld%lld%lld%lld",&A,&B,&C,&x,&y,&z);
	ans=x*A+2*B*y+C*z;
	cout<<ans;
	return 0;
}

问题 G: chess（搜索/组合数学）
时间限制: 1 Sec 内存限制: 128 MB

题目描述
小Q是A国的圣骑士。
A国与B国之间的一场恶战，令无数勇士战死沙场。战争已持续近两个多月，作为圣骑兵团的队长，小Q也发现了对方阵营的战术布局：
B国的军阵是一个大小为n×m的矩阵，每一个位置有一个士兵。特别的是，其中有恰好k名长矛手，两个长矛手不会在同一行或者同一列，否则他们就会失去控制而自相残杀。
现在，作为圣骑团的团长，小Q想知道对方有多少种排布军阵的方式，以便研究相应的战术，一举击垮敌人。
输入
共一行三个整数n,m,k，含义如题所述。
输出
一行一个整数，表示对方军阵的方案数。
样例输入 Copy
3 2 2
样例输出 Copy
6
提示
对于30%的数据，满足n,m,k≤4。
对于另外30%的数据，满足n=m=k。
对于100%的数据，满足n,m,k≤15

题解： 这题可以用 dfs 来写，直接搜，也可以用组合数学的基本知识来写（打表）【注意：这题很容易超限，所以我们都用数组来存储（理解并牢记这些数组累乘的小技巧，熟练了就能直接敲 ！）】。

// G(组合数学)
#include 
#define ll long long 
using namespace std;

ll n,m,k,c[1005][1005],a[1005];

int main(){
   c[0][0]=1;
   for(int i=1;i<=15;i++) {
   	   c[i][0]=1;
   	   for(int j=1;j<=i;j++)
   	   	    c[i][j]=c[i-1][j]+c[i-1][j-1]; //组合数性质2：C(m,n)=C(m-1,n)+C(m-1,n-1)[ C(m,n)表示n下m上,在这里 i代表 n]
   } 
   
   a[0]=1;
   for(int i=1;i<=15;i++) a[i]=a[i-1]*i;
   
   cin>>n>>m>>k;
   printf("%lld\n",c[n][k]*c[m][k]*a[k]);
   return 0;
}