Kmeans和DBSCAN聚类算法实战

1.问题描述
      对beer数据集进行分簇。①针对于Kmeans方法，首先将数据集分成2个和3个簇，查看一下结果；然后对数据集的特征进行标准化，对比了为标准化的结果；最后通过设置不同的簇的数量，来查看聚类效果。②针对于DBMSAN方法，通过设置不同的eps邻域半径和核心对象最小的阈值min_samples两个参数的值，来观察聚类效果。
2.Kmeans聚类算法

# beer dataset
import pandas as pd
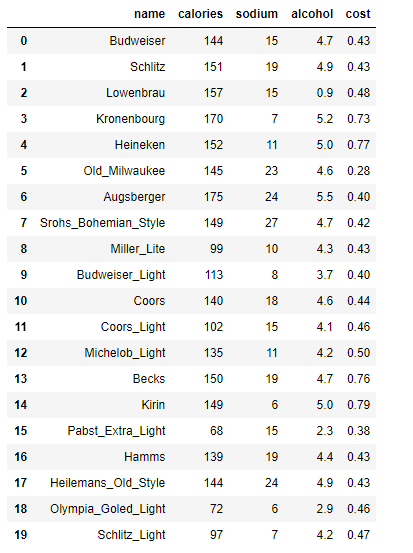
beer = pd.read_csv('data.txt',sep=' ')
beer

 X = beer[["calories","sodium","alcohol","cost"]]

2.1将数据集分别分成2和3个簇

from sklearn.cluster import KMeans
km = KMeans(n_clusters = 3).fit(X)
km2 = KMeans(n_clusters=2).fit(X)

添加新的列，即每条数据所归属的簇的id

beer['cluster'] = km.labels_
beer['cluster2'] = km2.labels_

获得聚类中心

from pandas.plotting import scatter_matrix
%matplotlib inline
cluster_center = km.cluster_centers_
cluster_center2 = km2.cluster_centers_

用各个簇的特征平均值来表示中心的所有特征值

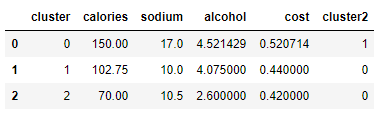
centers = beer.groupby('cluster').mean().reset_index()
centers

%matplotlib inline
import matplotlib.pyplot as plt
plt.rcParams['font.size'] = 14

import numpy as np
colors = np.array(['red','green','blue','yellow'])

对scatter_matrix函数的参数进行说明
      1）frame:pandas dataframe对象
      2）alpha: 图像透明度，一般取(0,1]
      3）figsize:以英寸为单位的图像大小，一般以元组 (width, height) 形式设置
      4）ax:可选一般为none
      5）diagonal:必须且只能在{‘hist’, ‘kde’}中选择1个，’hist’表示直方图(Histogram plot),’kde’表示核密度估计(Kernel Density
Estimation)；该参数是scatter_matrix函数的关键参数
      6）marke:Matplotlib可用的标记类型，如’.’，’,’，’o’等
      7）density_kwds(other plotting keyword arguments，可选)，与kde相关的字典参数
      8）hist_kwds与hist相关的字典参数
      9）range_padding(float, 可选)，图像在x轴、y轴原点附近的留白(padding)，该值越大，留白距离越大，图像远离坐标原点
      10）kwds与scatter_matrix函数本身相关的字典参数
      11）c:颜色

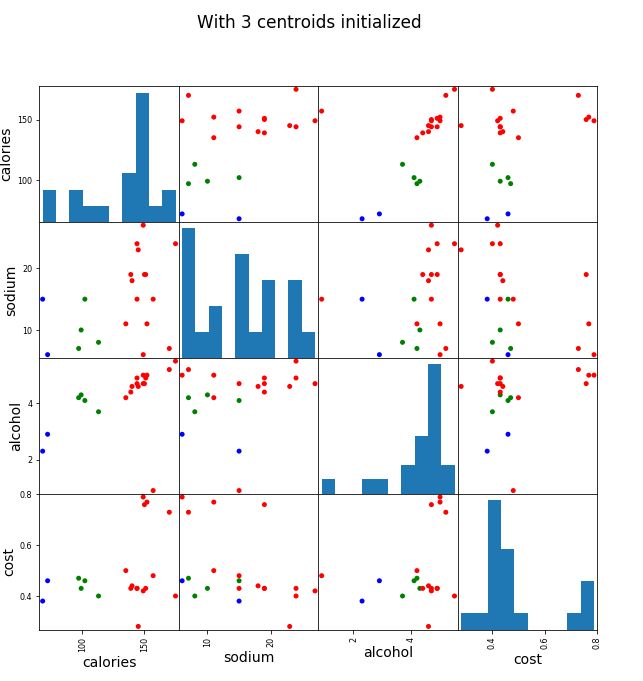
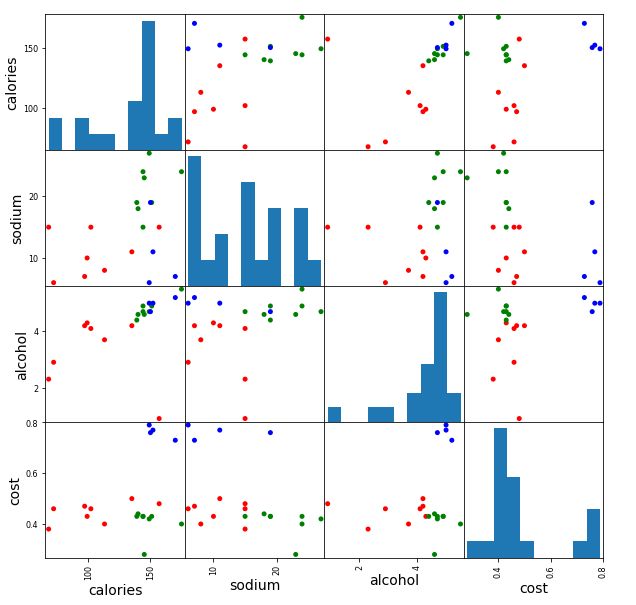
簇数为3的散点矩阵图

scatter_matrix(beer[["calories","sodium","alcohol","cost"]],
			   s=100,c=colors[beer['cluster']],figsize=(10,10))
plt.suptitle("With 3 centroids initialized")

簇数为2的散点矩阵图

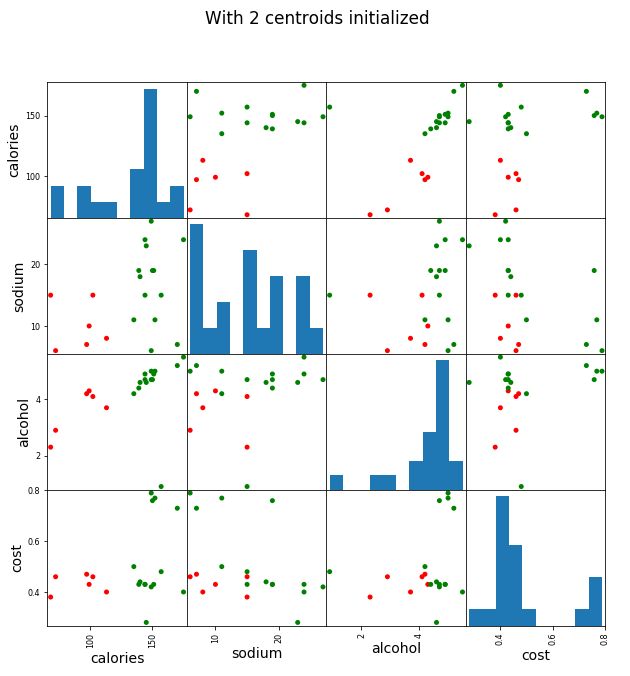
scatter_matrix(beer[["calories","sodium","alcohol","cost"]],
			   s=100,alpha=1,c=colors[beer['cluster2']],figsize=(10,10))
plt.suptitle('With 2 centroids initialized')

2.2标准化数据集之后的结果

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
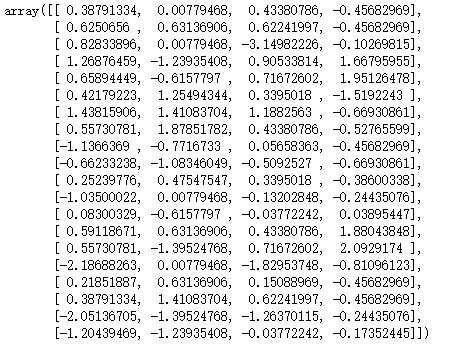
X_scaled = scaler.fit_transform(X)
X_scaled

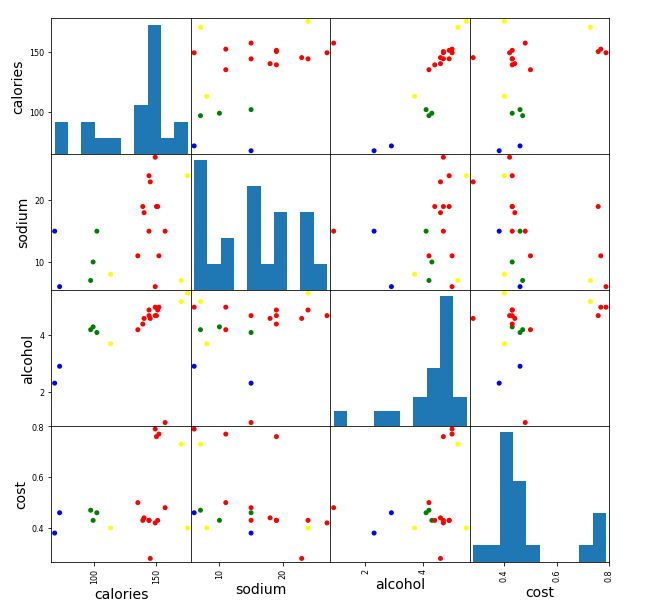
km = KMeans(n_clusters=3).fit(X_scaled)
beer["scaled_cluster"] = km.labels_

scatter_matrix(X,s=100,c=colors[beer['scaled_cluster']],alpha=1,figsize=(10,10))

      聚类评估：轮廓系数（Silhouette Coefficient ）

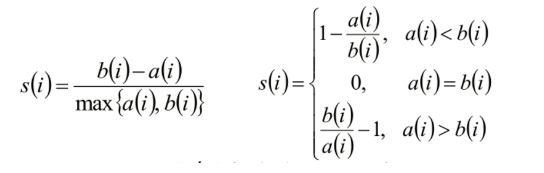
• 计算样本i到同簇其他样本的平均距离ai。ai 越小，说明样本i越应该被聚类到该簇。将ai 称为样本i的簇内不相似度。
• 计算样本i到其他某簇Cj 的所有样本的平均距离bij，称为样本i与簇Cj 的不相似度。定义为样本i的簇间不相似度：bi =min{bi1, bi2, …, bik}
• si接近1，则说明样本i聚类合理
• si接近-1，则说明样本i更应该分类到另外的簇
• 若si 近似为0，则说明样本i在两个簇的边界上。

比较标准化数据和为标准化数据的聚类效果

from sklearn import metrics
score_scaled = metrics.silhouette_score(X,beer.scaled_cluster)
score = metrics.silhouette_score(X,beer.cluster)
print(score_scaled,score)

输出结果：0.1797806808940007      0.6731775046455796
      注：怎么回事？标准化之后的数据，进行聚类，效果反而比未进行标准化的差？这说明一个问题：数据集的一些特征本身就是非常重要的，就需要把它放大，但是呢，由于我们的标准化使得它的特征不那么明显了，从而影响到了聚类效果。
2.3通过设置不同的簇的数量，观察聚类效果

scores = []
for k in range(2,20):
    labels = KMeans(n_clusters=k).fit(X).labels_
    score = metrics.silhouette_score(X,labels)
    scores.append(score)

plt.plot(list(range(2,20)), scores)
plt.xlabel("Number of Clusters Initialized")
plt.ylabel("Sihouette Score")

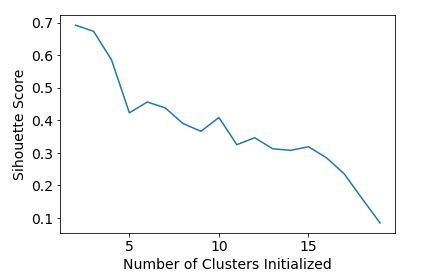
      注：可以发现，最好的簇的数量就是2。
3.DBSCAN聚类算法

from sklearn.cluster import DBSCAN
db = DBSCAN(eps=10,min_samples=2).fit(X)

labels = db.labels_
beer['cluster_db'] = labels
scatter_matrix(X,s=100,c=colors[beer['cluster_db']],alpha=1,figsize=(10,10))

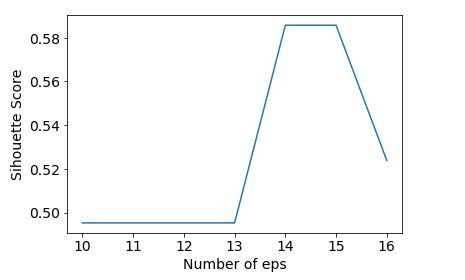
scores = []
for r,k in [(10,2), (11,2), (12,2), (13,2), (14,2), (15,2), (16,2)]:
    labels = DBSCAN(eps=r,min_samples=k).fit(X).labels_
    score = metrics.silhouette_score(X,labels)
scores.append(score)

plt.plot(range(10,17),scores)
plt.xlabel('Number of eps')
plt.ylabel('Sihouette Score')

scores = []
for r,k in [(14,2), (14,3), (14,4), (14,5), (14,6)]:
    labels = DBSCAN(eps=r,min_samples=k).fit(X).labels_
    score = metrics.silhouette_score(X,labels)
    scores.append(score)

plt.plot(range(2,7),scores)
plt.xlabel('Number of min_samples')
plt.ylabel('Sihouette Score')

参考文档：
https://blog.csdn.net/wangxingfan316/article/details/80033557