线性方程组应用举例

线性方程组应用举例

今天我们要说的就是线性方程组应用举例，本文是《科学计算与MATLAB语言》专题六第3小节的学习笔记，如果大家有时间的话，可以去听听课，没有的话，可以看看我的笔记，还是很不错的。

1 平面桁架结构受力分析问题

桁架是工程中常用的一种结构，各构件在同一平面内的桁架称为平面桁架。一个平面桁架结构由连接于A、B、C、D、E、F、G、H共8个结点的13根杆件构成。在结点B、E和G上施加指定载荷，求桁架每根杆件上的轴力。

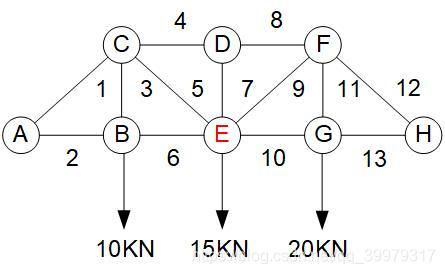
对于静态平衡的衍架而言，它的各个结点也一定是平衡的，即在任何结点上水平方向或垂直方向受力之和都必须为零。因此，可以对每一个结点列出两个独立的平衡方程，从而可求出杆件的轴力。对于8个结点，可以列出16个方程，方程数多于待定的13个未知量。为使该衍架静定，即为使问题存在唯一解，我们假定：
1.结点A在水平和垂直方向上刚性固定
2.结点H仅在垂直方向刚性固定。
以结点E为例，其受力如图所示。

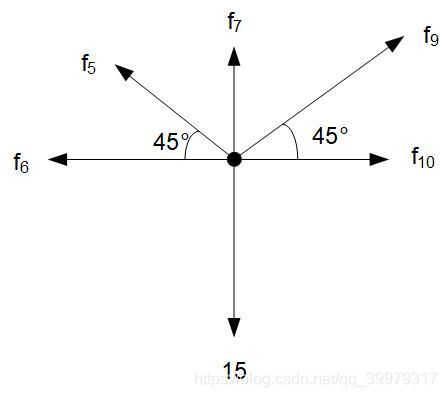
写出平衡方程，有：
水平方向：
$$f_{5}cos45°+f_6=f_{9}cos45°+f_{10}$$
垂直方向：
$$f_{5}sin45°+f_7+f_{9}sin45°=15$$
定义参数$a=\sqrt{2}/2$，
则可得到E点的平衡方程。
$$\{\begin{array}{rl}a{f}_5+f_6& =a{f}_9+f_{10}\\ a{f}_5+f_7+a{f}_9& =15\end{array}$$
结点B:
$$\{\begin{array}{r}{f}_2=f_6\\ f_3=10\end{array}$$
结点C:
$$\{\begin{array}{rl}a{f}_1& =f_4+a{f}_5\\ a{f}_1+f_3+a{f}_5& =0\end{array}$$
结点D:
$$\{\begin{array}{rl}{f}_4& =f_8\\ f_7& =0\end{array}$$
结点E:
$$\{\begin{array}{rl}a{f}_5+f_6& =a{f}_9+f_{10}\\ a{f}_5+f_7+a{f}_9& =15\end{array}$$
结点F:
$$\{\begin{array}{rl}{f}_{10}& =f_{13}\\ f_{11}& =20\end{array}$$
结点G:
$$\{\begin{array}{rl}{f}_8+a{f}_9& =a{f}_{12}\\ a{f}_9+f_{11}+a{f}_{12}& =0\end{array}$$
结点H:
$$f_{13}+a{f}_{12}=0$$
结点H在垂直方向刚性固定，只有水平方向平衡方程。
这是一个包含13个未知数的线性方程组，利用MATLAB很容易求出杆件轴力向量f。

alpha=sqrt(2)/2; 
A=[0,1,0,0,0,-1,0,0,0,0,0,0,0;
0,0,1,0,0,0,0,0,0,0,0,0,0;
alpha,0,0,-1,-alpha,0,0,0,0,0,0,0,0; 
alpha,0,1,0,alpha,0,0,0,0,0,0,0,0;
0,0,0,1,0,0,0,-1,0,0,0,0,0;
0,0,0,0,0,0,1,0,0,0,0,0,0;
0,0,0,0,alpha,1,0,0,-alpha,-1,0,0,0;
0,0,0,0,alpha,0,1,0,alpha,0,0,0,0;
0,0,0,0,0,0,0,0,0,1,0,0,-1;
0,0,0,0,0,0,0,0,0,0,1,0,0;
0,0,0,0,0,0,0,1,alpha,0,0,-alpha,0;
0,0,0,0,0,0,0,0,alpha,0,1,alpha,0;
0,0,0,0,0,0,0,0,0,0,0,alpha,1]; 
b=[0;10;0;0;0;0;0;15;0;20;0;0;0]; 
f=A\b; 
disp(f')

 -28.2843   20.0000   10.0000  -30.0000   14.1421   20.0000         0  -30.0000    7.0711   25.0000   20.0000  -35.3553   25.0000

桁架杆件主要承受轴向拉力或压力，当杆件受拉时，轴力为拉力，其指向背离截面；当杆件受压时，轴力为压力，其指向指向截面。答案中的正数表示拉力，负数表示压力。

2 小行星运行轨道计算问题

现在已经在5个不同时刻对某颗小行星进行了5次观测，测得轨道上的5个点的坐标数据如表所示，其单位为天文测量单位。试确定小行星的轨道方程。

i	1	2	3	4	5
$$x_i$$	1.02	0.87	0.67	0.44	0.16
$$y_i$$	0.39	0.27	0.18	0.13	0.13

（1）模型分析
由开普勒第一定律知，小行星运行轨道为椭圆方程：
$$a_1{x}^2+2a_{2}xy+a_3{y}^2+2a_{4}x+2a_{5}y+1=0$$
需要确定系数$a_i（i=1，2，3，4，5）。$
利用已知的数据，不妨设测得的5个点坐标为$（x_i，y_i）（i=1，2，3，4，5），$确定系数$a_i$等价于求解下列线性方程组。
$$\{\begin{array}{r}{a}_1{x}_1^2+2a_2{x}_1{y}_1+a_3{y}_1^2+2a_4{x}_1+2a_5{y}_1+1=0\\ a_1{x}_2^2+2a_2{x}_2{y}_1+a_3{y}_2^2+2a_4{x}_2+2a_5{y}_2+1=0\\ a_1{x}_3^2+2a_2{x}_3{y}_1+a_3{y}_3^2+2a_4{x}_3+2a_5{y}_3+1=0\\ a_1{x}_4^2+2a_2{x}_4{y}_1+a_3{y}_4^2+2a_4{x}_4+2a_5{y}_4+1=0\\ a_1{x}_5^2+2a_2{x}_5{y}_1+a_3{y}_5^2+2a_4{x}_5+2a_5{y}_5+1=0\end{array}$$
将方程改写为：

xi=[1.02,0.87,0.67,0.44,0.16]; 
yi=[0.39,0.27,0.18,0.13,0.13]; 
A=zeros(length(xi)); 
for i=1: length(xi)
A(i,:)=[ xi(i)* xi(i),2* xi(i)* yi(i), yi(i)* yi(i),2* xi(i),2* yi(i)]; 
end
b=-ones(length(xi),1);
ai=A\b

ai =

    2.4645
   -0.4423
    6.4917
   -0.6819
   -3.6008

因此小行星的轨道方程为：
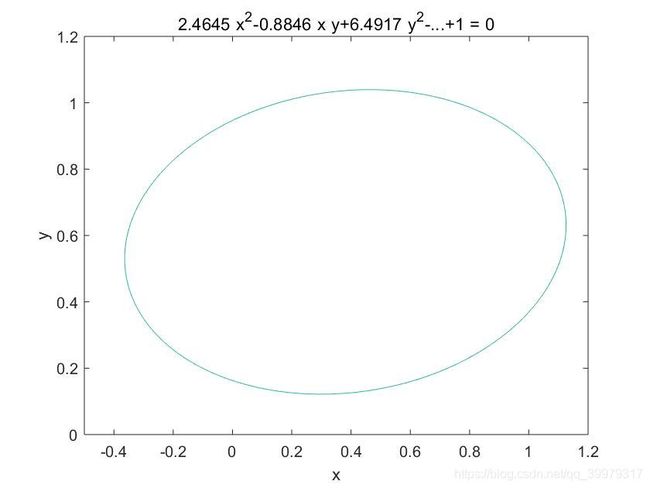
$$2.4645x^2-0.8846xy+6.4917y^2-1.3638x-7.2016y+1=0$$
绘制小行星运行轨道：

f=@(x,y) 2.4645*x.^2-0.8846*x.*y+6.4917*y.^2-1.3638*x-7.2016*y+1;
h=ezplot(f,[-0.5,1.2,0,1.2]);

欢迎大家
点赞，收藏⭐，转发，
如有问题、建议，请您在评论区留言哦。