MATLAB实现中频正交采样（数字下变频）

数字下变频原理

  在数字信号处理中获得零中频数字信号的办法是将中频信号通过抗混叠滤波器，得到

再经过同相支路乘法器（乘法信号由相参振荡器获得，是一个中频正弦波）得到同相分量

将上述信号通过低通滤波器就得到同相分量

同理可得正交支路输出信号为

低通滤波后得到正交分量

对数字信号也是如此，对模拟信号数字采样，得到

对其进行混频，过低通滤波，得到$x_I(n)=a(n)\cos {\varphi }_n$和$x_Q(n)=a(n)sin{\varphi }_n$。当采样频率为$f_s=\frac{4f_{IF}}{2m-1}$时，有

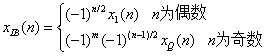
  贝塞尔插值法也是基于莱斯变换的数字下变频方法，直接中频采样输出$x(n)$经过符号修正和奇偶分离后，未得到同一时刻的同相分量和正交分量，最直接的方式就是进行插值，常用方法是贝塞尔插值。贝塞尔插值使用一个多项式函数来逼近一个带限函数。其中点插值公式为

代码实现

%% IIR低通滤波器的设计
clc;
close all;
clear all;
 
Fs = 100000; % 采样频率
T = 0.01; % 信号持续时间
t = 0:1/Fs:(T-1/Fs); %采样点
n = length(t); % 采样点数
 
% 测试信号
y = cos(2*pi*10000*t)+2*cos(2*pi*20000*t)+0.1*randn(size(t));
figure(1);
plot(t,y);grid on;
 
% 频域变换
J = fft(y,n); 
% 若做N点fft，则得到的序列长度为N，为将其显示为真实频率，需要取一半序列长度,(0:N/2-1)
% 除以N，再乘以时域采样频率Fs
% 在上面的程序中，因为是n点fft，所以在下面不需要除以N乘以Fs，而是直接取一半的点
 
f_fft = (1:n/2)/n*Fs; % 取频谱一半
J = J./n*2; % 幅度归一化
J_amplitude = abs(J); % 幅频响应曲线
 
figure(2)
plot(f_fft,J_amplitude(1:n/2)); % 图中的峰 单位Hz
xlabel('Hz');ylabel('幅值'); 
title('原始信号频谱');
grid on;
 
% IIR滤波器设计
N=0; % 阶数
Fp=11000; % 通带截止频率11KHz
Fc=20000; % 阻带截止频率20KHz，意为高于此频率的信号要满足至少60dB的衰减
Rp=1; % 通带波纹最大衰减为1dB
Rs=60; % 阻带衰减为60dB
 
% 计算最小滤波器阶数
na=sqrt(10^(0.1*Rp)-1);
ea=sqrt(10^(0.1*Rs)-1);
N=ceil(log10(ea/na)/log10(Fc/Fp));
 
% 巴特沃斯滤波器
Wn=Fp*2/Fs;  
[Bb,Ba]=butter(N,Wn,'low'); % 调用MATLAB butter函数快速设计滤波器  
[BH,BW]=freqz(Bb,Ba); % 绘制频率响应曲线  
Bf=filter(Bb,Ba,y); % 进行低通滤波  
By=fft(Bf,n);  % 对滤波后信号做n点FFT变换  
 
figure(3);
plot(t,y,'blue',t,Bf,'red');grid;
legend('10KHz,20KHz带噪原始信号','巴特沃斯低通滤波后信号');  
 
figure(4);
plot(f_fft,abs(By(1:n/2)./n*2));grid;  
title('巴特沃斯低通滤波后信号频谱');  
xlabel('Hz');ylabel('幅值'); 
 
Hf = 20*log10(abs(BH));
Hx = angle(BH);
plot(BW/pi*Fs,Hf);grid on;
axis([0 80000 -100 20]);
title('巴特沃斯低通滤波器幅频响应曲线');
%% FIR低通滤波器的设计
% 通带截止频率ωp→理想低通滤波器的截止频率ωd
clear all;
close all;
clc;
wd = 0.2*pi; % 截止频率
N = 101; % 窗长度，一般奇数
M = (N-1)/2;
nn = -M:M;
n = nn+eps; % eps是很小的正常数
hd = sin(wd*n)./(pi*n); % 理想低通滤波器的时域形式，若n趋于无穷
w1 = boxcar(N)';h1 = hd.*w1; % 矩形窗
w2 = hanning(N)';h2 = hd.*w2; % 汉宁窗
w3 = hamming(N)';h3 = hd.*w3; % 哈明窗
w4 = blackman(N)';h4 = hd.*w4; % 布莱克曼窗
H1 = 20*log10(abs(fft(h1,4096)));
H2 = 20*log10(abs(fft(h2,4096)));
H3 = 20*log10(abs(fft(h3,4096)));
H4 = 20*log10(abs(fft(h4,4096)));
% HH1 = [H1(513:1024),H1(1:512)];
% HH2 = [H2(513:1024),H2(1:512)];
% HH3 = [H3(513:1024),H3(1:512)];
% HH4 = [H4(513:1024),H4(1:512)];
HH1 = fftshift(H1);
HH2 = fftshift(H2);
HH3 = fftshift(H3);
HH4 = fftshift(H4);
w = (-2048:2047)/2048;
figure(1);
plot(w,HH1,w,HH2,':',w,HH3,'-',w,HH4,'--');grid on;
axis([-1.1 1.1 -150 20]);
legend('矩形','汉宁','哈明','布莱克曼');
xlabel('\omega/\pi');
set(gcf,'color','w');
 
% 测试信号
Fs = 100000; % 采样频率
T = 0.01; % 信号持续时间
t = 0:1/Fs:(T-1/Fs); %采样点
n = length(t); % 采样点数
 
y = cos(2*pi*10000*t)+2*cos(2*pi*20000*t)+0.1*randn(size(t));
figure(2);
plot(t,y);grid on;
 
% 频域变换
J = fft(y,n); 
f_fft = (1:n/2)/n*Fs; % 取频谱一半
J = J./n*2; % 幅度归一化
 
figure(3);
plot(f_fft,abs(J(1:n/2))); grid on;% 幅频响应曲线 单位Hz
xlabel('f/Hz');ylabel('magnitude'); 
title('原始信号频谱');
 
% 低通滤波 
y_filtered = conv(y,h4);
 
% 频域变换
J_filtered = fft(y_filtered(floor(length(h1)/2):length(y_filtered)-length(h1)/2),n); 
J_filtered = J_filtered./n*2; % 幅度归一化
 
figure(5);
plot(f_fft,abs(J_filtered(1:n/2))); grid on;% 幅频响应曲线 单位Hz
xlabel('f/Hz');ylabel('magnitude'); 
title('滤波后信号频谱');
%% 单频信号的正交相位检波（数字下变频）
 
clc;
close all;
clear all;
 
Fs = 100000; % 采样频率
T = 0.01; % 信号持续时间
t = 0:1/Fs:(T-1/Fs); %采样点
n = length(t); % 采样点数
 
% 中频输入信号 x_IF(t)=a(t)cos[2π*f_IF*t+φ(t)]+n(t)
% 经过带通滤波器得到x_IB(t)≈x_IF(t)
f_IF = 10000; % 中频10KHz
x_IB = cos(2*pi*f_IF*t+0.3*pi)+0.1*randn(size(t));
figure(1);
plot(t,x_IB);grid on;
 
% 相参振荡信号 2cos(2π*f_IF*t)和-2sin(2π*f_IF*t)
x1 = 2*cos(2*pi*f_IF*t);
x2 = -2*sin(2*pi*f_IF*t);
 
% 中频信号与相参振荡信号相乘
y1 = x_IB.* x1; % 同相支路
y2 = x_IB.* x2; % 正交支路
 
% 构造巴特沃斯低通滤波器
N=0; % 阶数
Fp=1.1*f_IF; % 通带截止频率11KHz
Fc=2*f_IF; % 阻带截止频率20KHz，意为高于此频率的信号要满足至少60dB的衰减
Rp=1; % 通带波纹最大衰减为1dB
Rs=60; % 阻带衰减为60dB
 
% 计算最小滤波器阶数
na=sqrt(10^(0.1*Rp)-1);
ea=sqrt(10^(0.1*Rs)-1);
N=ceil(log10(ea/na)/log10(Fc/Fp));
 
% 巴特沃斯滤波器
Wn=Fp*2/Fs;  
[Bb,Ba]=butter(N,Wn,'low'); % 调用MATLAB butter函数快速设计滤波器  
[BH,BW]=freqz(Bb,Ba); % 求离散系统频率响应
 
% 过低通滤波器
x_I = filter(Bb,Ba,y1);   
x_Q = filter(Bb,Ba,y2);
 
% By=fft(Bf,n);  % 对滤波后信号做n点FFT变换
%% LFM信号的正交相位检波（数字下变频）
clc;
close all;
clear all;
 
Fs = 100000; % 采样频率
T = 0.01; % 信号持续时间
t = 0:1/Fs:(T-1/Fs); %采样点
n = length(t); % 采样点数
 
% 中频输入信号 x_IF(t)=a(t)cos[2πf0 t+πkt^2]+n(t)
% a(t)是包络，f0是调频频率
% 经过带通滤波器得到x_IB(t)≈x_IF(t)
A_lfm = 1;
f_lfm = 10000;
k_lfm = 800000;
x_IB = A_lfm*( cos(2*pi*f_lfm*t + pi*k_lfm*t.^2) + 0.1*randn(size(t)) );
figure(1);
plot(t(1:500),x_IB(1:500));grid on;
xlabel('t/s');
title('线性调频信号波形');
axis([0 0.005 -A_lfm A_lfm]);
 
% 相参振荡信号 2cos(2π*f_IF*t)和-2sin(2π*f_IF*t)
x1 = 2*cos(2*pi*f_lfm*t);
x2 = -2*sin(2*pi*f_lfm*t);
 
% 中频信号与相参振荡信号相乘
y1 = x_IB.* x1; % 同相支路
y2 = x_IB.* x2; % 正交支路
 
% 构造巴特沃斯低通滤波器
N=0; % 阶数
Fp=1.1*f_lfm; % 通带截止频率11KHz
Fc=2*f_lfm; % 阻带截止频率20KHz，意为高于此频率的信号要满足至少60dB的衰减
Rp=1; % 通带波纹最大衰减为1dB
Rs=60; % 阻带衰减为60dB
 
% 计算最小滤波器阶数
na=sqrt(10^(0.1*Rp)-1);
ea=sqrt(10^(0.1*Rs)-1);
N=ceil(log10(ea/na)/log10(Fc/Fp));
 
% 巴特沃斯滤波器
Wn=Fp*2/Fs;  
[Bb,Ba]=butter(N,Wn,'low'); % 调用MATLAB butter函数快速设计滤波器  
[BH,BW]=freqz(Bb,Ba); % 求离散系统频率响应
 
% 过低通滤波器
x_I = filter(Bb,Ba,y1); % 同相分量 
x_Q = filter(Bb,Ba,y2); % 正交分量
 
figure(2);
plot(x_I);
figure(3);
plot(x_Q);
 
% 对滤波后信号做n点FFT变换
X_I = fft(x_I,n); 
f_fft = (1:n/2)/n*Fs; % 取频谱一半
X_I = X_I./n*2; % 幅度归一化
X_I_amplitude = abs(X_I); % 幅频响应曲线
figure(4);
plot(f_fft,X_I_amplitude(1:n/2)); % 图中的峰 单位Hz
xlabel('Hz');ylabel('幅值'); grid on;
title('同相信号频谱');
 
X_Q = fft(x_Q,n); 
X_Q = X_Q./n*2; % 幅度归一化
figure(5);
plot(f_fft,abs(X_Q(1:n/2))); % 幅频响应曲线 单位Hz
xlabel('Hz');ylabel('幅值'); grid on;
title('正交信号频谱');
 
x_IB = fft(x_IB,n); 
x_IB = x_IB./n*2; % 幅度归一化
figure(6);
plot(f_fft,abs(x_IB(1:n/2))); % 幅频响应曲线 单位Hz
xlabel('Hz');ylabel('幅值'); grid on;
title('原信号频谱');
%% BPSK信号的正交相位检波（数字下变频）
clc;
close all;
clear all;
 
Fs = 100000; % 采样频率
T = 0.01; % 信号持续时间
t = 0:1/Fs:(T-1/Fs); %采样点
n = length(t); % 采样点数
 
% 中频输入信号 x_IF(t) = BPSK信号
binary_code = '1001100110';
len_code = length(binary_code); % bit串对应的脉冲个数
f_bpsk = 1000; % 频率1000Hz，周期1ms
T_bpsk = 1/f_bpsk;
A_bpsk = 10; % 幅值
t_mayuan = 0:1/Fs:(2*T_bpsk-1/Fs); % 一个码元所持续的时间内的采样点时刻
y_mayuan = A_bpsk*sin(2*pi*f_bpsk*t_mayuan); % 一个码元的波形，用于表示0
t_bpsk = 0:1/Fs:(2*T_bpsk*len_code-1/Fs);
x_IB = []; % 产生BPSK波形
for i=1:len_code
    tmp = str2num(binary_code(i));
    if tmp == 0
        x_IB = [x_IB,y_mayuan];
    end
    if tmp == 1
        x_IB = [x_IB,-y_mayuan];
    end
end
figure(1); % 画原信号波形
plot(t_bpsk,x_IB);grid on;
xlabel('t/s');title('‘1001100110’的BPSK编码信号');
axis([0 2e-2 -2*A_bpsk 2*A_bpsk]);
 
% 相参振荡信号 2cos(2π*f_IF*t)和-2sin(2π*f_IF*t)
x1 = 2*cos(2*pi*f_bpsk*t_mayuan);
x2 = -2*sin(2*pi*f_bpsk*t_mayuan);
 
% 构造巴特沃斯低通滤波器
N=0; % 阶数
Fp=1*f_bpsk; % 通带截止频率11KHz
Fc=3*f_bpsk; % 阻带截止频率20KHz，意为高于此频率的信号要满足至少60dB的衰减
Rp=1; % 通带波纹最大衰减为1dB
Rs=60; % 阻带衰减为60dB
 
na=sqrt(10^(0.1*Rp)-1); % 计算最小滤波器阶数
ea=sqrt(10^(0.1*Rs)-1);
N=ceil(log10(ea/na)/log10(Fc/Fp));
 
Wn=Fp*2/Fs;  
[Bb,Ba]=butter(N,Wn,'low'); % 调用MATLAB butter函数快速设计滤波器  
[BH,BW]=freqz(Bb,Ba); % 求离散系统频率响应
 
xi = [];
xq = [];
yi = [];
yq = [];
for i =1:10
% 中频信号与相参振荡信号相乘
y1 = x_IB( (i-1)*200+1:i*200 ).* x1; % 同相支路
y2 = x_IB( (i-1)*200+1:i*200 ).* x2; % 正交支路
 
yi = [yi,y1];
yq = [yq,y2];
% 过低通滤波器
x_I = filter(Bb,Ba,y1);   
x_Q = filter(Bb,Ba,y2);
xi = [xi,x_I];
xq = [xq,x_Q];
% By=fft(Bf,n);  % 对滤波后信号做n点FFT变换
end
y_Q = filter(Bb,Ba,yq);
y_I = filter(Bb,Ba,yi);
figure(2);
plot(yi,'b');hold on;
% figure(3);
plot(y_I,'r')
 
figure(3);
plot(yq,'b');hold on;
% figure(3);
plot(y_Q,'r')
 
figure(4);
plot(yi,'b');hold on;
% figure(3);
plot(xi,'r')
%% 单频信号的数字下变频的贝塞尔插值法
clc;
close all;
clear all;
 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 此处是用离散点来模拟连续时间的，在本质上还是变量t
% f表示t变化的步长，值越小越能够模拟连续时间信号
f = 100000; % 采样频率
T = 0.1; % 信号持续时间
t = 0:1/f:(T-1/f); %采样点
n = length(t); % 采样点数
f_IF = 10000; % 中频10KHz
% 模拟中频信号
x_IB = cos(2*pi*f_IF*t+0.3*pi)+0.1*randn(size(t));
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
% 频域变换
J = fft(x_IB,n); f_fft = (1:n/2)/n*f; % 取频谱一半
J = J./n*2; % 幅度归一化
figure(1);
plot(f_fft,abs(J(1:n/2))); grid on;% 幅频响应曲线 单位Hz
xlabel('f/Hz');ylabel('magnitude'); 
title('原始信号频谱');
 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 对x_IB(t)进行等间隔采样，采样周期Ts，频率Fs
% Fs须满足中频采样定理，最佳采样频率为 4*f_IF/(2*m-1)
% 1≤m≤floor(f_u/B),f_u是信号最高频率，B是带宽=f_u-f_l
% 从原始信号频谱图中读出带宽为200Hz，f_u取f_IF
B = 200; % 信号带宽200Hz
m_max = floor(f_IF/B);
m = 1;
Fs = 4*f_IF/(2*m-1);
% 即t=n*Ts，AD变换前后应保证时域长度一致
% 即n_max=t_max/Ts
% 数字采样后的中频信号x_IB(n)=cos[2πf_IF*Ts*n+φ(nTs)]+n(t)
 
nn = 0:max(t)*Fs;
phi = 0.3*pi;
x_IB = cos(2*pi*f_IF/Fs*nn+phi)+0.1*randn(size(nn));
figure(2);
plot(nn(1:200),x_IB(1:200));grid on;
axis([1 200 -1.5 1.5]);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
x_I = zeros(1,length(nn));
x_Q = zeros(1,length(nn));
for i =1:length(nn)
    if mod(nn(i),2) == 0
        x_I(i) = x_IB(i)/( (-1)^(nn(i)/2) ); 
    end
    if mod(nn(i),2) == 1
        x_Q(i) = x_IB(i)/( (-1)^m*(-1)^((nn(i)-1)/2) );
    end
end
% 4阶贝塞尔插值
for i=1:2000
    
    if i == 1 || i == 1999
        x_I(2*i) = 0.5*(x_I(2*i-1) + x_I(2*i+1));
    end
    if i == 2000
        x_I(2*i) = x_I(2*i-1);
    end  
    if i ~= 1 && i ~= 1999 && i ~= 2000
        x_I(2*i) = (9*x_I(2*i-1)+9*x_I(2*i+1)-x_I(2*i-3)-x_I(2*i+3))/16;
    end
end
for i=1:2000
    if i == 1
        x_Q(2*i-1) = x_Q(2*i);
    end
    if i == 2 || i == 2000
        x_Q(2*i-1) = 0.5*(x_Q(2*i-2) + x_Q(2*i));
    end
    if i ~= 1 && i ~= 2 && i ~= 2000
        x_Q(2*i-1) = (9*x_Q(2*i-2)+9*x_Q(2*i)-x_Q(2*i-4)-x_Q(2*i+2))/16;
    end
end
figure(3);
plot(nn,x_Q,nn,sin(phi)*ones(1,length(nn)));grid on;title('正交支路信号');
figure(4);
plot(nn,x_I,nn,cos(phi)*ones(1,length(nn)));grid on;title('同相支路信号');
%% LFM信号的数字下变频的贝塞尔插值法
clc;
close all;
clear all;
 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 此处是用离散点来模拟连续时间的，在本质上还是变量t
% f表示t变化的步长，值越小越能够模拟连续时间信号
f = 100000; % 采样频率
T = 0.1; % 信号持续时间
t = 0:1/f:(T-1/f); %采样点
n = length(t); % 采样点数
A_lfm = 1; % 信号包络
f_lfm = 10000; % 初始频率
k_lfm = 800000; % 频率变化率
% 模拟中频信号 x_IF(t)=a(t)cos[2πf0 t+πkt^2]+n(t)
x_IB = A_lfm*( cos(2*pi*f_lfm*t + pi*k_lfm*t.^2) + 0.1*randn(size(t)) );
figure(1);
plot(t(1:500),x_IB(1:500));grid on;
xlabel('t/s');ylabel('幅度');
title('线性调频信号波形');
axis([0 0.005 -A_lfm A_lfm]);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
% 频域变换
J = fft(x_IB,n); f_fft = (1:n/2)/n*f; % 取频谱一半
J = J./n*2; % 幅度归一化
figure(2);
plot(f_fft,abs(J(1:n/2))); grid on;% 幅频响应曲线 单位Hz
xlabel('f/Hz');ylabel('magnitude'); 
title('原始信号频谱');
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 对x_IB(t)进行等间隔采样，采样周期Ts，频率Fs
% Fs须满足中频采样定理，最佳采样频率为 4*f_IF/(2*m-1)
% 1≤m≤floor(f_u/B),f_u是信号最高频率，B是带宽=f_u-f_l
% 从原始信号频谱图中读出带宽为200Hz，f_u取f_IF
B = 40000; % 信号带宽200Hz
m_max = floor(f_lfm/B);
m = 1;
Fs = 4*f_lfm/(2*m-1);
% 即t=n*Ts，AD变换前后应保证时域长度一致
% 即n_max=t_max/Ts
% 数字采样后的中频信号x_IB(n)=cos[2πf_IF*Ts*n+φ(nTs)]+n(t)
% x_IF(t)=a(t)cos[2πf0 t+πkt^2]+n(t)
nn = 0:max(t)*Fs;
% phi = 0.3*pi;
x_IB1 = A_lfm*(cos(2*pi*f_lfm/Fs*nn+pi*k_lfm*(nn/Fs).*(nn/Fs))+0.1*randn(size(nn)));
figure(3);
plot(nn(1:200),x_IB1(1:200));grid on;
axis([1 200 -1.5 1.5]);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
x_I = zeros(1,length(nn));
x_Q = zeros(1,length(nn));
for i =1:length(nn)
    if mod(nn(i),2) == 0
        x_I(i) = x_IB(i)/( (-1)^(nn(i)/2) ); 
    end
    if mod(nn(i),2) == 1
        x_Q(i) = x_IB(i)/( (-1)^m*(-1)^((nn(i)-1)/2) );
    end
end
 
% 4阶贝塞尔插值
for i=1:2000
    
    if i == 1 || i == 1999
        x_I(2*i) = 0.5*(x_I(2*i-1) + x_I(2*i+1));
    end
    if i == 2000
        x_I(2*i) = x_I(2*i-1);
    end  
    if i ~= 1 && i ~= 1999 && i ~= 2000
        x_I(2*i) = (9*x_I(2*i-1)+9*x_I(2*i+1)-x_I(2*i-3)-x_I(2*i+3))/16;
    end
end
for i=1:2000
    if i == 1
        x_Q(2*i-1) = x_Q(2*i);
    end
    if i == 2 || i == 2000
        x_Q(2*i-1) = 0.5*(x_Q(2*i-2) + x_Q(2*i));
    end
    if i ~= 1 && i ~= 2 && i ~= 2000
        x_Q(2*i-1) = (9*x_Q(2*i-2)+9*x_Q(2*i)-x_Q(2*i-4)-x_Q(2*i+2))/16;
    end
end
figure(3);
plot(nn,x_Q);grid on;title('正交支路信号');
figure(4);
plot(nn,x_I);grid on;title('同相支路信号');
%% BPSK信号的数字下变频的贝塞尔插值法
clc;
close all;
clear all;
 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 此处是用离散点来模拟连续时间的，在本质上还是变量t
% f表示t变化的步长，值越小越能够模拟连续时间信号
f = 100000; % 采样频率
T = 0.1; % 信号持续时间
t = 0:1/f:(T-1/f); %采样点
n = length(t); % 采样点数
% 中频输入信号 x_IF(t) = BPSK信号
binary_code = '1001100110';
len_code = length(binary_code); % bit串对应的脉冲个数
f_bpsk = 1000; % 频率1000Hz，周期1ms
T_bpsk = 1/f_bpsk;
A_bpsk = 10; % 幅值
t_mayuan = 0:1/f:(20*T_bpsk-1/f); % 一个码元所持续的时间内的采样点时刻
y_mayuan = A_bpsk*sin(2*pi*f_bpsk*t_mayuan); % 一个码元的波形，用于表示0
t_bpsk = 0:1/f:(20*T_bpsk*len_code-1/f);
x_IB = []; % 产生BPSK波形
for i=1:len_code
    tmp = str2num(binary_code(i));
    if tmp == 0
        x_IB = [x_IB,y_mayuan];
    end
    if tmp == 1
        x_IB = [x_IB,-y_mayuan];
    end
end
figure(1); % 画原信号波形
plot(t_bpsk,x_IB);grid on;
xlabel('t/s');title('‘1001100110’的BPSK编码信号');
axis([0 2e-1 -2*A_bpsk 2*A_bpsk]);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
% 频域变换
J = fft(x_IB,n); f_fft = (1:n/2)/n*f; % 取频谱一半
J = J./n*2; % 幅度归一化
figure(2);
plot(f_fft,abs(J(1:n/2))); grid on;% 幅频响应曲线 单位Hz
xlabel('f/Hz');ylabel('magnitude'); 
title('原始信号频谱');
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 对x_IB(t)进行等间隔采样，采样周期Ts，频率Fs
m = 1;
Fs = 4*f_bpsk/(2*m-1);
% 即t=n*Ts，AD变换前后应保证时域长度一致
% 即n_max=t_max/Ts
nn = 0:max(t_mayuan)*Fs;
 
y_my = A_bpsk*sin(2*pi*f_bpsk*nn/Fs); % 一个码元的波形，用于表示0
n_bpsk = 0:length(nn)*len_code-1;
x_IB1 = []; % 产生BPSK波形
for i=1:len_code
    if str2num(binary_code(i)) == 0
        x_IB1 = [x_IB1,y_my];
    end
    if str2num(binary_code(i)) == 1
        x_IB1 = [x_IB1,-y_my];
    end
end
 
figure(3);
plot(n_bpsk,x_IB1);grid on;
axis([1 length(x_IB1) -2*A_bpsk 2*A_bpsk]);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
x_I = zeros(1,length(n_bpsk));
x_Q = zeros(1,length(n_bpsk));
for i =1:length(n_bpsk)
    if mod(n_bpsk(i),2) == 0
        x_I(i) = x_IB(i)/( (-1)^(n_bpsk(i)/2) ); 
    end
    if mod(n_bpsk(i),2) == 1
        x_Q(i) = x_IB(i)/( (-1)^m*(-1)^((n_bpsk(i)-1)/2) );
    end
end
%
% 4阶贝塞尔插值
for i=1:400
    
    if i == 1 || i == 399
        x_I(2*i) = 0.5*(x_I(2*i-1) + x_I(2*i+1));
    end
    if i == 400
        x_I(2*i) = x_I(2*i-1);
    end  
    if i ~= 1 && i ~= 399 && i ~= 400
        x_I(2*i) = (9*x_I(2*i-1)+9*x_I(2*i+1)-x_I(2*i-3)-x_I(2*i+3))/16;
    end
end
for i=1:400
    if i == 1
        x_Q(2*i-1) = x_Q(2*i);
    end
    if i == 2 || i == 400
        x_Q(2*i-1) = 0.5*(x_Q(2*i-2) + x_Q(2*i));
    end
    if i ~= 1 && i ~= 2 && i ~= 400
        x_Q(2*i-1) = (9*x_Q(2*i-2)+9*x_Q(2*i)-x_Q(2*i-4)-x_Q(2*i+2))/16;
    end
end
figure(4);
plot(n_bpsk,x_Q);grid on;title('正交支路信号');
figure(5);
plot(n_bpsk,x_I);grid on;title('同相支路信号');

实验结果

  仿真实验采用的信号为中频10kHz，初相位$0.3\pi$的正弦波，同时叠加有正态噪声。根据上述理论计算，信号的正交分量和同相分量都是直流分量，因为原信号的包络信号是直流的。正交支路$sin(0.3\pi )\approx 0.809$，同相支路$cos(0.3\pi )\approx 0.588$。从下面两图的结果可以看出，两支路信号的值大致是分布在理论计算值附近的。

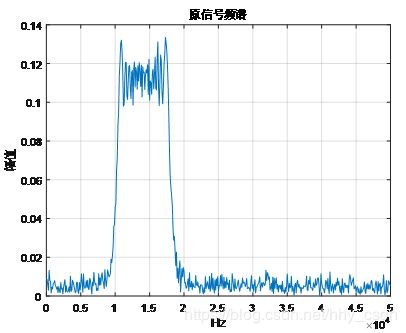
在前面的实验中已经表述过，LFM信号的频谱是一段起点不为零的连续波形。频谱的起点就是信号的初始频率$f_0$。在仿真实验中，我们设置$f_0=10kHz$，频率变化斜率为$k=800000Hz/s$，信号持续时间10ms，因此频谱末端为18kHz，如下图所示。

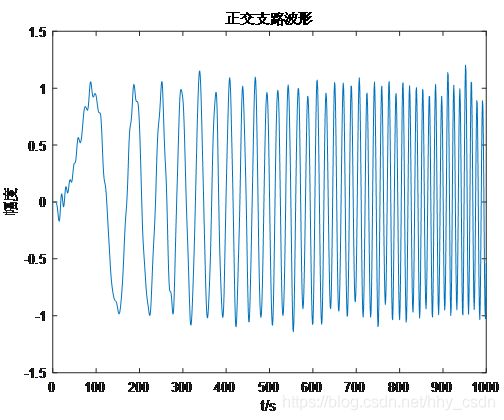
  经过检波处理，实际上是移除了信号的中频分量，将信号的频谱搬移到零频处。因此两个支路的频域波形如下所示。

  原始信号的波形如下所示。经过检波处理，支路信号的频率从零开始，因此起初的震荡是十分缓慢的，后期逐渐加快，不像原始信号，在一开始其频率就非常高。

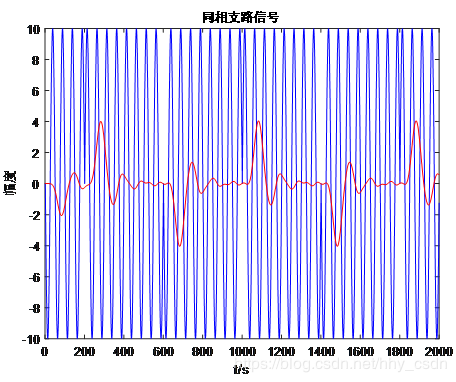
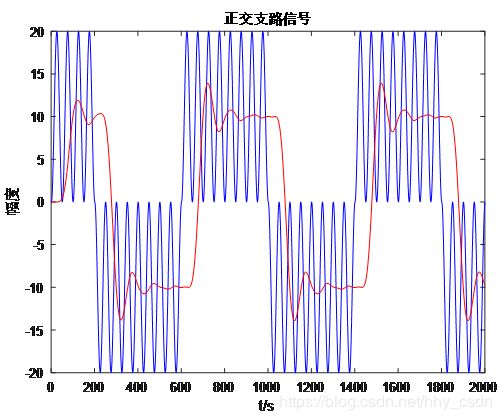
  BPSK信号在时域上可以看做是单频脉冲信号的拼接，只是基波是零相位或180°相位的正弦波信号。因此BPSK信号的两支路信号是不同的，正交支路检出直流分量，而同相分量只有二倍频信号，过低通滤波为零，所以体现为幅值为零的波形。