平衡二叉树思路分析及代码实现

基本介绍

1. 平衡二叉树也叫平衡二叉搜索树（Self-balancing binary searchtree）又被称为AVL树，可以保证查询效率较高。
2. 具有以下特点：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。平衡二又树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。
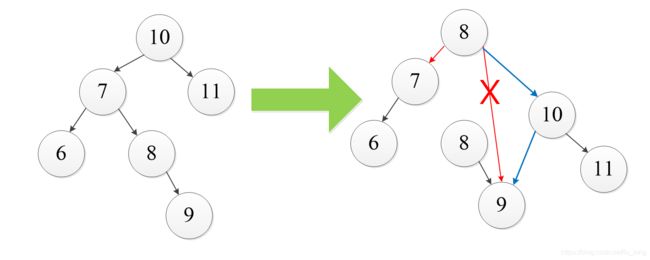
3. 举例说明：
   

应用案例(一)——单旋转（左旋转）

• 以数列{4，3，6，5，7，8}为例构建一颗平衡二叉树

问题： 当插入8时，rightHeight（）-leftHeight（）>1成立，此时，不再是一颗AVL树了.
怎么处理 ------ 进行左旋转
1.创建一个新的节点newNode（以4这个值创建），创建一个新的节点，值等于当前根节点的值
//把新节点的左子树设置为当前节点的左子树
2.newNode.left=left
//把新节点的右子树设置为当前节点的右子树的左子树
3.newNode.right =right.left；
//把当前节点的值换为右子节点的值
4.value=right.value；
//把当前节点的右子树设置成右子树的右子树
5.right=right.right；
//把当前节点的左子树设置为新节点
6.left=newLeft；

应用案例(二)——单旋转（右旋转）

• 以数列{10，12，8，9，6}为例构建一颗平衡二叉树

问题： 当插入6时，leftHeight（）-rightHeight（）>1成立，此时，不再是一颗AVL树了。
怎么处理 ------ 进行右旋转
就是降低左子树的高度。这里是将9这个节点，通过右旋转，到右子树。
1.创建一个新的节点newNode（以10这个值创建）创建一个新的节点，值等于当前根节点的值
//把新节点的右子树设置了当前节点的右子树
2.newNode.right=right
//把新节点的左子树设置为当前节点的左子树的右子树
3.newNode.left =left.right；
//把当前节点的值换为左子节点的值
4.value=left.value；
/把当前节点的左子树设置成左子树的左子树
5.left=left.left；
///把当前节点的右子树设置为新节点
6.right=newLeft；

应用案例(三)——双旋转

• 以数列{10, 11, 7, 6, 8, 9 }为例构建一颗平衡二叉树

问题： 当插入9时，经过左旋转或者右旋转后依旧不是一颗AVL树了。
分析

1. 当符号右旋转的条件时
2. 如果它的左子树的右子树高度大于它的左子树的高度
3. 先对当前这个结点的左节点进行左旋转
4. 在对当前结点进行右旋转的操作即可
   

代码实现

package com.avl;

public class AVLTreeDemo {

	public static void main(String[] args) {
		// int[] arr = { 4, 3, 6, 5, 7, 8 };
		// int[] arr = { 10, 12, 8, 9, 7, 6 };
		int[] arr = { 10, 11, 7, 6, 8, 9 };
		// 创建AVLTree对象
		AVLTree avlTree = new AVLTree();
		// 添加结点
		for (int i = 0; i < arr.length; i++) {
			avlTree.add(new Node(arr[i]));
		}

		// 遍历
		System.out.println("中序遍历");
		avlTree.infixOrder();

		System.out.println("【平衡处理】");
		System.out.println("树的高度=" + avlTree.getRoot().height());
		System.out.println("树的左子树高度=" + avlTree.getRoot().leftHeight());
		System.out.println("树的右子树高度=" + avlTree.getRoot().rightHeight());

	}

}

// 创建AVL树
class AVLTree {
	private Node root;

	public Node getRoot() {
		return root;
	}

	// 查找要所处的结点
	public Node search(int value) {
		if (root == null) {
			return null;
		} else {
			return root.search(value);
		}
	}

	// 查找父节点
	public Node searchParent(int value) {
		if (root == null) {
			return null;
		} else {
			return root.searchParent(value);
		}
	}

	/**
	 * @Method_Name:delRightTreeMin
	 * @Description:
	 * @param node
	 *            传入的结点(当做二叉排序树的根节点)
	 * @return int 以node为根节点的二叉排序树的最小结点的值
	 */
	public int delRightTreeMin(Node node) {
		Node target = node;
		// 循环查找左节点，就会找到最小值
		while (target.left != null) {
			target = target.left;
		}
		// 这是target就指向最小结点
		// 删除最小结点
		delNode(target.value);
		return target.value;

	}

	// 删除结点
	public void delNode(int value) {
		if (root == null) {
			return;
		} else {
			// 1.先找到要删除的结点
			Node targetNode = search(value);
			// 没有找到结点
			if (targetNode == null) {
				return;
			}
			// 如果当前二叉排序树只有一个节点
			if (root.left == null && root.right == null) {
				root = null;
				return;
			}

			// 找到targetNode的父节点
			Node parent = searchParent(value);
			// 如果要删除的是叶子结点
			if (targetNode.left == null && targetNode.right == null) {
				// 判断targetNode是父节点的左子节点还是右子节点
				if (parent.left != null && parent.left.value == value) {// 是左子节点
					parent.left = null;
				} else if (parent.right != null && parent.right.value == value) {// 是右子节点
					parent.right = null;
				}
			} else if (targetNode.left != null && targetNode.right != null) {// 删除有两颗子树的结点
				int minVal = delRightTreeMin(targetNode.right);
				targetNode.value = minVal;

			} else { // 删除只有一颗子树的结点
				// 如果要删除的结点有左子节点
				if (targetNode.left != null) {
					if (parent != null) {
						// 如果targetNode是parent的左子节点
						if (parent.left.value == value) {
							parent.left = targetNode.left;
						} else {// targetNode是parent的右子节点
							parent.right = targetNode.left;
						}
					} else {
						root = targetNode.left;
					}
				} else {// 要删除的结点有右子节点
					if (parent != null) {
						// 如果targetNode是parent的左子节点
						if (parent.left.value == value) {
							parent.left = targetNode.right;
						} else {// 如果targetNode是parent的右子节点
							parent.right = targetNode.right;
						}
					} else {
						root = targetNode.right;
					}
				}
			}
		}
	}

	// 添加节点
	public void add(Node node) {
		if (root == null) {
			root = node;// 如果root为空直接让root指向node
		} else {
			root.add(node);
		}
	}

	// 中序遍历
	public void infixOrder() {
		if (root != null) {
			root.infixOrder();
		} else {
			System.out.println("二叉排序树为空");
		}
	}
}

// 创建节点
class Node {
	int value;
	Node left;
	Node right;

	public Node(int value) {
		this.value = value;
	}

	// 返回左子树的高度
	public int leftHeight() {
		if (left == null) {
			return 0;
		}
		return left.height();
	}

	// 返回右子树的高度
	public int rightHeight() {
		if (right == null) {
			return 0;
		}
		return right.height();
	}

	// 返回当前节点为根节点的高度
	public int height() {
		return Math.max(left == null ? 0 : left.height(), right == null ? 0 : right.height()) + 1;
	}

	// 左旋转方法
	private void leftRotate() {
		// 创建新节点，以当前根节点创建
		Node newNode = new Node(value);
		// 把新节点的左子树设置为当前节点的左子树
		newNode.left = left;
		// 把新节点的右子树设置为当前节点的右子树的左子树
		newNode.right = right.left;
		// 把当前节点的值换为右子节点的值
		value = right.value;
		// 把当前节点的右子树设置成右子树的右子树
		right = right.right;
		// 把当前节点的左子树设置为新节点
		left = newNode;
	}

	// 右旋转
	private void rightRotate() {
		Node newNode = new Node(value);
		newNode.right = right;
		newNode.left = left.right;
		value = left.value;
		left = left.left;
		right = newNode;

	}

	// 查找要删除的结点
	/**
	 * @Method_Name:search
	 * @Description:查找要删除的结点
	 * @param value
	 *            要删除结点的值
	 * @return Node
	 */
	public Node search(int value) {
		if (value == this.value) {// 找到该节点
			return this;
		} else if (value < this.value) {// 如果查找的值小于当前节点，向左子树递归查找
			if (this.left == null) {
				return null;
			}
			return this.left.search(value);
		} else {// 如果查找的值不小于当前节点，向右子树递归查找
			if (this.right == null) {
				return null;
			}
			return this.right.search(value);
		}
	}

	// 查找要删除结点的父结点
	/**
	 * @Method_Name:searchParent
	 * @Description:查找要删除结点的父结点
	 * @param value
	 *            要找到的结点的值
	 * @return Node 返回结点要删除的父结点，没有就返回null
	 */
	public Node searchParent(int value) {
		// 如果当前节点就是要删除结点的父结点，就返回
		if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) {
			return this;
		} else {
			// 如果查找的值小于当前节点的值，并且当前节点的左子结点不为空
			if (value < this.value && this.left != null) {
				return this.left.searchParent(value);// 向左子树递归查找
			} else if (value >= this.value && this.right != null) {
				return this.right.searchParent(value);// 向右子树递归
			} else {
				return null;// 有找到父结点
			}
		}
	}

	@Override
	public String toString() {
		return "Node [value=" + value + "]";
	}

	// 添加节点
	// 递归添加，需要满足二叉排序树的要求
	public void add(Node node) {
		if (node == null) {
			return;
		}

		// 判断传入结点的值和当前子树的根节点值的关系
		if (node.value < this.value) {
			if (this.left == null) {
				this.left = node;
			} else {
				// 向左子树添加
				this.left.add(node);
			}
		} else {// 添加的大于当前节点的值
			if (this.right == null) {
				this.right = node;
			} else {
				// 向右子树添加
				this.right.add(node);
			}
		}
		// 当添加完一个节点后，(右子树的高度-左子树的高度)>1 ,左旋转
		if (rightHeight() - leftHeight() > 1) {
			// 如果它的右子树的左子树的高度大于它的右子树的右子树的高度
			if (right != null && right.leftHeight() > right.rightHeight()) {
				// 先对右子结点进行右旋转
				right.rightRotate();
				// 然后在对当前结点进行左旋转
				leftRotate();// 左旋转..
			} else {
				leftRotate();// 左旋转
			}
			return;// 必须要
		}
		// 当添加完一个节点后，(左子树的高度-右子树的高度)>1 ,右旋转
		if (leftHeight() - rightHeight() > 1) {
			// 如果它的左子树的右子树高度大于它的左子树的高度
			if (left != null && left.rightHeight() > left.leftHeight()) {
				// 先对当前这个结点的左节点进行左旋转
				left.leftRotate();
				// 再对当前结点进行右旋转
				rightRotate();// 右旋转
			} else {
				// 进行右旋转
				rightHeight();
			}
		}

	}

	// 中序遍历
	public void infixOrder() {
		if (this.left != null) {
			this.left.infixOrder();
		}
		System.out.println(this);
		if (this.right != null) {
			this.right.infixOrder();
		}
	}
}