浅谈线段树

大家好，给大家介绍完了树状数组（有兴趣的读者可以在我的博客文章中阅读），现在来给大家介绍另一种数据结构——线段树。它们结构都有共同点，但是线段树更为复杂，功能也更为强大，接下来就会一步一步向你介绍线段树的功能和用法。

线段树（Segment Tree）的简介：
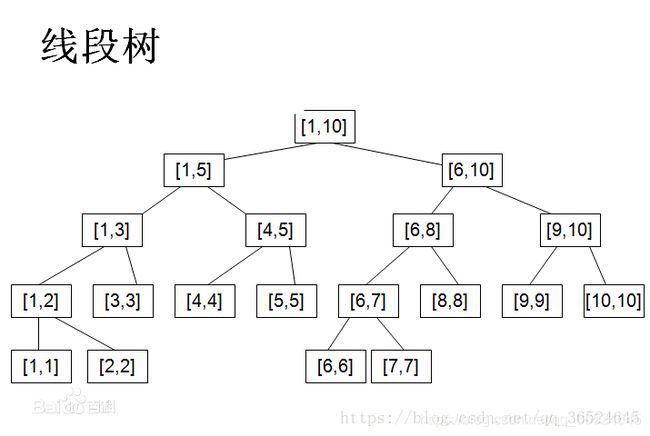
  线段树是一种二叉搜索树，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点，它基于分之思想，用于在线性区间上完成动态统计，它的思想主要是将线性的区间递归划分成长度相同的两段，直到叶子节点，每个叶子表示一个数据，向上每一层父亲节点都涵盖了所有儿子节点，模型图如下：

在图上，我们可以看出，它的根节点即为我们需要修改和统计的线段，它将其划分成两段子线段，运用了二分的思想mid=(l+r)/2,我们再来想想看一个节点应该包含什么数据，首先肯定是它的范围L和R，在就是一个数据域date，至于这个date存储什么数据，那就根据需要而定，例如可以存储这一段的最值，也可存储这一段的和等等，当然也可以都存储，无非就是多几个变量，基本的节点信息就是这些，然后再考虑一下用多大的数组来存储，根据上图，我们可以发现由于是二分的思想，所以不一定是理想的满二叉树，一个节点可能会有空的子节点，N个节点的满二叉树节点为N+N/2+N/4+...+1=2*N-1，然后再下面一层节点数为2N，要空余出来，所以存储1~N数组要开4*N，可以用一下代码表示：

struct Segment_tree
{
    int l,r;
    int date;
}node[SIZE*4];

 由此我们可以总结一下线段树节点的特点：

• 线段树每个节点代表着一个区间。
• 线段树的根节点表示统计范围区间1~n。
• 线段树每个叶子节点代表着一个数值。
• 对于每个除叶子节点外的节点[L,R],它的左子节点[L,mid],右子节点[mid+1,R]。
• 对于编号为i的节点，左子节点编号2*i，右子节点编号2*i+1。

由此我们可以递归建线段树，代码如下：

void Build_SegmentTree(int p,int L,int R)
{
    node[p].tag=0;node[p].sum=0;
    node[p].l=L,node[p].r=R;
    if(L==R){node[p].sum=num[L];return;}
    int mid=(L+R)/2;
    Build_SegmentTree(2*p,L,mid);
    Build_SegmentTree(2*p+1,mid+1,R);
    node[p].sum=node[2*p].sum+node[2*p+1].sum;
}

线段树经典例题：

已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数加上x

2.求出某区间每一个数的和

输入格式：

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个指令，具体如下：

1： 格式：1 x y k 含义：将区间[x,y]内每个数加上k

2： 格式：2 x y 含义：输出区间[x,y]内每个数的和

输出格式： 

输出包含若干行整数，即为所有指令2的结果。

  这道题是一个典型的线段树例题，当然同样可以用树状数组来做，用一个循环来修改[x,y]的叶子节点值，再用容斥原理来求出[x,y]的和，但考虑这样做法的时间复杂度T(n)=O((y-x)logn)，并不能满足100000的数据规模，所以来考虑线段树。在这道题中，考虑修改节点后改变的量，改变的是所有父亲节点，那么我们这里节点参数要带一个叫做“懒惰标记tag”的参数，用来表示我们对这个节点之下叶子节点的修改量，再用一个sum来表示叶子节点对父亲节点的增加量，线段树节点以及建树过程代码如下：
 

struct Segment_tree
{
    int l,r;
    long long sum,tag;
}node[SIZE*4];
void Build_SegmentTree(int p,int L,int R)
{
    node[p].tag=0;node[p].sum=0;
    node[p].l=L,node[p].r=R;
    if(L==R){node[p].sum=num[L];return;}
    int mid=(L+R)/2;
    Build_SegmentTree(2*p,L,mid);
    Build_SegmentTree(2*p+1,mid+1,R);
    node[p].sum=node[2*p].sum+node[2*p+1].sum;
}

  接下来思考对节点的修改，对于修改线段[L,R]，如果包含了当前节点的全部，那么给这个节点打上懒惰标记，加上这个节点所有的叶子数leave*变化量k，再递归的分别向左子节点和右子节点修改值，代码如下：

void Segment_update(int L,int R,int k,int rt)
{
    if(L<=node[rt].l&&R>=node[rt].r)
    {
        node[rt].tag+=k;
        node[rt].sum+=(long long)k*(node[rt].r-node[rt].l+1);
        return;
    }
    pushdown(rt);
    int mid=(node[rt].l+node[rt].r)/2;
    if(L<=mid) Segment_update(L,R,k,rt*2);
    if(R>mid) Segment_update(L,R,k,rt*2+1);
    node[rt].sum=node[rt*2].sum+node[rt*2+1].sum;
}

  读者可能发现了代码中有一个未知的函数pushdown()，这个函数便代表着懒惰标记下移，这下我们知道了为什么叫它懒惰标记了，因为如果不需要他，就没有必要一直递归到叶子节点来修改节点值，而是在父亲节点上标上对叶子节点的修改量，就是所谓的懒惰标记，当区间涉及到子节点线段时才下移懒惰标记来计算对于这一子段和的修改量，是不是很巧妙？pushdown函数代码如下：
 

void pushdown(int p)
{
    if(node[p].tag!=0)
    {
        node[p*2].sum+=node[p].tag*(node[p*2].r-node[p*2].l+1);
        node[p*2+1].sum+=node[p].tag*(node[p*2+1].r-node[p*2+1].l+1);
        node[p*2].tag+=node[p].tag;
        node[p*2+1].tag+=node[p].tag;
        node[p].tag=0;
    }
    return;
}

接下来就很简单了，递归的询问线段值，不多介绍，代码如下：

long long Segment_Query(int p,int L,int R)
{
    if(L<=node[p].l&&R>=node[p].r) return node[p].sum;
    pushdown(p);
    int mid=(node[p].l+node[p].r)/2;
    long long ans=0;
    if(L<=mid) ans+=Segment_Query(p*2,L,R);
    if(R>mid) ans+=Segment_Query(p*2+1,L,R);
    return ans;
}

完整的程序如下：

#include 
#define SIZE 100005
using namespace std;
int N,Q,num[SIZE];
struct Segment_tree
{
    int l,r;
    long long sum,tag;
}node[SIZE*4];
void Build_SegmentTree(int p,int L,int R)
{
    node[p].tag=0;node[p].sum=0;
    node[p].l=L,node[p].r=R;
    if(L==R){node[p].sum=num[L];return;}
    int mid=(L+R)/2;
    Build_SegmentTree(2*p,L,mid);
    Build_SegmentTree(2*p+1,mid+1,R);
    node[p].sum=node[2*p].sum+node[2*p+1].sum;
}
void pushdown(int p)
{
    if(node[p].tag!=0)
    {
        node[p*2].sum+=node[p].tag*(node[p*2].r-node[p*2].l+1);
        node[p*2+1].sum+=node[p].tag*(node[p*2+1].r-node[p*2+1].l+1);
        node[p*2].tag+=node[p].tag;
        node[p*2+1].tag+=node[p].tag;
        node[p].tag=0;
    }
    return;
}
void Segment_update(int L,int R,int k,int rt)
{
    if(L<=node[rt].l&&R>=node[rt].r)
    {
        node[rt].tag+=k;
        node[rt].sum+=(long long)k*(node[rt].r-node[rt].l+1);
        return;
    }
    pushdown(rt);
    int mid=(node[rt].l+node[rt].r)/2;
    if(L<=mid) Segment_update(L,R,k,rt*2);
    if(R>mid) Segment_update(L,R,k,rt*2+1);
    node[rt].sum=node[rt*2].sum+node[rt*2+1].sum;
}
long long Segment_Query(int p,int L,int R)
{
    if(L<=node[p].l&&R>=node[p].r) return node[p].sum;
    pushdown(p);
    int mid=(node[p].l+node[p].r)/2;
    long long ans=0;
    if(L<=mid) ans+=Segment_Query(p*2,L,R);
    if(R>mid) ans+=Segment_Query(p*2+1,L,R);
    return ans;
}
int main()
{
    cin>>N>>Q;
    for(int i=1;i<=N;i++) cin>>num[i];
    Build_SegmentTree(1,1,N);
    for(int i=1;i<=Q;i++)
    {
        int code,par1,par2,par3;
        scanf("%d",&code);
        if(code==1){scanf("%d%d%d",&par1,&par2,&par3);Segment_update(par1,par2,par3,1);}
        if(code==2){scanf("%d%d",&par1,&par2);printf("%lld\n",Segment_Query(1,par1,par2));}
    }
    return 0;
}

根据以上的介绍，想必大家对线段树已经有了初步的了解。其实线段树就是解决某空间中的动态统计问题的工具，是一种数据结构。博主QQ1552611369，有兴趣的读者可以加我QQ。