2020HDU暑假多校第2场

题目地址：http://acm.hdu.edu.cn/search.php?field=problem&key=2020+Multi-University+Training+Contest+2&source=1&searchmode=source

1001：Total Eclipse

题意：给你$n$个点，$m$条边，点有点权。每次你最多可以选择$k$个相连的点，使得这些点的点权全部减1，问你最少经过几次操作可以将所有点的点权全部变成0。

思路：首先我们考虑正像的做法，每次选取极大连通块，之后将所有点的点权全部减去连通块里最小的点权，这样这个大的连通块就可以分裂成多个更小的连通块…重复上述操作，直到所有点的点权全部是0。这样我们可以看到时间复杂度特别大，几乎是不能接受的。
所以我们可以考虑将所有点按照点权从大到小排序，之后我们每加入一个点答案就加上
$$当前连通块的个数\ast (当前点的点权-下一个点的点权)$$
为什么呢？
我们考虑使用以下的样例来模拟一下算法流程

首先，我们将点按照点权从大到小排序，得到

6 5 4 3 2 1

1、我们加入6这个点；
2、我们再加入5这个点，我们可以看到此时图中有两个连通块，如下图所示：

那我们就可以考虑"让6变成5"，所需要的代价就是$1\ast (6-5)$此时只有一个连通块需要变这样图中我们就可以看成是两块点权为5的连通块；
3、接下来在加入4，如下：

这样我们就可以看到我们需要将两块点权为5的连通块变成4，需要的代价就是$2\ast (5-4)$，又6和4这两条边是相连的，那么我们就可以看成是两块点权为4的连通块，如下图：

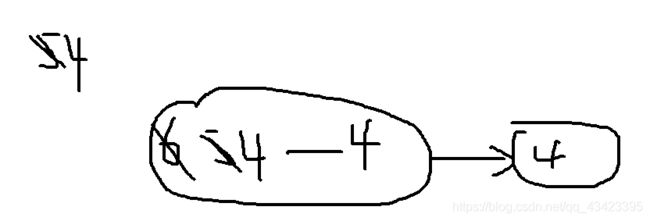
4、同理，接下来我们加入3，就相当于有两个点权为4的连通块要变成3，代价为$2\ast (4-3)$，而且4和三相连，这样就相当于现在剩下的就是两个点权为3的连通块.

…

依次类推，我们最后就可以得到数个点权为0的连通块，每个过程的累加和便是答案。

代码如下：

#define _CRT_SECURE_NO_WARNINGS 1

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;

#define LL long long
#define pii pair
#define sd(x) scanf("%d",&x)
#define slld(x) scanf("%lld",&x)
#define pd(x) printf("%d\n",x)
#define plld(x) printf("%lld\n",x)
#define rep(i,a,b) for(int i = (a) ; i <= (b) ; i++)
#define per(i,a,b) for(int i = (a) ; i >= (b) ; i--)
#define mem(a) memset(a,0,sizeof(a))
#define lson l , m , rt << 1
#define rson m + 1 , r , rt << 1 | 1
#define fast_io ios::sync_with_stdio(false)

const int INF = 1e9 + 10;
const LL mod = 998244353;
const int maxn = 1e5 + 7;

int head[maxn << 2];
struct Edge {
    int to,next;
} edge[maxn << 2];
int tot;

void init() {
    memset(head,-1,sizeof(head));
    tot = 0;
}

void addedge(int u,int v) {
    edge[tot].to = v;
    edge[tot].next = head[u];
    head[u] = tot++;
}

int f[maxn];

int Find(int x) {
    if(x == f[x]) return x;
    else return f[x] = Find(f[x]);
}

struct node {
    int val,id;
} a[maxn];

bool cmp(node aa,node bb) {
    return aa.val > bb.val;
}

int vis[maxn];

int main() {
    int T;
    sd(T);
    while(T--) {
        int n,m;
        sd(n),sd(m);
        rep(i,1,n) {
            sd(a[i].val);
            f[i] = a[i].id = i;
        }
        init();
        rep(i,1,m) {
            int u,v;
            sd(u),sd(v);
            addedge(u,v),addedge(v,u);
        }
        sort(a+1,a+n+1,cmp);
        a[n+1].val = 0;
        LL ans = 0;
        LL res = 0;
        mem(vis);
        rep(i,1,n) {
            int u = a[i].id;
            vis[u] = 1;
            res++;
            for(int j = head[u] ; j != -1 ; j = edge[j].next) {
                int v = edge[j].to;
                int t1 = Find(u);
                int t2 = Find(v);
                if(vis[v] && t1 != t2) {
                    f[t1] = t2;
                    res--;
                }
            }
            ans += res * (a[i].val - a[i+1].val) * 1LL;
            // cout << "i = " << i << " ans = " << ans << " " << a[i].val << " " << a[i+1].val << endl;
        }
        plld(ans);
    }
    return 0;
}