旅行商问题动态规划解法(python版)

2019年华为实习生第二场笔试第二题是个旅行商问题，虽然只有5个点可以import itertools产生排列遍历5！=120情况求解（当然也可以写个递归自己生成排列），还是查了下动态规划的解法。

原理来自：旅行推销商问题TSP的动态规划解法

实现来自：Python求解tsp问题（动态规划，简单易懂）

实现里做了小小的修改：

def __init__(self,X,start_node):
        self.X = X #距离矩阵
        self.start_node = start_node #开始的节点
        #len(self.X)加多-1
        self.array = [[0]*(2**(len(self.X)-1)) for i in range(len(self.X))] 

    def transfer(self, sets):
        su = 0
        for s in sets:
            # s改成s-1
            su = su + 2**(s-1) # 二进制转换
        return su

完整代码：

# tsp问题
class Solution:
    def __init__(self,X,start_node):
        self.X = X #距离矩阵
        self.start_node = start_node #开始的节点
        self.array = [[0]*(2**(len(self.X)-1)) for i in range(len(self.X))] #记录处于x节点，未经历M个节点时，矩阵储存x的下一步是M中哪个节点

    def transfer(self, sets):
        su = 0
        for s in sets:
            su = su + 2**(s-1) # 二进制转换
        return su

    # tsp总接口
    def tsp(self):
        s = self.start_node
        num = len(self.X)
        cities = list(range(num)) #形成节点的集合
        # past_sets = [s] #已遍历节点集合
        cities.pop(cities.index(s)) #构建未经历节点的集合
        node = s #初始节点
        return self.solve(node, cities) #求解函数

    def solve(self, node, future_sets):
        # 迭代终止条件，表示没有了未遍历节点，直接连接当前节点和起点即可
        if len(future_sets) == 0:
            return self.X[node][self.start_node]
        d = 99999
        # node如果经过future_sets中节点，最后回到原点的距离
        distance = []
        # 遍历未经历的节点
        for i in range(len(future_sets)):
            s_i = future_sets[i]
            copy = future_sets[:]
            copy.pop(i) # 删除第i个节点，认为已经完成对其的访问
            distance.append(self.X[node][s_i] + self.solve(s_i,copy))
        # 动态规划递推方程，利用递归
        d = min(distance)
        # node需要连接的下一个节点
        next_one = future_sets[distance.index(d)]
        # 未遍历节点集合
        c = self.transfer(future_sets)
        # 回溯矩阵，（当前节点，未遍历节点集合）——>下一个节点
        self.array[node][c] = next_one
        return d

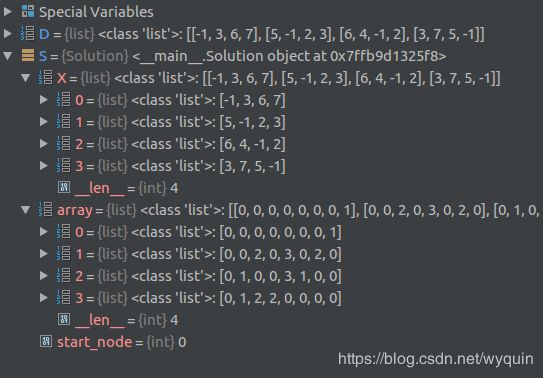
D=[
[-1, 3, 6, 7],
[ 5,-1, 2, 3],
[ 6, 4,-1, 2],
[ 3, 7, 5,-1]]

S = Solution(D,0)
print(S.tsp())
# 开始回溯
M = S.array
lists = list(range(len(S.X)))
start = S.start_node
while len(lists) > 0:
    lists.pop(lists.index(start))
    m = S.transfer(lists)
    next_node = S.array[start][m]
    print(start,"--->" ,next_node)
    start = next_node

递归生成排列的简单例子

#include
typedef char Type;
void Perm(Type a[], int k, int n);
 
void main()
{
	Type array[3]={'a','b','c'};
	Perm(array,0,2);
}
 
void Perm(Type a[], int k, int n)
{
	if (k==n) {	//输出排列
		for (int i=0; i<=n; i++) cout << a[i]<<" ";
		cout << endl;
	}
	else		//a[k:n]中包含多个排列，递归生产这些排列
		for (int i=k; i<=n; i++) {
			 Type t = a[k]; a[k] = a[i]; a[i]=t;
			 Perm(a, k+1, n);
			 //a[k+1:n]的所有排列
			 t = a[k]; a[k] = a[i]; a[i] = t;
		}
}

也可以import itertools库

# -*- coding:utf-8 -*-
import itertools
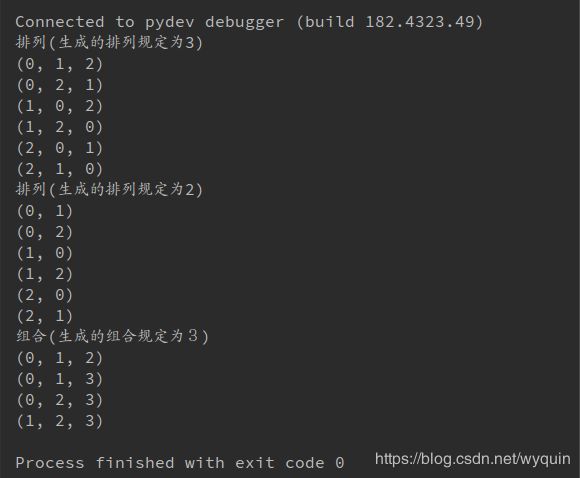
print('排列(生成的排列规定为3)')
for i in itertools.permutations([0,1,2], 3):
    print(i)
print('排列(生成的排列规定为2)')
for i in itertools.permutations([0,1,2], 2):
    print(i)
print('组合(生成的组合规定为３)')
for i in itertools.combinations([0,1,2,3], 3):
    print (i)