hdu2255--KM算法
奔小康赚大钱
Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 2474 Accepted Submission(s): 1087
这可是一件大事,关系到人民的住房问题啊。村里共有n间房间,刚好有n家老百姓,考虑到每家都要有房住(如果有老百姓没房子住的话,容易引起不安定因素),每家必须分配到一间房子且只能得到一间房子。
另一方面,村长和另外的村领导希望得到最大的效益,这样村里的机构才会有钱.由于老百姓都比较富裕,他们都能对每一间房子在他们的经济范围内出一定的价格,比如有3间房子,一家老百姓可以对第一间出10万,对第2间出2万,对第3间出20万.(当然是在他们的经济范围内).现在这个问题就是村领导怎样分配房子才能使收入最大.(村民即使有钱购买一间房子但不一定能买到,要看村领导分配的).
对于这里给出 一:基本概念 二:算法原理和语言描述 三:结合图形理解KM算法过程
一.
首先给出一些摘要知识点以及算法的语言描述(如果前面看过前辈们的,只是对于算法过程不了解的可以直接看后面结合图形的算法详细解说,这里归纳个人觉得对于一个小白学习有用的知识点)
首先
1. 完备匹配:如下图,设G=
![]()
那么对于V1的点都有与之对应的匹配,就是完备匹配(就是完全把V1的点都匹配完)
2. 可行顶标:对于左边的点设 lx[MAX] 数组, 对于右边的点设 ly[MAX] 数组,Vi,j 表示 vi 到 vj 的权值(这里的原因是为了求解最优完备匹配,可以在下面理解)
3. 相等子图:相等子图为完备匹配中所有的匹配(就是全部的V1的点,和与之匹配的V2中的点),但是对于边就只包含lx[i] + ly[j] = V(i,j)的边
4.最优完备匹配:那么这个就是我们的目的啦,对于上面说的完备匹配之下要求最优,那么结合相等子图来就有若由二分图中所有满足A[i]+B[j]=w[i,j]的边(i,j)构成的相等子图有完备匹配,那么这个完备匹配就是二分图的最大权匹配。
这个定理是显然的。因为对于二分图的任意一个匹配,如果它包含于相等子图,那么它的边权和等于所有顶点的顶标和;如果它有的边不包含于相等子图,那么它的边权和小于所有顶点的顶标和。所以相等子图的完备匹配一定是二分图的最大权匹配。
5. 交错树:这里是在对V1中的一个顶点进行匹配的时候所标记过得V1、V2的点和与之的连线,形成的一个像树装的图
二:
那么在了解了以上的基本概念之后,就来接触KM算法
1.首先基本的原理:该算法是通过给每个顶点一个标号(叫做顶标)来把求最大权匹配的问题转化为求完备匹配的问题的。设顶点V1的顶标为lx[ i ],V2顶点的顶标为ly[ j ],顶点V1的 i 与V2的 j 之间的边权为V[i,j]。在算法执行过程中的任一时刻,对于任一条边(i,j),lx[ i ]+ly[j]>=V[i,j]始终成立。
2.基本流程:
(1).初始时为了使lx[ i ]+ly[j]>=V[i,j]恒成立,将V1的点的标号记为与其相连边的最大边权值,V2的点标号全记为0
(2)用匈牙利算法在相等子图寻找完备匹配
(3)若未找到完备匹配则修改可行顶标的值 ,扩充相等子图
(4)重复(2)(3)直到找到相等子图的完备匹配为止
3.这里值得注意的是找完备匹配不难理解,主要是进行可行顶标的修改扩充相等子图,有:
引用:朴素的实现方法,时间复杂度为O(n4)——需要找O(n)次增广路, 每次增广最多需要修改O(n)次顶 标,每次修改顶标时由于要枚举边来求d值,复杂度为O(n2)。实际上KM算法的复杂度是可以做到O(n3)的。我们给每个Y顶点一个“松弛量”函数 slack,每次开始找增广路时初始化为无穷大。在寻找增广路的过程中,检查边(i,j)时,如果它不在相等子图中,则让slack[j]变成原值与A [i]+B[j]-w[i,j]的较小值。这样,在修改顶标时,取所有不在交错树中的Y顶点的slack值中的最小值作为d值即可。但还要注意一点:修改 顶标后,要把所有的slack值都减去d。
-----------------------------------------------------------------------------------------------------------------------
三:那么这里我们 就结合图形来理解扩充相等子图以及KM的算法过程
(可以结合模板代码看)
这里结合hdu2255:如果对应有案例
3
2 1 1
3 2 1
1 1 1
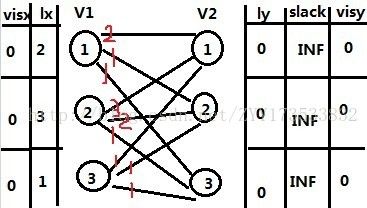
首先给出以下图:(V1,V2,V[i,j])v[i,j]表示边的权值
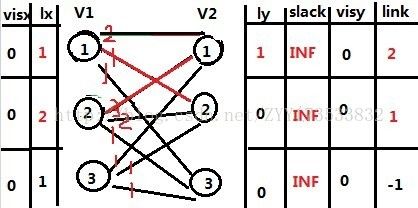
那么首先就是进行V1中的1的匹配,得下图 (INF表示无穷大)
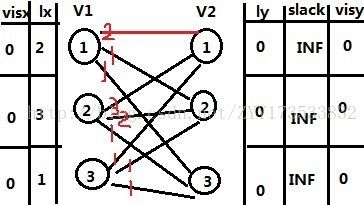
用红色的边代表匹配,这里对于V1的1能顺利一次匹配成功,就没有更改vis 的一些值,(小小的偷懒),那么下面就要对V1的2号顶点进行匹配,那么此过程中我们,我们首先考虑V2的1号点,发现它被V1的1号匹配了,那么就先把V1的1号赶走去和V2其他的几个点尝试匹配,并且在这个过程中我们会修改上图如下:
对于这一次匹配的过程中我们发现形成了一个上面说的交错树,那么对于V1的2号匹配失败之后我们就开始了修改顶标并扩充相等子图的操作,(注意此过程我们找出了 lx[i]+ly[j]-V[i,j] 的最小存于slack中,我们扩充的过程中找一次找到最小的即可)
那么首先我们要找不在交叉树中的V2的 j 点中slack[j]最小的 为 d=1
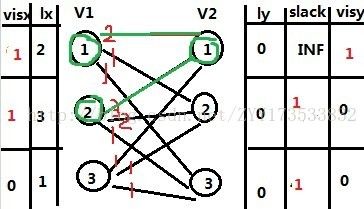
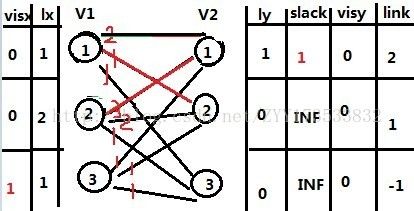
那么修改之后再一次匹配之前如下图:
那么我们发现lx[1]+ly[1]-V[1,1]没有变,lx[2]+ly[1]-V[2,1]也没有变,但是我们可以发现其他的lx[1]与lx[2]与其他的ly的和减小啦,那么V1的2号再次匹配的过程的时候就在考虑V2的1号的时候,发现V2的1号匹配者V1的1号可以去匹配V2的2号,这里就是扩充了一条边,那么这里就匹配成如下图:
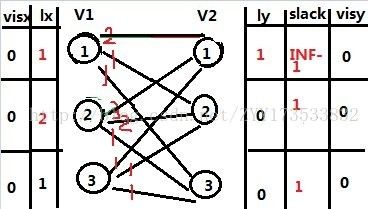
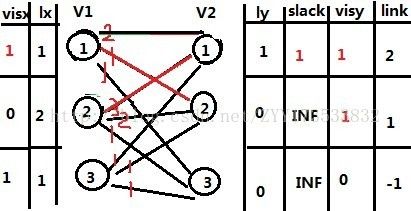
那么下面还有一个V1的顶点3,这个看起来可能第一感觉会说,直接匹配V2的3就是的,但是实际上KM的算法过程不是那么简单的,那么我们来一步步的模拟,首先,我们V1的3号去尝试匹配V2的1号,发现lx[3]+ly[1]-V[3,1]=1,那么匹配失败,更新如下图:
那么V1的3号就再考虑V2的2,此时有lx[3]+ly[2]-V[3,2]=0,但是发现V2的2早被V1的1匹配了(link[2]=1),那么根据匈牙利算法,把V1的1赶走去尝试与V2的其他点匹配,那么此时我们先关注V1的1,现在它可以考虑V2的1号,发现lx[1]+ly[1]-V[1,1]=0,但是此时V2的1号被V1的2号匹配啦(link[1]=2),那么同样根据匈牙利算法,把V1的2号赶走,那么此时如下图:(注意红的色部分的值变化)
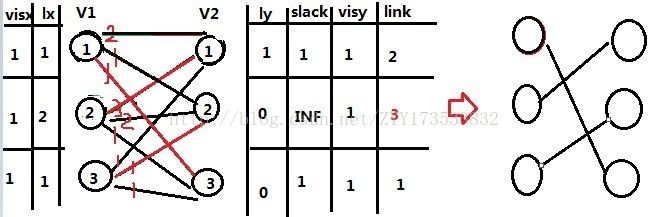
那么在此图的基础上,我们把关注V1的2号,发现只有V2的3号没有访问过,那么尝试匹配发现lx[2]+ly[3]-V[2,3]=1,匹配失败,那么V1的2号无处可去,回溯到被赶走的V1的1号,它发现赶不走V2的1的匹配者,那么就自己再找V2中别的人匹配,发现V2的2号被访问过啦,那么就找V2的3,此时发现能匹配,那么自己马上占领这里,那么此时就再回溯到V1的3,因为它把占领V2-2号的人赶到V2-1去了,所以自己就占领这里,那么如下图:
//421MS 616K 1711 B
#include
#include
#include
using namespace std;
#define MAX 310
#define INF 1<<25
#define clr(x) memset(x,0,sizeof(x))
/**注:发生矛盾,即几个居民同抢一个房子**/
int w[MAX][MAX];
int n;
int lx[MAX],ly[MAX];
int link[MAX];
int slack[MAX];
int visx[MAX],visy[MAX];
bool dfs(int x)
{
visx[x]=1; /****得到发生矛盾的居民集合****/
for(int y=1;y<=n;y++) /**这个居民,每个房子都去试一试!(找到就退出)**/
{
if(visy[y]) /****一个房子不需要重复访问****/
continue;
int t=lx[x]+ly[y]-w[x][y];/****按这个标准去用-匈牙利算法***/
if(t==0)/**t==0标志这个房子可以给这位居民**/
{
visy[y]=1;
if(link[y]==0||dfs(link[y])) /****这房子没人住 或 可以让住这个房子的人去找另外的房子住****/
{
link[y]=x; return true;/**那么就可以让这位居民住进来**/
}
}
else if(slack[y]>t)/**否则这个房子不能给这位居民!**/
slack[y]=t;/***就要找到这个房子要松弛多少才能够给这位居民***/
/***且当有多个居民都对这个房子有松弛量时,要找到最小的。****/
}
return false;
}
int KM()
{
clr(lx);
clr(ly);
clr(link);
/*****首先把每个居民出的钱最多的那个房子赋给它******/
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(lx[i]slack[k])
d=slack[k]; /****找到最小松弛量*****/
for(int k=1;k<=n;k++)/****松弛操作-使发生矛盾的居民有更多选择*****/
{
if(visx[k]) /*****将矛盾居民的要求降低,使他们有更多可房子选择*****/
lx[k]-=d;
if(visy[k]) /****使发生矛盾的房子在下一个子图,保持矛盾(即保持原子图性质)*****/
ly[k]+=d;
}
}
}
int ans=0;
for(int i=1;i<=n;i++)
ans+=w[link[i]][i];
return ans;
}
int main()
{
while(~scanf("%d",&n))
{
clr(w);//每个案列都要重新置0;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
scanf("%d",&w[i][j]);//输入每边权值
printf("%d\n",KM());
}
return 0;
}