⭐ 李宏毅2020机器学习作业2-Classification：年收入二分类

更多作业，请查看⭐ 李宏毅2020机器学习资料汇总

0 作业链接

直接在李宏毅课程主页可以找到作业：

• 李宏毅的课程网页：点击此处跳转

如果你打不开colab，下方是搬运的jupyter notebook文件和助教的说明ppt：

• 2020版课后作业范例和作业说明：点击此处跳转
• 数据链接：https://pan.baidu.com/s/1xWVKnm4P6bBawASzLYskaw 提取码：akti
• kaggle平台数据：点击此处跳转

1 作业说明

环境

• jupyter notebook
• python3

任务说明

二元分类是机器学习中最基础的问题之一。在本次作业中，需要写一个线性二元分类器，根据人们的个人信息，判断其年收入是否高于 50,000 美元。作业将用 logistic regression 与 generative model两种模型来实现目标，模型差异可见李宏毅老师的课程视频与ppt。

数据说明

从百度网盘下载data.tar.gz文件，解压。
文件目录树如下：

│  hw2_classification.ipynb
│  
└─data
        sample_submission.csv
        test_no_label.csv
        train.csv
        X_test
        X_train
        Y_train

这份数据集来自UCI Machine Learning Repository 的 Census-Income (KDD) Data Set，train.csv、test_no_label.csv、sample_submission.csv是数据集中原有的数据。本次作业只需要X_test、X_train、Y_train这三个文件。

本课程助教对原数据进行了清洗：

• 移除了一些不必要的数据
• 对离散值进行了one-hot编码

离散特征进行one-hot编码后，编码后的特征，其实每一维度的特征都可以看做是连续的特征。就可以跟对连续型特征的归一化方法一样，对每一维特征进行归一化。比如归一化到[-1,1]，或者归一化到均值为0,方差为1。
——————————————————————————
摘自特征工程——连续特征与离散特征处理方法

• 稍微平衡了正负标记的数据的比例

打开X_train与X_test格式相同，以Notepad++打开X_train查看文件格式：

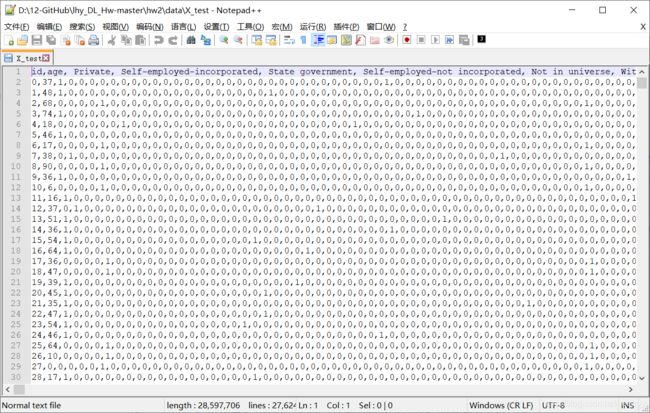
是一个类似csv格式的文件，第一行是表头，从第二行开始是具体数据。表头是人们的个人信息，比如年龄、性别、学历、婚姻状况、孩子个数等等。

再用Notepad++打开Y_train文件，进行查看：

只有两列，第一列是人的编号（ID），第二列是一个label——如果年收入＞50K美元，label就是1；如果年收入≤50K美元，label就是0.

最终，预测结果的保存格式为：第一行表头，总共两列，第一列是id，第二列是label.

作业概述

输入：人们的个人信息

输出：0（年收入≤50K）或1（年收入＞50K）

模型： logistic regression 或者 generative model

2 原始代码

2.0 数据准备

导入数据

读入X_train、Y_train、X_test三个文件，输出文件命名为output_{}.csv

import numpy as np

np.random.seed(0)
X_train_fpath = './data/X_train'
Y_train_fpath = './data/Y_train'
X_test_fpath = './data/X_test'
output_fpath = './output_{}.csv'

# 把csv文件转换成numpy的数组
with open(X_train_fpath) as f:
    next(f)
    X_train = np.array([line.strip('\n').split(',')[1:] for line in f], dtype = float)
with open(Y_train_fpath) as f:
    next(f)
    Y_train = np.array([line.strip('\n').split(',')[1] for line in f], dtype = float)
with open(X_test_fpath) as f:
    next(f)
    X_test = np.array([line.strip('\n').split(',')[1:] for line in f], dtype = float)

标准化（Normalization）

Normalization和Standardization分别被翻译成归一化和标准化，其实是有问题的，很容易被混淆。实际上，两者可以统称为标准化（Normalization），$x=\frac{x-\mu }{\sigma }$叫做z-score normalization，而$x=\frac{x-x_{min}}{x_{max}-x_{min}}$又叫做min-max normalization，网上的某些资料有点问题。

定义一个标准化函数_normalize()：

• train：bool变量，标记输入的X是否是训练集。
• specified_column：定义了需要被标准化的列。如果输入为None，则表示所有列都需要被标准化。
• X_mean：训练集中每一列的均值。
• X_std：训练集中每一列的方差。

然后，对X_train和X_test分别调用该函数，完成标准化。

def _normalize(X, train = True, specified_column = None, X_mean = None, X_std = None):
    # This function normalizes specific columns of X.
    # The mean and standard variance of training data will be reused when processing testing data.
    #
    # Arguments:
    #     X: data to be processed
    #     train: 'True' when processing training data, 'False' for testing data
    #     specific_column: indexes of the columns that will be normalized. If 'None', all columns
    #         will be normalized.
    #     X_mean: mean value of training data, used when train = 'False'
    #     X_std: standard deviation of training data, used when train = 'False'
    # Outputs:
    #     X: normalized data
    #     X_mean: computed mean value of training data
    #     X_std: computed standard deviation of training data

    if specified_column == None:
        specified_column = np.arange(X.shape[1])
        # print(specified_column)
        # 输出列的ID：
        #[  0   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16  17
        #  18  19  20  21  22  23  24  25  26  27  28  29  30  31  32  33  34  35
        # ...
        # 504 505 506 507 508 509]
    if train:
        X_mean = np.mean(X[:, specified_column] ,0).reshape(1, -1)
        X_std  = np.std(X[:, specified_column], 0).reshape(1, -1)

    X[:,specified_column] = (X[:, specified_column] - X_mean) / (X_std + 1e-8) #1e-8防止除零
     
    return X, X_mean, X_std


# 标准化训练数据和测试数据
X_train, X_mean, X_std = _normalize(X_train, train = True)
X_test, _, _= _normalize(X_test, train = False, specified_column = None, X_mean = X_mean, X_std = X_std)
# 用 _ 这个变量来存储函数返回的无用值

分割测试集与验证集

Development set is also called development set or sometimes called hold out cross validation set. ——摘自吴恩达的解释
这里的Development set即为验证集。
——————————————————
详情可见：deeplearning中的train set（训练集），development set（开发集） ，test set（测试集）的区别

对原来的X_train进行分割，分割比例为train:dev = 9:1。这里没有shuffle，是固定分割。

def _train_dev_split(X, Y, dev_ratio = 0.25):
    # This function spilts data into training set and development set.
    train_size = int(len(X) * (1 - dev_ratio))
    return X[:train_size], Y[:train_size], X[train_size:], Y[train_size:]
 
# 把数据分成训练集和验证集
dev_ratio = 0.1
X_train, Y_train, X_dev, Y_dev = _train_dev_split(X_train, Y_train, dev_ratio = dev_ratio)

train_size = X_train.shape[0]
dev_size = X_dev.shape[0]
test_size = X_test.shape[0]
data_dim = X_train.shape[1]
print('Size of training set: {}'.format(train_size))
print('Size of development set: {}'.format(dev_size))
print('Size of testing set: {}'.format(test_size))
print('Dimension of data: {}'.format(data_dim))

Out：
Size of training set: 48830
Size of development set: 5426
Size of testing set: 27622
Dimension of data: 510

一些有用的函数定义

• _shuffle(X,Y)：X和Y是两个数组，如果分别随机打乱X和Y，那么X和Y的对应关系就会被破坏。所以，这里生成行的编号，对行的编号进行打乱，就可以获得一一对应的打乱后的X和Y.

• _sigmoid(z)：$\sigma (z)$函数
  关于np.clip(a,x1,x2)，其中a是一个数组，后面两个参数x1和x2分别表示最小和最大值。比如：

  x = np.array([1,2,3,5,6,7,8,9])
  np.clip(x,3,8)
  # Out:
  # array([3, 3, 3, 5, 6, 7, 8, 8])
  

• _f(X,w,b)：Logistic Regression的函数$f_{w,b}(X)=\sigma (\mathbf{w}\cdot X+b)$，参数是权重$w$和偏差$b$.

• _predict(X,w,b)：根据$X$,$w$,$b$的值，计算预测值$y=f_{w,b}(X)$。因为$f_{w,b}(X)=\sigma (\mathbf{w}\cdot X+b)=\frac{1}{1+e^{-(\mathbf{w}\cdot X+b)}}$计算后，得到的值是一个(0,1)之间的数值，而预测值$y$应该是一个标签，0或者1。因此，需要np.round()函数：当$y\ge 0.5$时，令$y=1$；当$y<0.5$时，令$y=0$.

• _accuracy(Y_pred,Y_label)：评价预测值Y_pred和真实值Y_label差距的指标：

  • Y_label=0，Y_pred=0，正确预测，$1-|Y_{pred}-Y_{label}|=1$
  • Y_label=0，Y_pred=1，错误预测，$1-|Y_{pred}-Y_{label}|=0$
  • Y_label=1，Y_pred=0，错误预测，$1-|Y_{pred}-Y_{label}|=0$
  • Y_label=1，Y_pred=1，正确预测，$1-|Y_{pred}-Y_{label}|=1$
    $acc=1-|Y_{pred}-Y_{label}|$，acc越大，表示正确率越高。

def _shuffle(X, Y):
    # This function shuffles two equal-length list/array, X and Y, together.
    randomize = np.arange(len(X))
    np.random.shuffle(randomize)
    return (X[randomize], Y[randomize])

def _sigmoid(z):
    # Sigmoid function can be used to calculate probability.
    # To avoid overflow, minimum/maximum output value is set.
    return np.clip(1 / (1.0 + np.exp(-z)), 1e-8, 1 - (1e-8))

def _f(X, w, b):
    # This is the logistic regression function, parameterized by w and b
    #
    # Arguements:
    #     X: input data, shape = [batch_size, data_dimension]
    #     w: weight vector, shape = [data_dimension, ]
    #     b: bias, scalar
    # Output:
    #     predicted probability of each row of X being positively labeled, shape = [batch_size, ]
    return _sigmoid(np.matmul(X, w) + b)

def _predict(X, w, b):
    # This function returns a truth value prediction for each row of X 
    # by rounding the result of logistic regression function.
    return np.round(_f(X, w, b)).astype(np.int)
    
def _accuracy(Y_pred, Y_label):
    # This function calculates prediction accuracy
    acc = 1 - np.mean(np.abs(Y_pred - Y_label))
    return acc

2.1 Logistic Regression

第n个训练数据为$(x^n,{\hat{y}}^n)$，$x^n=[x_1^n,x_2^n,...,x_i^n,...]$（$x^n$并不是n次方，而是指第n个训练数据），真值${\hat{y}}^n$是0或1。

预测值$y^n=f_{w,b}(x^n)=\sigma (\mathbf{w}\cdot x^n+b)=\frac{1}{1+e^{-(\mathbf{w}\cdot x^n+b)}}=\frac{1}{1+e^{-(\sum w_i{x}_i^n+b)}}$

令$z=\mathbf{w}\cdot x^n+b=\sum w_i{x}_i^n+b$，则$y^n=f_{w,b}(x^n)=\sigma (z)=\frac{1}{1+e^{-z}}$

损失函数（Loss Function）

$$w^{\ast },b^{\ast }=\arg \underset{w,b}{\max }L(w,b)=\arg \underset{w,b}{\min }(-\ln L(w,b))$$

对Logistic Regression的损失函数$L(f)$取对数$\ln$并乘以-1。最优参数$w^{\ast }$、$b^{\ast }$从最大化$L(w,b)$变成了最小化$-\ln L(w,b)$。$C(f_{w,b}(x^n),{\hat{y}}^n)$是交叉熵：

$$\begin{array}{rl}-\ln L(f)& =-\ln L(w,b)\\ & =\sum _{n}C(f_{w,b}(x^n),{\hat{y}}^n)\\ & =\sum _n\left(-{\hat{y}}^n\ln f_{w,b}\left(x^n\right)-\left(1-{\hat{y}}^n\right)\ln \left(1-f_{w,b}\left(x^n\right)\right)\right)\\ & =-\sum _n\left({\hat{y}}^n\ln f_{w,b}\left(x^n\right)+\left(1-{\hat{y}}^n\right)\ln \left(1-f_{w,b}\left(x^n\right)\right)\right)\end{array}$$

函数中的y_pred即$f_{w,b}(x^n)$，Y_label即${\hat{y}}^n$

def _cross_entropy_loss(y_pred, Y_label):
    # This function computes the cross entropy.
    #
    # Arguements:
    #     y_pred: probabilistic predictions, float vector
    #     Y_label: ground truth labels, bool vector
    # Output:
    #     cross entropy, scalar
    cross_entropy = -np.dot(Y_label, np.log(y_pred)) - np.dot((1 - Y_label), np.log(1 - y_pred))
    return cross_entropy

梯度（Gradient）

$$\begin{array}{rl}\frac{\partial (-\ln L(w,b))}{\partial w_i}& =-\sum _n\left({\hat{y}}^n\frac{\partial \ln f_{w,b}\left(x^n\right)}{\partial w_i}+\left(1-{\hat{y}}^n\right)\frac{\partial \ln \left(1-f_{w,b}\left(x^n\right)\right)}{\partial w_i}\right)\end{array}$$
因为$$\begin{array}{rl}\frac{\partial \ln f_{w,b}\left(x^n\right)}{\partial w_i}& =\frac{\partial \ln f_{w,b}\left(x^n\right)}{\partial z}\cdot \frac{\partial z}{\partial w_i}\\ & =\frac{\partial \ln \sigma (z)}{\partial z}\cdot \frac{\partial z}{\partial w_i}\\ & =\frac{1}{\sigma (z)}\cdot \frac{\partial \sigma (z)}{\partial z}\cdot \frac{\partial z}{\partial w_i}\\ & =\frac{1}{\sigma (z)}\cdot \sigma (z)\cdot (1-\sigma (z))\cdot \frac{\sum w_i{x}_i^n+b}{\partial w_i}\\ & =(1-\sigma (z))\cdot x_i^n\\ & =(1-f_{w,b}\left(x^n\right))\cdot x_i^n\end{array}$$

$$\begin{array}{rl}\frac{\partial \ln \left(1-f_{w,b}\left(x^n\right)\right)}{\partial w_i}& =\frac{\partial \ln \left(1-f_{w,b}\left(x^n\right)\right)}{\partial z}\cdot \frac{\partial z}{\partial w_i}\\ & =\frac{\partial \ln (1-\sigma (z))}{\partial z}\cdot \frac{\partial z}{\partial w_i}\\ & =\frac{1}{1-\sigma (z)}\cdot (-1)\cdot \frac{\partial \sigma (z)}{\partial z}\cdot \frac{\partial z}{\partial w_i}\\ & =\frac{1}{1-\sigma (z)}\cdot (-1)\cdot \sigma (z)\cdot (1-\sigma (z))\cdot \frac{\sum w_i{x}_i^n+b}{\partial w_i}\\ & =-\sigma (z)\cdot x_i^n\\ & =-f_{w,b}(x^n)\cdot x_i^n\end{array}$$
所以
$$\begin{array}{rl}\frac{\partial (-\ln L(w,b))}{\partial w_i}& =-\sum _n\left({\hat{y}}^n\frac{\partial \ln f_{w,b}\left(x^n\right)}{\partial w_i}+\left(1-{\hat{y}}^n\right)\frac{\partial \ln \left(1-f_{w,b}\left(x^n\right)\right)}{\partial w_i}\right)\\ & =-\sum _n\left({\hat{y}}^n\cdot (1-f_{w,b}\left(x^n\right))\cdot x_i^n+\left(1-{\hat{y}}^n\right)\cdot (-f_{w,b}(x^n)\cdot x_i^n)\right)\\ & =-\sum _n\left({\hat{y}}^n-f_{w,b}\left(x^n\right)\right)x_i^n\end{array}$$
$\frac{\partial (-\ln L(w,b))}{\partial b}$与$\frac{\partial (-\ln L(w,b))}{\partial w_i}$类似，将$x_i^n$变为常数$1$即可：
$$\begin{array}{rl}\frac{\partial (-\ln L(w,b))}{\partial b}& =-\sum _n\left({\hat{y}}^n-f_{w,b}\left(x^n\right)\right)\end{array}$$
参数更新公式为：
$$w_i=w_i-\eta \frac{\partial (-\ln L(w,b))}{\partial w_i}=w_i-\eta \left(-\sum _n\left({\hat{y}}^n-f_{w,b}\left(x^n\right)\right)x_i^n\right)$$
因为后面用到了batch（小批次处理，一次同时训练多个数据$x^j$来更新参数），所以函数中输入的X和Y_lable都是1×N（N是批次大小）的一维数组，每一批次的w_grad是N个数据的梯度累加的和。

def _gradient(X, Y_label, w, b):
    # This function computes the gradient of cross entropy loss with respect to weight w and bias b.
    y_pred = _f(X, w, b)
    pred_error = Y_label - y_pred
    w_grad = -np.sum(pred_error * X.T, 1)
    b_grad = -np.sum(pred_error)
    return w_grad, b_grad

训练

使用小批次（mini-batch）的梯度下降法来训练。训练数据被分为许多小批次，针对每一个小批次，我们分别计算其梯度以及损失，并根据该批次来更新模型的参数。当一次循环（iteration）完成，也就是整个训练集的所有小批次都被使用过一次以后，我们将所有训练数据打散并且重新分成新的小批次，进行下一个循环，直到事先设定的循环数量（iteration）达成为止。

• GD（Gradient Descent）：就是没有利用Batch Size，用基于整个数据库得到梯度，梯度准确，但数据量大时，计算非常耗时，同时神经网络常是非凸的，网络最终可能收敛到初始点附近的局部最优点。

• SGD（Stochastic Gradient Descent）：就是Batch Size=1，每次计算一个样本，梯度不准确，所以学习率要降低。

• mini-batch SGD：就是选着合适Batch Size的SGD算法，mini-batch利用噪声梯度，一定程度上缓解了GD算法直接掉进初始点附近的局部最优值。同时梯度准确了，学习率要加大。
  ————————————————
  详情请见：神经网络中Batch Size的理解

这里权重$w$用了全0初始化，logistic regression 中可以用0初始化，原因如下：

逻辑回归的权重可以初始化为0的原因：
Logistic回归没有隐藏层。 如果将权重初始化为零，则Logistic回归中的第一个示例x将输出零，但Logistic回归的导数取决于不是零的输入x（因为没有隐藏层）。 因此，在第二次迭代（迭代发生在w和b值的更新中，即梯度下降）中，如果x不是常量向量，则权值遵循x的分布并且彼此不同。
————————————————
详情请见：逻辑回归和神经网络权重初始化为0的问题

# 初始化权重w和b，令它们都为0
w = np.zeros((data_dim,))	#[0,0,0,...,0]
b = np.zeros((1,))		 	#[0]

# 训练时的超参数
max_iter = 10
batch_size = 8
learning_rate = 0.2

# 保存每个iteration的loss和accuracy，以便后续画图
train_loss = []
dev_loss = []
train_acc = []
dev_acc = []

# 累计参数更新的次数
step = 1

# 迭代训练
for epoch in range(max_iter):
    # 在每个epoch开始时，随机打散训练数据
    X_train, Y_train = _shuffle(X_train, Y_train)
        
    # Mini-batch训练
    for idx in range(int(np.floor(train_size / batch_size))):
        X = X_train[idx*batch_size:(idx+1)*batch_size]
        Y = Y_train[idx*batch_size:(idx+1)*batch_size]

        # 计算梯度
        w_grad, b_grad = _gradient(X, Y, w, b)
            
        # 梯度下降法更新
        # 学习率随时间衰减
        w = w - learning_rate/np.sqrt(step) * w_grad
        b = b - learning_rate/np.sqrt(step) * b_grad

        step = step + 1
            
    # 计算训练集和验证集的loss和accuracy
    y_train_pred = _f(X_train, w, b)
    Y_train_pred = np.round(y_train_pred)
    train_acc.append(_accuracy(Y_train_pred, Y_train))
    train_loss.append(_cross_entropy_loss(y_train_pred, Y_train) / train_size)

    y_dev_pred = _f(X_dev, w, b)
    Y_dev_pred = np.round(y_dev_pred)
    dev_acc.append(_accuracy(Y_dev_pred, Y_dev))
    dev_loss.append(_cross_entropy_loss(y_dev_pred, Y_dev) / dev_size)

print('Training loss: {}'.format(train_loss[-1]))
print('Development loss: {}'.format(dev_loss[-1]))
print('Training accuracy: {}'.format(train_acc[-1]))
print('Development accuracy: {}'.format(dev_acc[-1]))

Out:
Training loss: 0.27186254652383707
Development loss: 0.29249918772983036
Training accuracy: 0.8839852549662093
Development accuracy: 0.8767047548838923

画出loss和accuracy的曲线

import matplotlib.pyplot as plt

# Loss曲线
plt.plot(train_loss)
plt.plot(dev_loss)
plt.title('Loss')
plt.legend(['train', 'dev'])
plt.savefig('loss.png')
plt.show()

# Accuracy曲线
plt.plot(train_acc)
plt.plot(dev_acc)
plt.title('Accuracy')
plt.legend(['train', 'dev'])
plt.savefig('acc.png')
plt.show()

测试（test）

测试集中共有27622个测试数据。预测测试集的标签，并保存在 output_logistic.csv 中。

保存格式为：第一行表头，总共两列，第一列是id，第二列是label：

# 预测测试集标签
predictions = _predict(X_test, w, b)
# 保存到output_logistic.csv
with open(output_fpath.format('logistic'), 'w') as f:
    f.write('id,label\n')
    for i, label in  enumerate(predictions):
        f.write('{},{}\n'.format(i, label))

# 输出最重要的特征和权重
# 对w的绝对值从大到小排序，输出对应的ID
ind = np.argsort(np.abs(w))[::-1]
with open(X_test_fpath) as f:
	# 读入表头（特征名）
    content = f.readline().strip('\n').split(',')
features = np.array(content)
for i in ind[0:10]:
    print(features[i], w[i])

Out:
Child <18 never marr not in subfamily -2.1583234422797783
 Unemployed full-time 1.142333082859196
 Philippines -1.0115599938948558
 Grandchild <18 never marr not in subfamily -0.9152892007169311
 1 0.8262256250590363
 Not in universe -0.7952475906445426
dividends from stocks -0.7026973895755972
 2 -0.6946992686020286
 High school graduate -0.6928617955365588
capital losses 0.6582145807985178

提交结果

在kaggle平台提交output_generative.csv，结果：

• Private Score=0.88914
• Public Score=0.88755

2.2 概率生成模型（Porbabilistic generative model）

数据预处理

训练集与测试集的处理方法跟 logistic regression 一模一样，然而因为 generative model 有可解析的最佳解，因此不必使用到验证集（development set）

# 把CSV文件转换为numpy
with open(X_train_fpath) as f:
    next(f)
    X_train = np.array([line.strip('\n').split(',')[1:] for line in f], dtype = float)
with open(Y_train_fpath) as f:
    next(f)
    Y_train = np.array([line.strip('\n').split(',')[1] for line in f], dtype = float)
with open(X_test_fpath) as f:
    next(f)
    X_test = np.array([line.strip('\n').split(',')[1:] for line in f], dtype = float)

# 标准化训练集和测试集
X_train, X_mean, X_std = _normalize(X_train, train = True)
X_test, _, _= _normalize(X_test, train = False, specified_column = None, X_mean = X_mean, X_std = X_std)

均值和协方差

在 generative model 中，我们需要分别计算两个类别内的数据的均值和协方差。

• 类别0（y=0）：年收入不超过50,000美元
  $${\mu }_0^{\ast }=\frac{1}{n_0}\sum _{i=0}^{n_0}{x}^i，{\Sigma }_0^{\ast }=\frac{1}{n_0}\sum _{i=0}^{n_0}\left(x^i-{\mu }_0^{\ast }\right){\left(x^i-{\mu }_0^{\ast }\right)}^T$$
• 类别1（y=1）：年收入超过50,000美元
  $${\mu }_1^{\ast }=\frac{1}{n_1}\sum _{i=0}^{n_1}{x}^i，{\Sigma }_1^{\ast }=\frac{1}{n_1}\sum _{i=0}^{n_1}\left(x^i-{\mu }_1^{\ast }\right){\left(x^i-{\mu }_1^{\ast }\right)}^T$$
  其中，$n_0$是类别0的个数，$n_1$是类别1的个数。

最终，模型共享的协方差矩阵为所有协方差的加权平均值：${\Sigma }^{\ast }=\frac{n_0}{n_0+n_1}{\Sigma }_0^{\ast }+\frac{n_1}{n_0+n_1}{\Sigma }_1^{\ast }$

这段代码运行时间较长。

# 分别计算类别0和类别1的均值
X_train_0 = np.array([x for x, y in zip(X_train, Y_train) if y == 0]) 
X_train_1 = np.array([x for x, y in zip(X_train, Y_train) if y == 1])

mean_0 = np.mean(X_train_0, axis = 0)
mean_1 = np.mean(X_train_1, axis = 0)  

# 分别计算类别0和类别1的协方差
cov_0 = np.zeros((data_dim, data_dim))
cov_1 = np.zeros((data_dim, data_dim))

for x in X_train_0:
    cov_0 += np.dot(np.transpose([x - mean_0]), [x - mean_0]) / X_train_0.shape[0]
for x in X_train_1:
    cov_1 += np.dot(np.transpose([x - mean_1]), [x - mean_1]) / X_train_1.shape[0]

# 共享协方差 = 独立的协方差的加权求和
cov = (cov_0 * X_train_0.shape[0] + cov_1 * X_train_1.shape[0]) / (X_train_0.shape[0] + X_train_1.shape[0])

计算权重和偏差

权重矩阵与偏差向量可以直接被计算出来，详情可见视频P10 Classification：
$$w^T={\left({\mu }^0-{\mu }^1\right)}^T{\Sigma }^{-1}$$

$$b=-\frac{1}{2}{\left({\mu }^0\right)}^T{\Sigma }^{-1}{\mu }^0+\frac{1}{2}{\left({\mu }^1\right)}^T{\Sigma }^{-1}{\mu }^1+\ln \frac{n_0}{n_1}$$

# 计算协方差矩阵的逆
# 协方差矩阵可能是奇异矩阵, 直接使用np.linalg.inv() 可能会产生错误
# 通过SVD矩阵分解，可以快速准确地获得方差矩阵的逆
u, s, v = np.linalg.svd(cov, full_matrices=False)
inv = np.matmul(v.T * 1 / s, u.T)

# 计算w和b
w = np.dot(inv, mean_0 - mean_1)
b =  (-0.5) * np.dot(mean_0, np.dot(inv, mean_0)) + 0.5 * np.dot(mean_1, np.dot(inv, mean_1))\
    + np.log(float(X_train_0.shape[0]) / X_train_1.shape[0]) 

# 计算训练集上的准确率
Y_train_pred = 1 - _predict(X_train, w, b)
print('Training accuracy: {}'.format(_accuracy(Y_train_pred, Y_train)))

Out:
Training accuracy: 0.8725302270716603

测试

预测测试集的标签，并保存在 output_generative.csv 中。

# 预测测试集的label
predictions = 1 - _predict(X_test, w, b)
with open(output_fpath.format('generative'), 'w') as f:
    f.write('id,label\n')
    for i, label in  enumerate(predictions):
        f.write('{},{}\n'.format(i, label))

# 输出最重要的9个特征
ind = np.argsort(np.abs(w))[::-1]
with open(X_test_fpath) as f:
    content = f.readline().strip('\n').split(',')
features = np.array(content)
for i in ind[0:10]:
    print(features[i], w[i])

Out:
Retail trade 8.3359375
 Not in universe -6.703125
 34 -6.33203125
 37 -5.80859375
 Different county same state -5.65625
 Other service -5.42578125
 Abroad 4.625
 Finance insurance and real estate 4.0
 Same county 4.0
 Other Rel 18+ never marr RP of subfamily 3.9375

提交结果

在kaggle平台提交output_generative.csv，结果：

• Private Score=0.87690
• Public Score=0.88067

2.3 总结

两种方法在kaggle上的评分不同：

方法	Private Score	Public Score
Logistic Regression	0.88914	0.88755
Generative Model	0.87690	0.88067

两种方法虽然都是计算权重$w$和偏差$b$，但是最终获得的$w$和$b$是不同的，这和视频上李宏毅所说的一致。

3 修改代码

首先，将学习率的衰减改成了adagrad。其次，加了一个特征的二次项（见函数_add_feature(X)），提升也比较显著。

想通过其它方法得到更好的结果，可以继续修改学习率、batch size等等，提升效果在0.01左右上下浮动，然而博主缺乏调参经验，花的时间太多（调参调了两天），目前结果还算看得过去，就暂时贴上自己的代码。

import numpy as np

np.random.seed(0)
X_train_fpath = './data/X_train'
Y_train_fpath = './data/Y_train'
X_test_fpath = './data/X_test'
output_fpath = './output_{}.csv'

# 把csv文件转换成numpy的数组
with open(X_train_fpath) as f:
    next(f)
    X_train = np.array([line.strip('\n').split(',')[1:] for line in f], dtype = float)
with open(Y_train_fpath) as f:
    next(f)
    Y_train = np.array([line.strip('\n').split(',')[1] for line in f], dtype = float)
with open(X_test_fpath) as f:
    next(f)
    X_test = np.array([line.strip('\n').split(',')[1:] for line in f], dtype = float)

def _normalize(X, train=True, specified_column=None, X_mean=None, X_std=None):
    if specified_column == None:
        specified_column = np.arange(X.shape[1])
    if train:
        X_mean = np.mean(X[:, specified_column], 0).reshape(1, -1)
        X_std = np.std(X[:, specified_column], 0).reshape(1, -1)

    X[:, specified_column] = (X[:, specified_column] - X_mean) / (X_std + 1e-8)  # 1e-8防止除零

    return X, X_mean, X_std

def _add_feature(X):
    X_2 = np.power(X,2)
    X = np.concatenate([X,X_2], axis=1)
    return X

# 引入二次项
X_train = _add_feature(X_train)
X_test = _add_feature(X_test)

# 标准化训练数据和测试数据
X_train, X_mean, X_std = _normalize(X_train, train=True)
X_test, _, _ = _normalize(X_test, train=False, specified_column=None, X_mean=X_mean, X_std=X_std)

def _train_dev_split(X, Y, dev_ratio=0.25):
    # This function spilts data into training set and development set.
    train_size = int(len(X) * (1 - dev_ratio))
    return X[:train_size], Y[:train_size], X[train_size:], Y[train_size:]

# 把数据分成训练集和验证集
dev_ratio = 0.1
X_train, Y_train, X_dev, Y_dev = _train_dev_split(X_train, Y_train, dev_ratio=dev_ratio)

train_size = X_train.shape[0]
dev_size = X_dev.shape[0]
test_size = X_test.shape[0]
data_dim = X_train.shape[1]
print('Size of training set: {}'.format(train_size))
print('Size of development set: {}'.format(dev_size))
print('Size of testing set: {}'.format(test_size))
print('Dimension of data: {}'.format(data_dim))

def _shuffle(X, Y):
    # This function shuffles two equal-length list/array, X and Y, together.
    randomize = np.arange(len(X))
    np.random.shuffle(randomize)
    return (X[randomize], Y[randomize])

def _sigmoid(z):
    # Sigmoid function can be used to calculate probability.
    # To avoid overflow, minimum/maximum output value is set.
    return np.clip(1 / (1.0 + np.exp(-z)), 1e-8, 1 - (1e-8))

def _f(X, w, b):
    # This is the logistic regression function, parameterized by w and b
    #
    # Arguements:
    #     X: input data, shape = [batch_size, data_dimension]
    #     w: weight vector, shape = [data_dimension, ]
    #     b: bias, scalar
    # Output:
    #     predicted probability of each row of X being positively labeled, shape = [batch_size, ]
    return _sigmoid(np.matmul(X, w) + b)

def _predict(X, w, b):
    # This function returns a truth value prediction for each row of X
    # by rounding the result of logistic regression function.
    return np.round(_f(X, w, b)).astype(np.int)

def _accuracy(Y_pred, Y_label):
    # This function calculates prediction accuracy
    acc = 1 - np.mean(np.abs(Y_pred - Y_label))
    return acc

def _cross_entropy_loss(y_pred, Y_label):
    # This function computes the cross entropy.
    #
    # Arguements:
    #     y_pred: probabilistic predictions, float vector
    #     Y_label: ground truth labels, bool vector
    # Output:
    #     cross entropy, scalar
    cross_entropy = -np.dot(Y_label, np.log(y_pred)) - np.dot((1 - Y_label), np.log(1 - y_pred))
    return cross_entropy

def _gradient(X, Y_label, w, b):
    # This function computes the gradient of cross entropy loss with respect to weight w and bias b.
    y_pred = _f(X, w, b)
    pred_error = Y_label - y_pred
    w_grad = -np.sum(pred_error * X.T, 1)
    b_grad = -np.sum(pred_error)
    return w_grad, b_grad

# 初始化权重w和b，令它们都为0
w = np.zeros((data_dim,))  # [0,0,0,...,0]
b = np.zeros((1,))  # [0]

# 训练时的超参数
max_iter = 272
batch_size = 128
learning_rate = 0.1

# 保存每个iteration的loss和accuracy，以便后续画图
train_loss = []
dev_loss = []
train_acc = []
dev_acc = []

# adagrad所需的累加和
adagrad_w = 0
adagrad_b = 0
# 防止adagrad除零
eps = 1e-8

# 迭代训练
for epoch in range(max_iter):
    # 在每个epoch开始时，随机打散训练数据
    X_train, Y_train = _shuffle(X_train, Y_train)

    # Mini-batch训练
    for idx in range(int(np.floor(train_size / batch_size))):
        X = X_train[idx * batch_size:(idx + 1) * batch_size]
        Y = Y_train[idx * batch_size:(idx + 1) * batch_size]

        # 计算梯度
        w_grad, b_grad = _gradient(X, Y, w, b)
        adagrad_w += w_grad**2
        adagrad_b += b_grad**2

        # 梯度下降法adagrad更新w和b
        w = w - learning_rate / (np.sqrt(adagrad_w + eps)) * w_grad
        b = b - learning_rate / (np.sqrt(adagrad_b + eps)) * b_grad

    # 计算训练集和验证集的loss和accuracy
    y_train_pred = _f(X_train, w, b)
    Y_train_pred = np.round(y_train_pred)
    train_acc.append(_accuracy(Y_train_pred, Y_train))
    train_loss.append(_cross_entropy_loss(y_train_pred, Y_train) / train_size)

    y_dev_pred = _f(X_dev, w, b)
    Y_dev_pred = np.round(y_dev_pred)
    dev_acc.append(_accuracy(Y_dev_pred, Y_dev))
    dev_loss.append(_cross_entropy_loss(y_dev_pred, Y_dev) / dev_size)

print('Training loss: {}'.format(train_loss[-1]))
print('Development loss: {}'.format(dev_loss[-1]))
print('Training accuracy: {}'.format(train_acc[-1]))
print('Development accuracy: {}'.format(dev_acc[-1]))

# 绘制曲线
import matplotlib.pyplot as plt

# Loss曲线
plt.plot(train_loss)
plt.plot(dev_loss)
plt.title('Loss')
plt.legend(['train', 'dev'])
plt.savefig('loss.png')
plt.show()

# Accuracy曲线
plt.plot(train_acc)
plt.plot(dev_acc)
plt.title('Accuracy')
plt.legend(['train', 'dev'])
plt.savefig('acc.png')
plt.show()

# 预测测试集标签
predictions = _predict(X_test, w, b)
# 保存到output_logistic.csv
with open(output_fpath.format('logistic'), 'w') as f:
    f.write('id,label\n')
    for i, label in enumerate(predictions):
        f.write('{},{}\n'.format(i, label))

结果如下：

Private Score：0.89124
Public Score：0.89095