Tensorflow2.*教程之对预处理的IMDB电影评论数据集进行文本分类(3)
Keras 机器学习基础知识:
- 对服装图像进行分类
- 使用Tensorflow Hub对未处理的电影评论数据集IMDB进行分类
- 后续关于tensorflow 2.0文章继续更新...........
现在是凌晨五点多了,睡不着,来更新一篇文章。今天文章的题目是使用tensorflow2.0对预处理的IMDB数据集进行分类,在前面的文章Tensorflow2.*教程之使用 Keras 和 Tensorflow Hub 对电影评论进行文本分类(2)中我们使用的IMDB数据是纯文本数据,本次使用的数据是预处理的数据,也就是说官方已经对每个句子进行了word2id处理。现在开始我们今天的正题。
IMDB数据集介绍
网络电影数据库(Internet Movie Database)的 IMDB 数据集(IMDB dataset),其包含 50,000 条影评文本。从该数据集切割出的25,000条评论用作训练,另外 25,000 条用作测试。该数据集类别均衡。
引入必要的Python库
from __future__ import absolute_import, division, print_function, unicode_literals
import tensorflow as tf
from tensorflow import keras
import numpy as np
print(tf.__version__)下载 IMDB 数据集
IMDB 数据集已经打包在 Tensorflow 中。该数据集已经经过预处理,评论(单词序列)已经被转换为整数序列,其中每个整数表示字典中的特定单词。
以下代码将下载 IMDB 数据集到您的机器上(如果您已经下载过将从缓存中复制)。
参数 num_words=10000 保留了训练数据中最常出现的 10000 个单词。为了保持数据规模的可管理性,低频词将被丢弃。
imdb = keras.datasets.imdb
(train_data, train_labels), (test_data, test_labels) = imdb.load_data(num_words=10000)IMDB数据集介绍
该数据集是经过预处理的:每个样本都是一个表示影评中词汇的整数数组。每个标签都是一个值为 0 或 1 的整数值,其中 0 代表消极评论,1 代表积极评论。
print("Training entries: {}, labels: {}".format(len(train_data), len(train_labels)))Training entries: 25000, labels: 25000
评论文本被转换为整数值,其中每个整数代表词典中的一个单词。首条评论是这样的:
print(train_data[0])[1, 14, 22, 16, 43, 530, 973, 1622, 1385, 65, 458, 4468, 66, 3941, 4, 173, 36, 256, 5, 25, 100, 43, 838, 112, 50, 670, 2, 9, 35, 480, 284, 5, 150, 4, 172, 112, 167, 2, 336, 385, 39, 4, 172, 4536, 1111, 17, 546, 38, 13, 447, 4, 192, 50, 16, 6, 147, 2025, 19, 14, 22, 4, 1920, 4613, 469, 4, 22, 71, 87, 12, 16, 43, 530, 38, 76, 15, 13, 1247, 4, 22, 17, 515, 17, 12, 16, 626, 18, 2, 5, 62, 386, 12, 8, 316, 8, 106, 5, 4, 2223, 5244, 16, 480, 66, 3785, 33, 4, 130, 12, 16, 38, 619, 5, 25, 124, 51, 36, 135, 48, 25, 1415, 33, 6, 22, 12, 215, 28, 77, 52, 5, 14, 407, 16, 82, 2, 8, 4, 107, 117, 5952, 15, 256, 4, 2, 7, 3766, 5, 723, 36, 71, 43, 530, 476, 26, 400, 317, 46, 7, 4, 2, 1029, 13, 104, 88, 4, 381, 15, 297, 98, 32, 2071, 56, 26, 141, 6, 194, 7486, 18, 4, 226, 22, 21, 134, 476, 26, 480, 5, 144, 30, 5535, 18, 51, 36, 28, 224, 92, 25, 104, 4, 226, 65, 16, 38, 1334, 88, 12, 16, 283, 5, 16, 4472, 113, 103, 32, 15, 16, 5345, 19, 178, 32]
电影评论可能具有不同的长度。以下代码显示了第一条和第二条评论的中单词数量。由于神经网络的输入必须是统一的长度,我们稍后需要解决这个问题。
len(train_data[0]), len(train_data[1])(218, 189)
将整数转换回单词
# 一个映射单词到整数索引的词典
word_index = imdb.get_word_index()
# 保留第一个索引
word_index = {k:(v+3) for k,v in word_index.items()}
word_index[""] = 0
word_index[""] = 1
word_index[""] = 2 # unknown
word_index[""] = 3
reverse_word_index = dict([(value, key) for (key, value) in word_index.items()])
def decode_review(text):
return ' '.join([reverse_word_index.get(i, '?') for i in text]) 现在我们可以使用 decode_review 函数来显示首条评论的文本:
decode_review(train_data[0])"this film was just brilliant casting location scenery story direction everyone's really suited the part they played and you could just imagine being there robert is an amazing actor and now the same being director father came from the same scottish island as myself so i loved the fact there was a real connection with this film the witty remarks throughout the film were great it was just brilliant so much that i bought the film as soon as it was released for and would recommend it to everyone to watch and the fly fishing was amazing really cried at the end it was so sad and you know what they say if you cry at a film it must have been good and this definitely was also to the two little boy's that played the of norman and paul they were just brilliant children are often left out of the list i think because the stars that play them all grown up are such a big profile for the whole film but these children are amazing and should be praised for what they have done don't you think the whole story was so lovely because it was true and was someone's life after all that was shared with us all"
将训练和测试数据处理成相同长度
影评——由于影评数据本身长度不一,为了送入网络,我们首先要将其变为相同的长度,有如下两种方法:
-
将数组转换为表示单词出现与否的由 0 和 1 组成的向量,类似于 one-hot 编码。例如,序列[3, 5]将转换为一个 10,000 维的向量,该向量除了索引为 3 和 5 的位置是 1 以外,其他都为 0。然后,将其作为网络的首层——一个可以处理浮点型向量数据的稠密层。不过,这种方法需要大量的内存,需要一个大小为
num_words * num_reviews的矩阵。 -
或者,我们可以填充数组来保证输入数据具有相同的长度,然后创建一个大小为
max_length * num_reviews的整型张量。我们可以使用能够处理此形状数据的嵌入层作为网络中的第一层。
本次实验,我们使用第二种方法,我们使用 pad_sequences 函数来使长度标准化:
train_data = keras.preprocessing.sequence.pad_sequences(train_data,
value=word_index[""],
padding='post',
maxlen=256)
test_data = keras.preprocessing.sequence.pad_sequences(test_data,
value=word_index[""],
padding='post',
maxlen=256) 现在让我们看下样本的长度:
len(train_data[0]), len(train_data[1])构建模型
神经网络由堆叠的层来构建,这需要从两个主要方面来进行体系结构决策:
- 模型里有多少层?
- 每个层里有多少隐层单元(hidden units)?
在此样本中,输入数据包含一个单词索引的数组。要预测的标签为 0 或 1。让我们来为该问题构建一个模型:
# 输入形状是用于电影评论的词汇数目(10,000 词)
vocab_size = 10000
model = keras.Sequential()
model.add(keras.layers.Embedding(vocab_size, 16))
model.add(keras.layers.GlobalAveragePooling1D())
model.add(keras.layers.Dense(16, activation='relu'))
model.add(keras.layers.Dense(1, activation='sigmoid'))
model.summary()Model: "sequential" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= embedding (Embedding) (None, None, 16) 160000 _________________________________________________________________ global_average_pooling1d (Gl (None, 16) 0 _________________________________________________________________ dense (Dense) (None, 16) 272 _________________________________________________________________ dense_1 (Dense) (None, 1) 17 ================================================================= Total params: 160,289 Trainable params: 160,289 Non-trainable params: 0
层按顺序堆叠以构建分类器:
- 第一层是
嵌入(Embedding)层。该层采用整数编码的词汇表,并查找每个词索引的嵌入向量(embedding vector)。这些向量是通过模型训练学习到的。向量向输出数组增加了一个维度。得到的维度为:(batch, sequence, embedding)。 - 接下来,
GlobalAveragePooling1D将通过对序列维度求平均值来为每个样本返回一个定长输出向量。这允许模型以尽可能最简单的方式处理变长输入。 - 该定长输出向量通过一个有 16 个隐层单元的全连接(
Dense)层传输。 - 最后一层与单个输出结点密集连接。使用
Sigmoid激活函数,其函数值为介于 0 与 1 之间的浮点数,表示概率或置信度。
损失函数与优化器
一个模型需要损失函数和优化器来进行训练。由于这是一个二分类问题且模型输出概率值(一个使用 sigmoid 激活函数的单一单元层),我们将使用 binary_crossentropy 损失函数。
这不是损失函数的唯一选择,例如,您可以选择 mean_squared_error 。但是,一般来说 binary_crossentropy 更适合处理概率——它能够度量概率分布之间的“距离”,或者在我们的示例中,指的是度量 ground-truth 分布与预测值之间的“距离”。
稍后,当我们研究回归问题(例如,预测房价)时,我们将介绍如何使用另一种叫做均方误差的损失函数。
现在,配置模型来使用优化器和损失函数:
model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy'])创建一个验证集
在训练时,我们想要检查模型在未见过的数据上的准确率(accuracy)。通过从原始训练数据中分离 10,000 个样本来创建一个验证集。(为什么现在不使用测试集?我们的目标是只使用训练数据来开发和调整模型,然后只使用一次测试数据来评估准确率(accuracy))。
x_val = train_data[:10000]
partial_x_train = train_data[10000:]
y_val = train_labels[:10000]
partial_y_train = train_labels[10000:]训练模型
以 512 个样本的 mini-batch 大小迭代 40 个 epoch 来训练模型。这是指对 x_train 和 y_train 张量中所有样本的的 40 次迭代。在训练过程中,监测来自验证集的 10,000 个样本上的损失值(loss)和准确率(accuracy)
history = model.fit(partial_x_train,
partial_y_train,
epochs=40,
batch_size=512,
validation_data=(x_val, y_val),
verbose=1)Train on 15000 samples, validate on 10000 samples Epoch 1/40 15000/15000 [==============================] - 1s 88us/sample - loss: 0.6924 - accuracy: 0.6045 - val_loss: 0.6910 - val_accuracy: 0.6819 Epoch 2/40 15000/15000 [==============================] - 0s 22us/sample - loss: 0.6885 - accuracy: 0.6392 - val_loss: 0.6856 - val_accuracy: 0.7129 Epoch 3/40 15000/15000 [==============================] - 0s 22us/sample - loss: 0.6798 - accuracy: 0.7371 - val_loss: 0.6747 - val_accuracy: 0.7141 Epoch 4/40 15000/15000 [==============================] - 0s 22us/sample - loss: 0.6629 - accuracy: 0.7648 - val_loss: 0.6539 - val_accuracy: 0.7597 Epoch 5/40 15000/15000 [==============================] - 0s 21us/sample - loss: 0.6356 - accuracy: 0.7860 - val_loss: 0.6239 - val_accuracy: 0.7783 Epoch 6/40 15000/15000 [==============================] - 0s 22us/sample - loss: 0.5975 - accuracy: 0.8036 - val_loss: 0.5849 - val_accuracy: 0.7931 Epoch 7/40 15000/15000 [==============================] - 0s 22us/sample - loss: 0.5525 - accuracy: 0.8195 - val_loss: 0.5421 - val_accuracy: 0.8076 Epoch 8/40 15000/15000 [==============================] - 0s 22us/sample - loss: 0.5025 - accuracy: 0.8357 - val_loss: 0.4961 - val_accuracy: 0.8245 Epoch 9/40 15000/15000 [==============================] - 0s 22us/sample - loss: 0.4541 - accuracy: 0.8537 - val_loss: 0.4555 - val_accuracy: 0.8392 Epoch 10/40 15000/15000 [==============================] - 0s 22us/sample - loss: 0.4114 - accuracy: 0.8672 - val_loss: 0.4211 - val_accuracy: 0.8469 Epoch 11/40 15000/15000 [==============================] - 0s 22us/sample - loss: 0.3753 - accuracy: 0.8775 - val_loss: 0.3938 - val_accuracy: 0.8531 Epoch 12/40 15000/15000 [==============================] - 0s 22us/sample - loss: 0.3451 - accuracy: 0.8859 - val_loss: 0.3713 - val_accuracy: 0.8600 Epoch 13/40 15000/15000 [==============================] - 0s 21us/sample - loss: 0.3201 - accuracy: 0.8924 - val_loss: 0.3540 - val_accuracy: 0.8665 Epoch 14/40 15000/15000 [==============================] - 0s 22us/sample - loss: 0.2990 - accuracy: 0.8983 - val_loss: 0.3397 - val_accuracy: 0.8712 Epoch 15/40 15000/15000 [==============================] - 0s 23us/sample - loss: 0.2809 - accuracy: 0.9037 - val_loss: 0.3290 - val_accuracy: 0.8735 Epoch 16/40 15000/15000 [==============================] - 0s 22us/sample - loss: 0.2649 - accuracy: 0.9095 - val_loss: 0.3197 - val_accuracy: 0.8766 Epoch 17/40 15000/15000 [==============================] - 0s 22us/sample - loss: 0.2508 - accuracy: 0.9131 - val_loss: 0.3121 - val_accuracy: 0.8792 Epoch 18/40 15000/15000 [==============================] - 0s 22us/sample - loss: 0.2379 - accuracy: 0.9183 - val_loss: 0.3063 - val_accuracy: 0.8797 Epoch 19/40 15000/15000 [==============================] - 0s 22us/sample - loss: 0.2262 - accuracy: 0.9216 - val_loss: 0.3013 - val_accuracy: 0.8806 Epoch 20/40 15000/15000 [==============================] - 0s 21us/sample - loss: 0.2156 - accuracy: 0.9261 - val_loss: 0.2972 - val_accuracy: 0.8828 Epoch 21/40 15000/15000 [==============================] - 0s 22us/sample - loss: 0.2061 - accuracy: 0.9292 - val_loss: 0.2939 - val_accuracy: 0.8827 Epoch 22/40 15000/15000 [==============================] - 0s 22us/sample - loss: 0.1966 - accuracy: 0.9329 - val_loss: 0.2918 - val_accuracy: 0.8833 Epoch 23/40 15000/15000 [==============================] - 0s 21us/sample - loss: 0.1881 - accuracy: 0.9368 - val_loss: 0.2892 - val_accuracy: 0.8837 Epoch 24/40 15000/15000 [==============================] - 0s 22us/sample - loss: 0.1802 - accuracy: 0.9408 - val_loss: 0.2884 - val_accuracy: 0.8841 Epoch 25/40 15000/15000 [==============================] - 0s 21us/sample - loss: 0.1725 - accuracy: 0.9436 - val_loss: 0.2871 - val_accuracy: 0.8845 Epoch 26/40 15000/15000 [==============================] - 0s 22us/sample - loss: 0.1656 - accuracy: 0.9468 - val_loss: 0.2863 - val_accuracy: 0.8856 Epoch 27/40 15000/15000 [==============================] - 0s 22us/sample - loss: 0.1592 - accuracy: 0.9494 - val_loss: 0.2863 - val_accuracy: 0.8862 Epoch 28/40 15000/15000 [==============================] - 0s 21us/sample - loss: 0.1529 - accuracy: 0.9516 - val_loss: 0.2868 - val_accuracy: 0.8851 Epoch 29/40 15000/15000 [==============================] - 0s 21us/sample - loss: 0.1465 - accuracy: 0.9555 - val_loss: 0.2871 - val_accuracy: 0.8860 Epoch 30/40 15000/15000 [==============================] - 0s 22us/sample - loss: 0.1410 - accuracy: 0.9568 - val_loss: 0.2882 - val_accuracy: 0.8858 Epoch 31/40 15000/15000 [==============================] - 0s 22us/sample - loss: 0.1354 - accuracy: 0.9591 - val_loss: 0.2896 - val_accuracy: 0.8858 Epoch 32/40 15000/15000 [==============================] - 0s 24us/sample - loss: 0.1303 - accuracy: 0.9618 - val_loss: 0.2906 - val_accuracy: 0.8865 Epoch 33/40 15000/15000 [==============================] - 0s 24us/sample - loss: 0.1251 - accuracy: 0.9639 - val_loss: 0.2923 - val_accuracy: 0.8858 Epoch 34/40 15000/15000 [==============================] - 0s 23us/sample - loss: 0.1206 - accuracy: 0.9658 - val_loss: 0.2941 - val_accuracy: 0.8858 Epoch 35/40 15000/15000 [==============================] - 0s 23us/sample - loss: 0.1164 - accuracy: 0.9668 - val_loss: 0.2972 - val_accuracy: 0.8849 Epoch 36/40 15000/15000 [==============================] - 0s 24us/sample - loss: 0.1116 - accuracy: 0.9683 - val_loss: 0.2992 - val_accuracy: 0.8845 Epoch 37/40 15000/15000 [==============================] - 0s 23us/sample - loss: 0.1075 - accuracy: 0.9709 - val_loss: 0.3010 - val_accuracy: 0.8842 Epoch 38/40 15000/15000 [==============================] - 0s 24us/sample - loss: 0.1036 - accuracy: 0.9715 - val_loss: 0.3067 - val_accuracy: 0.8807 Epoch 39/40 15000/15000 [==============================] - 0s 24us/sample - loss: 0.0996 - accuracy: 0.9724 - val_loss: 0.3068 - val_accuracy: 0.8830 Epoch 40/40 15000/15000 [==============================] - 0s 24us/sample - loss: 0.0956 - accuracy: 0.9749 - val_loss: 0.3109 - val_accuracy: 0.8823
模型评估
我们来看一下模型的性能如何。将返回两个值。损失值(loss)(一个表示误差的数字,值越低越好)与准确率(accuracy)。
results = model.evaluate(test_data, test_labels, verbose=2)
print(results)25000/1 - 2s - loss: 0.3454 - accuracy: 0.8732 [0.32927662477493286, 0.8732]
创建一个准确率(accuracy)和损失值(loss)随时间变化的图表
model.fit() 返回一个 History 对象,该对象包含一个字典,其中包含训练阶段所发生的一切事件:
history_dict = history.history
history_dict.keys()dict_keys(['loss', 'accuracy', 'val_loss', 'val_accuracy'])
有四个条目:在训练和验证期间,每个条目对应一个监控指标。我们可以使用这些条目来绘制训练与验证过程的损失值(loss)和准确率(accuracy),以便进行比较。
import matplotlib.pyplot as plt
acc = history_dict['accuracy']
val_acc = history_dict['val_accuracy']
loss = history_dict['loss']
val_loss = history_dict['val_loss']
epochs = range(1, len(acc) + 1)
# “bo”代表 "蓝点"
plt.plot(epochs, loss, 'bo', label='Training loss')
# b代表“蓝色实线”
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()plt.clf() # 清除数字
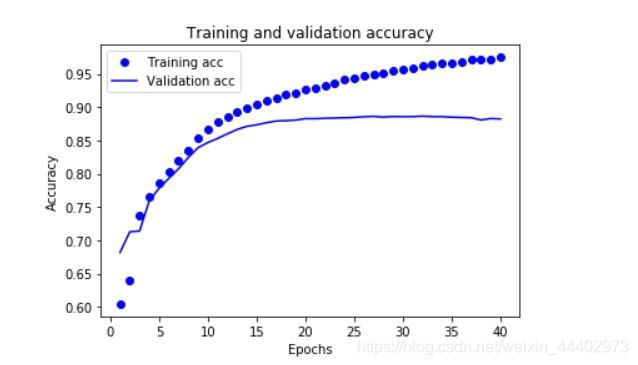
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()在上图中,点代表训练损失值(loss)与准确率(accuracy),实线代表验证损失值(loss)与准确率(accuracy)
注意训练损失值随每一个 epoch 下降而训练准确率(accuracy)随每一个 epoch 上升。这在使用梯度下降优化时是可预期的——理应在每次迭代中最小化期望值。
验证过程的损失值(loss)与准确率(accuracy)的情况却并非如此——它们似乎在 20 个 epoch 后达到峰值。这是过拟合的一个实例:模型在训练数据上的表现比在以前从未见过的数据上的表现要更好。在此之后,模型过度优化并学习特定于训练数据的表示,而不能够泛化到测试数据。
对于这种特殊情况,我们可以通过在 20 个左右的 epoch 后停止训练来避免过拟合。