四足机器人足端轨迹规划那点事(文献解读)
上述的足端轨迹规划材料来源于这篇文献
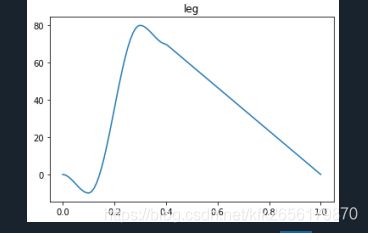
但是经过阅读发现文章中出现了问题,不知是自己理解错了还是本文章本身就有错误,错误如下
经过修改后通过python画图可实现
以下为python代码部分:
# -*- coding: utf-8 -*-
"""
Created on Tue Apr 21 17:20:06 2020
@author: kfk
"""
import matplotlib.pyplot as plt
import math
import numpy as np
S0=10#身体质心位移距离
S=60.0#跨步距离,步幅
T=1#一条腿的运动时间周期
T1=0.1#在ME花费的时间
T2=0.2#在EF花费的时间
x1=-10.0#假设E点的位置(-10,Z)
x2=-5.0#设EM中间点(x2=0.5*x1)
t1=T1/2#假设运动到x2点花费的时间恰好为T1的一半(方便求解)
Tsw=0.4#机器人处于摆动相的时间也是占空比(假设一条腿的运动时间周期为T=1s这占空比beta=0.6s则处于摆动相的时间为0.4s)
t = np.linspace(0,1,100)#
'''
曲线ME X位移随时间的变化
'''
b13=np.round((t1**2*x1-T1**2*x2)/(S*((T1**3)*(t1**2)-(T1**2)*(t1**3))), 2)
b12=np.round((x1/S-b13*T1**3)/T1**2,2)
X1=S*(b12*t**2+b13*t**3)
'''
曲线EF X位移随时间的变化
'''
a=(S+S0)/2-x1#椭圆长轴
X2=-a*np.cos((t-T1)*np.pi/T2)+(S+S0)/2
'''
曲线FN X位移随时间的变化
'''
t2=T1+T2
ka=Tsw-t2
t3=1.5*T1+T2
kb=Tsw-t3
fa=(S+S0-x1)/S
fb=(S+S0-x2)/S
fc=(S+S0)/S
b20=fc
b23=np.round(((fa-b20)*kb**2-(fb-b20)*ka**2)/(ka**3*kb**2-kb**3*ka**2),2)
b22=np.round((fa-b20-b23*ka**3)/ka**2,2)
X3=S*(b20+b22*(Tsw-t)**2+b23*(Tsw-t)**3)
'''
直线 X位移随时间的变化
'''
b31=(S+S0)/(Tsw-T)
b32=S+S0-b31*Tsw
X4=b31*t+b32
cond = [True if (i>0.1 and i<0.3) else False for i in t]
cond1 = [True if (i>0.3 and i<0.4) else False for i in t]
Y0=X1*(t<0.1)+X2*cond+X3*cond1+X4*(t>=0.4)
plt.title("leg")
plt.plot(t, Y0)
plt.show()
H=30
Z1=10
Z2=0.5*Z1
b=H-Z1
a13=(Z1*t1**2-Z2*T1**2)/H*(T1**3*t1**2-t2**3*T1**2)
a12=(Z1/H-a13*T1**3)/T1**2
X5=H*(a12*t**2+a13*t**3)
X6=b*np.sin((t-T1)*np.pi/T2)+Z1
a23=(kb**2*Z1-ka**2*Z2)/H*(ka**3*kb**2-ka**2*kb**3)
a22=(Z1/H-a23*ka**3)/ka**2
print(a22,a23)
X7=H*(a22*(Tsw-t)**2+a23*(Tsw-t)**3)
X8=0
Y1=X5*(t<0.1)+X6*cond+X7*cond1+X8*(t>0.4)
plt.title("leg")
plt.plot(t, Y1)
plt.show()
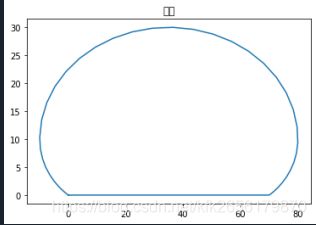
plt.title("leg")
plt.plot(Y0, Y1)
plt.show()