【关于四足机器人那些事】零力矩点（zmp）

根据零力矩点理论分析机器人行进过程的稳定条件，利用稳定裕度的概念，在支撑多边形中求取最优稳定点来规划零力矩点．可以为避免 walk步态中频繁调整躯干姿态导致的能耗和行进速度损失[1]

此外，“零力矩点”是判定仿人机器人动态稳定运动的重要指标，ZMP落在四足机器人支撑多边形的范围里面，则机器人可以稳定的行走。

前言

以下内容均为论文《基于零力矩点的四足机器人非平坦 地形下步态规划与控制》的部分解读，想要跟深入了解请查看原文

由于以下内容涉及到之前介绍过的相关内容，因此在您继续阅读之前，请确保已经对以下文章的内容有一定了解：

腿部运动学建模（三维）

腿部运动学建模（二维）

空间描述与变换

一、支撑多边形

在了解零力矩点之前，需要先了解另外一个概念：支撑多边形。它指的是四足机器人足底与地面之间所有接触点所构成的多边形区域。ZMP点是位于支撑多边形所组成的平面中的，因此，要求ZMP点，就需要先求出支撑多边形，我们可以用各个接触点的坐标来表征该多边形。

由于walk步态在低速行走时具有稳定性好、对越障和不平地形适应性强等优势，本文将主要对walk步态下的zmp进行研究。

要确定支撑多边形各个顶点的坐标值。因此需要先对四足机器人进行建模．

坐标系

对我们的机器人建模，第一步要做的肯定是建立坐标系啦，有了坐标系，我们才能知道所需要点的相对位置。我们先按以下原则确定坐标轴的正方向：

• X 轴指向机器人前进方向
• Z 轴向上
• Y 轴由右手定则确定

首先我们先定义两个非常重要的坐标系：

• 以基体质心为原点定义机器人坐标系{B}，
• 将坐标系{B}投影至支撑面，我们得到世界参考坐标系{W}；

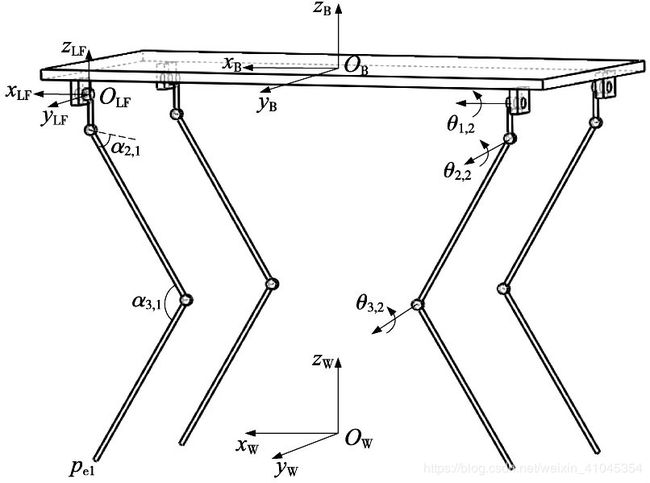
接下来定义4条腿顺序编号（左前LF、右前RF、右后RH、左后LH）依次为１～４，坐标系分别为{LF}、{RF}、{RH}、{LH}。各个坐标系位置如下图所示。

图片来自参考文献[1]

确定支撑多边形

①根据关节角度值由正运动学求出末端点$p_{ei}$，其中i = 1,2,3,4。在单腿坐标系{i}下的坐标表示${}^i{P}_{ei}$。

②根据坐标系间的几何关系，先求出{B}中的各个足端坐标${}^B{P}_{ei}$，

③然后在根据坐标系间的变换求出相对于{W}的足端位置${}^W{P}_{ei}$，

④最后由各支撑点坐标确定出支撑多边形．

二、零力矩点

在世界参考系{W}下，假设四足机器人的总重量为Ｍ，

• 所受重为$g=[0,0,-g{]}^T$，
• 中心坐标为$p_c=[x_c,y_c,z_c{]}^T$，
• zmp所在位置$p=[x_p,y_p,z_p{]}^T$，
• 支撑点受到地面反作用力合力为$f$，

则地面反作用力绕远点的力$\tau$为：

$$\tau =p\times f+{\tau }_p$$

其中${\tau }_p$为过零力矩点的力矩。

动量定理：如果一个系统不受外力或所受外力的矢量和为零，那么这个系统的总动量保持不变，公式为：$F_t=mv\prime －mv=p\prime －p$

角动量定理：质点系对一点（或一轴）的角动量对时间的导数等于外力系对此点（或此轴）的主矩

根据动量定理和角动量定理，有以下关系：

$$\dot{P}=Mg+f$$

$$\dot{L}=p_c\times Mg+\tau$$

综合上式，消去$\tau$和$f$得：

$${\tau }_p=\dot{L}-p_c\times Mg+(\dot{P}-Mg)\times p$$

由ZMP理论，令上式中的水平分量${\tau }_{px}$和${\tau }_{py}$为 ０，解得ZMP位置坐标$x_p$和$y_p$，

$$\{\begin{array}{c}{x}_p=\frac{Mg{x}_c+z_p\dot{P_x}-\dot{L_y}}{Mg+\dot{P_z}}\\ \\ y_p=\frac{Mg{y}_c+z_p\dot{P_y}+\dot{L_x}}{Mg+\dot{P_z}}\end{array}\text{\hspace{1em}(1)}$$

其中$z_p$为支撑面离地高度，当机器人出于平面时，$z_p=0$。把四足机器人简化成一个质点，其动量和角动量分别为：

$$\{\begin{array}{c}P=M\dot{p_c}=M[\dot{x_c}\dot{y_c}\dot{z_c}{]}^T\\ \\ L=p_c\times M\dot{p_c}=M[\dot{x_c}\dot{y_c}\dot{z_c}{]}^T\end{array}\text{\hspace{1em}(2)}$$

将（2）代入（1）中：

$$\{\begin{array}{c}{x}_p=x_c-\frac{(z_c-z_p)\ddot{x_c}}{\ddot{z_c}+g}\\ \\ y_p=y_c-\frac{(z_c-z_p)\ddot{y_c}}{\ddot{z_c}+g}\end{array}$$

根据上式可知，若已知重心坐标$p_c$和地面高度$z_p$以及重力加速度$g$，即可求出ZMP的坐标．

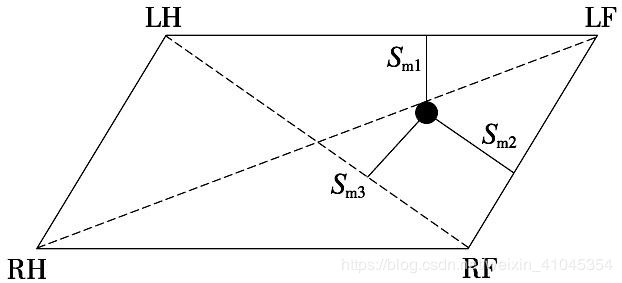
结合上一节所求的支撑多边形，我们可以判断四足机器人是否失稳．为了定量得衡量机器人保持稳定能力的大小，我们采用稳定裕度（stability margin）$S_m$作 为 标 准．如下图所 示，对4足机器人来说，定义稳定裕度为 ＺＭＰ距离支撑三角形边界的最短距离，即

$$S_m=min（S_{m1},S_{m2},S_{m3}）$$

参考文献

[1]王立鹏,王军政,赵江波,等.基于零力矩点的四足机器人非平坦地形下步态规划与控制[J].北京理工大学学报,2015,35(6):602-606.

---

如果觉得ok，点个赞，点个关注，也欢迎给个打赏支持一下编者的工作