Real-Time Loop Closure in 2D LIDAR SLAM 翻译和总结（二）

5.2 分支定界扫描匹配

像素级（pixel-accurate）匹配优化公式为：
$${\xi }^{\ast }=argmax(\xi \in \omega )\sum _{k=1}^K{M}_{nearest}(T_{\xi }{h}_k)\text{\hspace{1em}(BBS)}$$
上式中$\omega$表示搜索窗口，$M_{nearest}$是将转换后的坐标M拓展到$R^2$空间。通过将计算得到的坐标舍入到距离最近的栅格中，然后将该栅格点拓展到其对应的Pixel（附近距离最近的其他栅格点？）。匹配的质量可以进一步通过公式$CS$来优化提高。适当的选取遍历步长，可以有效提高效率。文中选择当激光雷达以最大的探测距离$d_{max}$扫描时移动不超过一个像素的宽度($r$, 也是一个最小分辨率栅格的宽度？) 为限制时对应的方向转角为角度遍历步长${\delta }_{\theta }$。基于余弦定理，可以得到：$$d_{max}=max(k=1,...,K)||h_k||\text{\hspace{1em}(6)}$$$${\delta }_{\theta }=arccos(1-\frac{r^2}{a{d}_{max}^2})\text{\hspace{1em}(7)}$$接着，可以基于给定的位移和角度搜索窗口大小计算积分次数，比如$W_x=W_y=7m，W_{\theta }=30°$:$$w_x=\frac{W_x}{r},w_y=\frac{W_y}{r},w_{\theta }=\frac{W_{\theta }}{r}\text{\hspace{1em}(8)}$$这会产生一个有限集合$\omega$，基于在当前最新估计位置${\xi }_0$为中心的搜索窗口：$$\bar{\omega }=\{-w_x,...,w_x\}\times \{-w_y,...,w_y\}\times \{-w_{\theta },...,w_{\theta }\}\text{\hspace{1em}(9)}$$$$\omega =\{{\xi }_0+(r{j}_x,r{j}_y,{\delta }_{\theta }{j}_{\theta }):(j_x,j_y,j_{\theta })\in \bar{\omega }\}\text{\hspace{1em}(10)}$$基于传统方法进行暴力遍历寻找最优的匹配${\xi }^{\ast }$实现较为简单，可见下述算法1，但是窗口越大，搜索效率越慢：
算法1:暴力匹配方法

与上述方法不同的是，作者采用一种分支定界的方法来实现在更大的搜索窗口有效计算${\xi }^{\ast }$。算法2描述了此方法的一般实现过程。该方法首次在混合整型线性规划问题中使用[17]。关于这方面的文献较多，可以参见[18]中的文献概述。
算法2：一般分支定界算法
该方法的主要思想是，在一个树结构里，根节点表示所有可能的概率（$\omega$），孩子节点表示概率子集。每个节点的孩子节点组成双亲节点的一个分支，因此这些孩子节点一起可以表示相同的概率集合。叶节点是单独的，每一个表示单独的结果。算法是严格的，只要内部节点c的得分$score(c)$是它元素（其孩子）得分的上界，则和暴力匹配方法一样可以提供相同的结果。在这种情况下，无论什么时候一个节点成为边界，则比已知的最优的结果更优的结果不会出现在其他子树中。

具体而言，论文中的算法过程可分为以下步骤：1）节点选择（node selection）; 2) 分支（branching）; 3) 计算上界（computation of upper bounds）。

1）节点选择（Node Selection）：作者采用深度优先搜索（DFS）作为无先验信息下的默认搜索方式：此时搜索效率高低很大一部分取决于树的结构。这由两件事情决定：一个是好的上界； 一个是好的当前结果。后者可以有助于深度优先搜索，这样能够很快的对许多叶子节点进行评估计算。因为在回环里加入低匹配度的约束可能反而导致错误，所以作者也设了最低分数阈值，低于此阈值的匹配结果不会在优化过程中使用。实际中的得分并不会频繁超过此阈值，这能够降低节点选择或者寻找初始启发解的重要程度（这样可以提高节点的筛选效率）。基于深度优先搜索遍历孩子节点的顺序，计算每个孩子节点得分的上界，并首先遍历拥有最大边界的最有可能匹配的孩子节点。该方法具体见算法3所示。
算法3：深度优先的分支定界算法

2）分支规则（Branching rule）：树中的每个节点都用一个整型元组表示$c=(c_x,c_y,c_{\theta },c_h)\in Z^4$。高度为$c_h$的节点除了表示一个旋转之外，还一起表示$2^{c_h}\times 2^{c_h}$个可能的位移变换：

$${\overline{\stackrel{ˉ}{\omega }}}_c=(\{(j_x,j_y)\in Z^2:c_x\le j_x<c_x+2^{c_h},c_y\le j_y<c_y+2^{c_h}\}\times c_{\theta })\text{\hspace{1em}(11)}$$

$${\bar{\omega }}_C={\overline{\stackrel{ˉ}{\omega }}}_c\bigcap \bar{\omega }\text{\hspace{1em}(12)}$$

叶节点高度为0，即$c_h=0$, 对应最终的匹配结果${\xi }_c={\xi }_0+(r{c}_x,r{c}_y,{\delta }_{\theta }{c}_{\theta })\in \omega$。

在图示的算法3中，包含所有可能结果的根结点，不会显式的出现，而是会以一个固定的高度$h_0$（此相当于初始的粗分辨率，将搜索窗口均匀的粗划分形成初始节点集合$C_0$；具体大概设为多少论文没说）分为一组覆盖搜索窗口的初始节点$C_0$集合：

$${\bar{\omega }}_{0,x}=\{-w_x+2^{h_0}{j}_x:j_x\in Z,0\le 2^{h_0}{j}_x\le 2w_x\},$$

$${\bar{\omega }}_{0,y}=\{-w_y+2^{h_0}{j}_y:j_y\in Z,0\le 2^{h_0}{j}_y\le 2w_y\},$$

$${\bar{\omega }}_{0,\theta }=\{j_{\theta }\in Z,-w_{\theta }\le j_{\theta }\le w_{\theta }\},$$

$$C_0={\bar{\omega }}_{0,x}\times {\bar{\omega }}_{0,y}\times {\bar{\omega }}_{0,\theta }\times h_0.\text{\hspace{1em}(13)}$$

基于给定的节点$c(c_h>1)$, 将其分为不超过4个高度为$c_h-1$的孩子节点：
$$C_c=((\{c_x,c_x+2^{c_h-1}\}\times \{c_y,c_y+2^{c_h=1}\}\times c_{\theta })\bigcap \bar{\omega })\times \{c_h-1\}\text{\hspace{1em}(14)}$$
上式可以理解为，每当C集合中出现$score(c)>best\_score$时，则对当前节点c进行分支，分支的规则是：$c_{\theta }$保持与c节点一致，对$c_h-1$，此相当于提高遍历分辨率，也就是下沉到更深的节点（DFS思想），从而形成新的更高分辨率的子窗口集合，这里不超过4个就是因为以2分的思想（$2^{c_h-1}$）来处理，所以x, y方向各最多增加2个孩子节点，则一共最多分为4个孩子节点。然后新的C集合变为$C_c$与上一个C集合的并集继续按照得分高低遍历循环。
3）计算上界（Computing upper bounds）：分支定界剩下的部分是在内部节点如何有效计算上界，包括考虑到计算复杂度和上界质量。上界的具体计算公式为：

$$score(c)=\sum _{k=1}^{K}ma{x}_{j\in {\overline{\stackrel{ˉ}{\omega }}}_c}{M}_{nearest(T_{{\xi }_j}{h}_k)}\ge \sum _{k=1}^{K}ma{x}_{j\in {\bar{\omega }}_c}{M}_{nearest(T_{{\xi }_j}{h}_k)}\ge ma{x}_{j\in {\bar{\omega }}_c}\sum _{k=1}^K{M}_{nearest(T_{{\xi }_j}{h}_k)}\text{\hspace{1em}(15)}$$

为了高效率计算最大值，作者使用了栅格预计算(precomputed grids $M_{precomp}^{c_h}$)方法。在每个可能的高度$c_h$对每个栅格预计算，可以使得计算得分的复杂度与扫描点数量成线性增长关系(这样计算得分的时间复杂度和之前的待匹配栅格图无关，因为已经预计算了)。需要注意的是，为了这样处理，作者也在整个${\overline{\stackrel{ˉ}{\omega }}}_c$（当前节点对应的搜索窗口）计算最大值，这在搜索空间的边界附近可能会大于${\bar{\omega }}_c$框出来的范围。

$$score(c)=\sum _{k=1}^K{M}_{precomp}^{c_h}(T_{{\xi }_c}{h}_k),\text{\hspace{1em}(16)}$$

$$M_{precomp}^h（x,y）=ma{x}_{\{x^{\prime }\in [x,x+r(2^h-1)],y^{\prime }\in [y,y+r(2^h-1)]\}}{M}_{nearest}(x^{\prime },y^{\prime })\text{\hspace{1em}(17)}$$

上式中${\xi }_c$与之前的叶子节点相同。$M_{precomp}^h$和$M_{nearest}$有相同的像素结构，但是在每一个像素里都存储$2^h\times 2^h$的box里的最大值。此处$h_k$对应的是当前的scan, 每次扫描更新都会随时间更新，$M_{precomp}^h(T_{{\xi }_c}{h}_k)$会在更新之前预计算当前机器人位置对应回环搜索空间的树结构中每个节点对应的搜索窗口里x,y位置对应的栅格概率图，等scan更新之后基于每个待搜索转换关系$T_{{\xi }_c}$得到每个节点对应位置$T_{{\xi }_c}{h}_k$=（x, y），接着在$M_{precomp}^{c_h}$直接查找对应的概率值进行累加即可，不用重新计算。这样的预计算的栅格结果如图3所示：

图3 当前节点搜索窗口下栅格大小分别为1，4，16，64的预计算概率结果（对应$c_h$分别为0，2，4，6）

为了使得构造预计算栅格的计算复杂度较低, 会等每个概率栅格不再收到更新（也就是scan不再扫描到这个栅格）才会进行预计算。接着计算预计算栅格集合，而且基于此开始匹配。

对每一个预计算栅格，计算以每个pixel为起始的$2^h$像素宽度的下的最大值（类似于图像中的$2^h\times 2^h$的卷积核滑动滤波？）。使用这个中间结果，则下一个预计算栅格也就被顺便构造出来了。

如果动态变化的一组值删除的顺序与添加的顺序一致，则它们的最大值可以保持每次以$O(1)$的复杂度更新。连续的最大值保存在一个队列里，该队列可以递归的被定义为包含集合里当前所有值的最大值。当第一个最大值产生时，队列后面便会跟着所有持续更新的所有当前值的连续最大值列表。如果当前值的集合是空的，则对应的列表也是空的。基于此方法，则预计算栅格的复杂度可以控制在$O（n）$, n为每个预计算栅格的像素pixel数量。

另外一个可选的上界计算方法是，可以在更低分辨率的概率栅格上计算得分上界，并继续将分辨率降低一半得到下一个上界, 可参见[1]。作者认为本文使用的上界计算方法（公式（15））增加的额外内存消耗是可接受的，所以更倾向于使用公式（15），因为基于低分辨率概率栅格的方法相对公式（15）会产生更差的边界值，因此对系统性能产生负面影响。

6. 实验结果

作者使用三种数据进行了实验验证，一是在慕尼黑德国博物馆使用Cartographer 的背包进行扫描的数据；二是使用一般性能的扫地机器人传感器获得的数据；三是使用Radish数据集进行了测试，并与已经公布的其他方法进行了对比。

1）真实场景测试：慕尼黑德国博物馆

图4展示了慕尼黑博物馆2253m，1913秒的数据结果。运行机器是主频3.2GHz的Intel Xeon E5-1650工作站，SLAM算法使用了1018s的CPU时间，2.2G内存，4个线程进行回环匹配。总共花了1个小时跑完了数据，表示具有5.3倍的实时性能。

用于回环优化的图大概包含11456个节点，和35300个边。当每隔几个节点加入到图中时，SPA(Sparse Pose Adjustment)优化便会允许一次。优化过程典型值为：迭代3次，耗费0.3s。
图4 慕尼黑博物馆2D的Cartographer Map

2）真实场景测试：Neato’s Revo LDS

Neato’s Revo LDS是一个激光雷达传感器，一般用于清扫，其价格大概在30美元。作者以2Hz的采样率采集数据运行算法，生成了图5所示的5cm分辨率的2D平面图。使用激光笔测距和算法输出的结果，比较了5条直线的长度，结果如表1所示，大致精度在每条线上是1个像素的误差。
图5 基于Revo LDS的Cartographer map

表1 Revo LDS 误差

3）Radish数据集测试

作者将本文方法和其他方法进行了对比, 参考[21]， 比较了基于真值轨迹的相对位姿误差。表2/3展示了位姿对比结果。

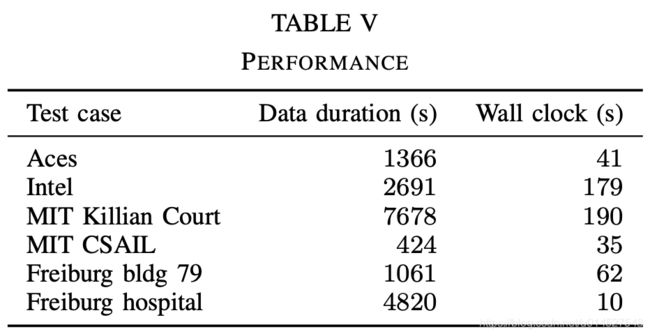
因为文中采用submaps和scans间添加回环约束的方法，所以没有具体的数据集指标量化，也很难与其他scan-to-scan的方法进行比较。表4列出了每次测试的回环数量（包括正确约束和错误约束），以及精度（其中正确约束的占比）。关于是否是正确回环约束，作者认为在计算SPA优化时，这些约束不超过20cm或者1度。尽管文中的scan-submap匹配步骤会添加一些错误的约束，但是整体上保证了SPA在所有的测试里能够具有大量的回环约束（回环数量和质量不能兼得）。此外，同时在SPA中使用了$Huberloss$处理回环中的异常点。在Freiburg hospital的例子中，回环中的低分辨率和低最小得分设置产生了过高的假阳性率。这可以通过增大回环中的min score设置来提升精度，但是这会降低某些维度的结果质量（回环数量减少，某些局部误差容易变大）。同样，没有针对CPU性能调试Cartographer SLAM的参数，表5提供了算法消耗的时钟时间（机器依旧是测试1中的工作站）。
表2 位姿精度

表3 位姿精度

表4 回环精度

表5 算法时间性能

7. 结论

作者提出了一个2D SLAM系统，包含scan-to-submap的匹配，回环检测，和图优化。独立的submao轨迹使用基于栅格的local SLAM方法。在后端，所有的扫描帧scan都会使用像素级匹配方法与附近的submaps匹配去建立回环约束。submap和scan位姿的约束图会在后端间断性持续优化。当同时用GPU进行加速合并已经完成的submaps和当前submap时，操作人员可以即时预览最终的地图效果。并且通过实验验证了本文算法可以在一般性能的硬件平台实时运行。