JZOJ5965【NOIP2018提高组D2T2】填数游戏

题目

作为NOIP2018的题目，我觉得不需要把题目贴出来了。
大意就是，在一个$n\ast m$的$01$矩阵中，从左上角到右下角的路径中，对于任意的两条，上面的那条小于下面的那条。问满足这样的矩阵的个数。
好吧，有点简陋……

---

比赛思路

一眼看下去，诶，$n$这么小，一下子就想到了状压DP。
然后有一点很显然：$(i,j)\le (i+1,j-1)$。
依照这个性质，我打出了一个状压DP。
然后发现，第二个样例崩了。
然后手算了半天，推出来另一个朦胧的性质……
然后看看时间，啊，不能再推式子了！没时间啦！
匆匆打个暴力，去思考第三题。

---

正解

这题的正解有很多种。
的确有状压DP，不过最优的方法还是lyl推了两节数学课的神方法。
用这个方法，就算开到long long范围，也可以秒过。

其实这题还有一个性质：
如果$(i,j)=(i+1,j-1)$，那么以$(i+1,j)$为左上角的矩形的所有对角线上的数字相等。
至于为什么，也是比较好理解的。
如果有条到$(i,j-1)$的路径，可以分成两条分别走到$(i,j)$和$(i+1,j-1)$，再走到$(i+1,j)$，在这个时候它们是相等的。如果这个矩形中有不相等的路径，那么必定存在一种方案使通过$(i,j)$的走小的，通过$(i+1,j-1)$的走大的，不符合条件。所以在这个矩形中的左上角到右下角的路径相等，要让路径相等，对角线就要相等。

有了这个条件，这道题就变得复杂起来。lyl大佬发挥出他超强的推式子能力，把这题A穿了。
首先，我们可以分类讨论。
先讨论$n=m$的情况

1. 当$(0,1)=(1,0)$时
   在这个情况比较简单，答案为$2\ast 2\ast 4^{n-2}\ast 2^{n-1}$
2. 当$(0,1)̸=(1,0)$时

   1. 当$(0,2)=(1,1)=(2,0)$时
      也比较简单，$2\ast 2\ast 5\ast 4^{n-4}\ast 2^{n-1}$

   2. 当$(1,1)=(2,0)$时
      
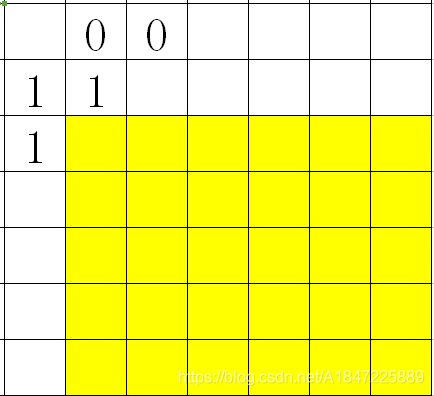
      黄色表示这片区域内的对角线相等。
      设$f_i$表示到$i$这条对角线，$i-1$或之前对角线的上面两个一样的方案数。
      （这里的对角线为$(0,3)$到$(0,n-1)$为右上角的两个对角线，编号从$1$开始）
      那么$f_i=f_{i-1}\ast 4+4\ast 5$
      $f_{i-1}\ast 4$表示$i-2$或之前已经有了对角线上面两个一样的，那么第$i$条对角线被限制了，所以只有$4$种。
      $4\ast 5$表示$i-1$有上面两个一样，那么第$i$条不受限制，有$5$种。

      接下来我们计算这种情况的方案数：
      $2\ast (3+4\ast 3+f_{n-3}\ast 2)\ast 2^{n-2}$
      估计问题在$(3+4\ast 3+f_{n-3}\ast 2)$这里面。
      $3$表示以$(0,n-1)$为右上角的对角线的上面两个不一样，之前的也不一样，那么以$(1,n-1)$为右上角的对角线不受影响，方案为$3$
      $4\ast 3$表示以$(0,n-1)$为右上角的对角线的上面两个一样，之前的不一样，那么以$(1,n-1)$为右上角的对角线还是不受影响，方案为$4\ast 3$
      $f_{n-3}\ast 2$表示以$(0,n-2)$或之前有对角线上面两个一样的，那么以$(1,n-1)$为右上角的对角线受到限制，方案为$f_{n-3}\ast 2$

   3. 当$(0,2)=(1,1)$时
      可以发现和上面的情况对称，所以也是$2\ast (3+4\ast 3+f_{n-3}\ast 2)\ast 2^{n-2}$

---

这样$n=m$的情况就考虑完了。
接下来考虑$n+1=m$的情况。

1. 当$(0,1)=(1,0)$时
   
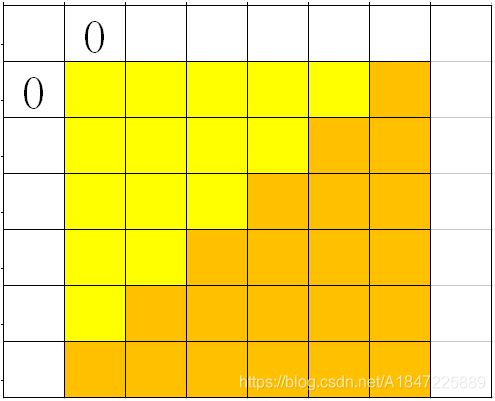
   我们可以将深黄色的这一部分向右平移
   
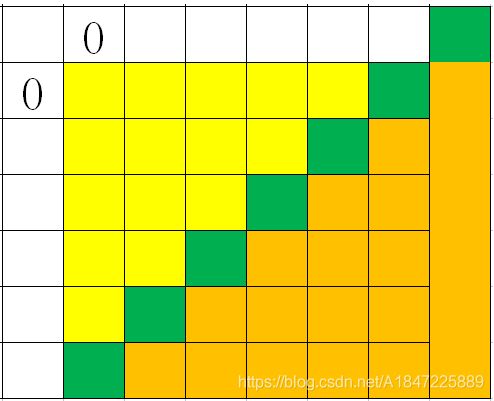
   然后你就可以发现多出来的实际上是中间绿色的这一部分。
   显然这一部分的方案数为$3$，所以答案$\ast 3$
2. 当$(0,1)̸=(1,0)$时
   1. 当$(0,2)=(1,1)=(2,0)$时，和上面的差不多，也是$\ast 3$。
   2. 当$(1,1)=(2,0)$时
      答案为$2\ast (3+3\ast 3+(4\ast 4+f_{n-3}\ast 3)\ast 2)\ast 2^{n-2}$
      分类讨论：
      1. $(0,n)$为右上角的对角线的上面两个不一样，之前的也不一样。
      2. $(0,n)$为右上角的对角线的上面两个一样，之前的不一样。
      3. $(0,n-1)$或之前为右上角的对角线的上面有两个一样的。
   3. 当$(0,2)=(1,1)$时
   4. 答案为$2\ast (4+4\ast 4+f_{n-3}\ast 3)\ast 2^{n-1})$
      类似类似（比上一种简单）

---

在推完这些东西之后，我们就可以发现，在$m=n+1$之后，$m$每$+1$，答案$\ast 3$
证明？
分各种情况讨论，是可以证出来的……
要了我好久的时间……
懒得打上来了，留给自已以后温故的时候思考。

反正，最终的时间复杂度是$O(\lg n+\lg m)$（求$f$的时候其实可以用矩阵来求）的，非常优秀。
所以lyl说这题的数据太小了，我看可以大一些，大到什么程度呢？
给你读入两个位数十万的二进制数，分别表示$n$、$m$。

---

代码

using namespace std;
#include 
#include 
#include 
#define mo 1000000007
inline long long my_pow(long long x,int y){
	long long res=1;
	for (;y;x=x*x%mo,y>>=1)
		if (y&1)
			res=res*x%mo;
	return res;
}
#define N 8
int n,m;
long long f[N+1];
int main(){
	freopen("game.in","r",stdin);
	freopen("game.out","w",stdout);
	scanf("%d%d",&n,&m);
	if (n>m)
		swap(n,m);
	if (n==1)
		printf("%lld\n",my_pow(2,m));
	else if (n==2)
		printf("%lld\n",12*my_pow(3,m-2)%mo);
	else if (n==3)
		printf("%lld\n",112*my_pow(3,m-3)%mo);
	else{
		long long a1=2*2*my_pow(4,n-2)*my_pow(2,n-1)%mo;/*(0,1)(1,0)相同时*/
		long long a2=2*2*5*my_pow(4,n-4)%mo*my_pow(2,n-1)%mo;/*(0,2)(1,1)(2,0)相同时*/
		for (int i=2;i<=n-3;++i)
			f[i]=f[i-1]*4/*之前有过，所以这一位受到了限制*/+4*5/*i-1相同*/;
		if (n==m){
			long long ans=2*2*(3/*上面的n-3个对角线全部不一样*/+4*3/*第n-3个对角线一样*/+f[n-3]*2/*n-3之前的有过一样*/)%mo*my_pow(2,n-2)%mo;//(0,2)(1,1)(2,0)其中有两个相同时 
			printf("%lld\n",(a1+a2+ans)%mo); 
		}
		else{
			long long ANS1=2*(3/*(1,n)之前没有一样*/+3*3/*(0,n)和(1,n-1)一样*/+(4*4/*(0,n-1)和(1,n-2)一样*/+f[n-3]*3)*2)%mo*my_pow(2,n-2)%mo;
			long long ANS2=2*(4+4*4+f[n-3]*3)%mo*my_pow(2,n-1);
			printf("%lld\n",((a1+a2)*3+ANS1+ANS2)*my_pow(3,m-n-1)%mo);
		}
	}
	return 0;
}

---

在此再%一下lyl大爷，两节数学课顶的过我们的几天。