HDU 6286 2018(容斥)

2018
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 229 Accepted Submission(s): 120

Problem Description
Given a,b,c,d, find out the number of pairs of integers (x,y) where a≤x≤b,c≤y≤d and x⋅y is a multiple of 2018.

Input
The input consists of several test cases and is terminated by end-of-file.

Each test case contains four integers a,b,c,d.

Output
For each test case, print an integer which denotes the result.

Constraint

• 1≤a≤b≤109,1≤c≤d≤109
• The number of tests cases does not exceed 104.

Sample Input
1 2 1 2018
1 2018 1 2018
1 1000000000 1 1000000000

Sample Output
3
6051
1485883320325200

题意

给你a,b,c,d 问你从 [a,b] [ a , b ] 和 [c,d] [ c , d ] 两个范围中取出两个数x和y相乘为2018倍数的个数

思路

首先分解一下2018这个数，2018一共有1，2，1009，2018四个因子，所以我们首先要找出 [a,b] [ a , b ] 中1，2，1009，2018，的因子数，因子这里就需要去重，因为你找含有1这个因子的数时，会把含有2的因子的含有1009的和2018的数都算上，所以含有1的因子数要去掉含有2，1009，2018的因子的个数，同样的找2这个因子数时也会就会把2018也算上，所以要去掉2018这个数，1009也是要去掉2018的
也就是

        x[0]=b-a+1;
        x[1]=b/2-(a-1)/2;
        x[2]=b/1009-(a-1)/1009;
        x[3]=b/2018-(a-1)/2018;
        x[2]-=x[3];
        x[1]-=x[3];
        x[0]-=x[3]+x[2]+x[1];

注意顺序先把2和1009处理了再处理1的
两个区间都进行这样的操作后我们就有4*4里面的组合来凑出答案了

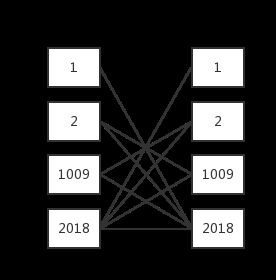
一共有9种组合我们把相应的数乘起来相加即可

#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
int main()
{
    long long a,b,c,d;
    while(scanf("%lld%lld%lld%lld",&a,&b,&c,&d)!=EOF)
    {
        long long x[4];
        long long y[4];
        x[0]=b-a+1;
        x[1]=b/2-(a-1)/2;
        x[2]=b/1009-(a-1)/1009;
        x[3]=b/2018-(a-1)/2018;
        x[2]-=x[3];
        x[1]-=x[3];
        x[0]-=x[3]+x[2]+x[1];
        y[0]=d-c+1;
        y[1]=d/2-(c-1)/2;
        y[2]=d/1009-(c-1)/1009;
        y[3]=d/2018-(c-1)/2018;
        y[2]-=y[3];
        y[1]-=y[3];
        y[0]-=y[1]+y[2]+y[3];
        long long ans=0;
        ans+=x[1]*y[2];
        ans+=x[1]*y[3];
        ans+=x[2]*y[1];
        ans+=x[2]*y[3];
        ans+=x[3]*y[1];
        ans+=x[3]*y[2];
        ans+=x[3]*y[3];
        ans+=x[3]*y[0];
        ans+=x[0]*y[3];
        printf("%lld\n",ans);
    }
    return 0;
}