【论文笔记之RNNoise】A Hybrid DSP/Deep Learning Approach to Real-Time Full-Band Speech Enhancement

本文对Jean-Marc Valin于2018年发表的基于深度学习降噪的论文进行简单地翻译。如有不当之处欢迎批评指正

1. 论文目的

  将深度学习与传统的信号算法融合以达到更好的降噪性能，用深度学习来替代降噪过程中传统信号算法需要精调的部分。

2. 摘要

  尽管噪声抑制已经是信号处理中一个成熟的领域，但仍然需要对它的估计算法和参数进行调优。文章演示了一种融合DSP /深度学习来抑制噪声的方法。该方法在致力于保持尽可能低的计算复杂度的同时，实现了高质量的增强语音。使用具有四个隐藏层的深层递归神经网络来估计理想临界频带增益，而用传统的基频滤波器抑制谐波之间的噪声。 与传统的最小均方误差谱估计器相比，该方法可显着提高语音质量，同时将复杂度保持在足够低的水平。

3. 介绍

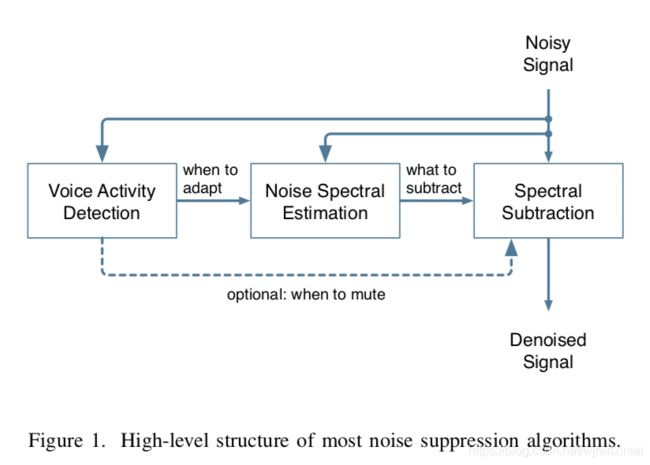
  至少从 70年代开始，噪声抑制就成为人们关注的话题。尽管质量有了显著提升，但算法结构基本保持不变。一些谱估计技术依赖于噪声谱估计器，而噪声谱估计器由语音活动检测器（ VAD）或类似的算法驱动，如图 1所示。 3个模块中的每个模块都需要准确的估计器，并且很难去调。尽管研究者们改进了这些估计器，但仍然很难设计它们，并且该过程需要大量的人工调优。这就是为什么最近深度学习技术上的进展对噪声抑制具有吸引力的原因。

  深度学习技术已被用于噪声抑制。许多方法都针对不需要低延迟的自动语音识别（ASR）应用。而且，在许多情况下，如果没有GPU，神经网络的庞大规模将使得实时实现变得困难。文章专注于低复杂度的实时应用（例如视频会议），还专注于全频带（48 kHz）语音。为了实现这些目标，文章选择了一种混合的方法，该方法依靠信号处理技术并使用深度学习来替代传统上难以调优的估计器。该方法与所谓的端到端系统形成对比，在端到端系统中，大多数或所有信号处理操作都被机器学习取代。这些端到端系统已经明确地展示了深度学习的能力，但是它们通常以显著地增加复杂度为代价。

  文章所提出的方法具有可接受的复杂度，并且比传统方法效果更好。

4. 信号模型

  文章提出的方法将深度学习技术用于传统噪声抑制中需要人为调优的部分，而其余部分则使用信号处理技术。

  算法使用20ms的帧长，10ms的帧移。分析窗和合成窗都使用Vorbis窗，它满足Princen- Bradley准则。该窗定义如下：
$$w(n)=sin[\frac{\pi }{2}si{n}^2(\frac{\pi n}{N})]\text{\hspace{1em}(1)}$$
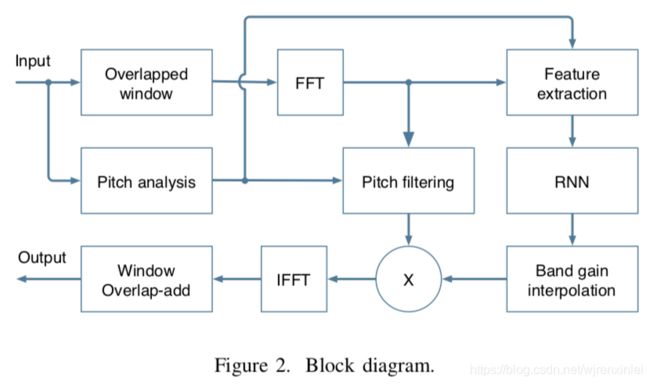
其中$N$是窗长。文章所提出的系统如图2所示。大部分的抑制是通过使用RNN计算出来的增益作用在低分辨率的谱包络上来完成的，这些增益是理想比例掩码 （IRM）的平方根。在此基础上使用梳状滤波器来抑制谐波之间的噪声以达到更加精细的抑制。

A. Band structure

  为了避免过高的计算复杂度，假设语音和噪声的频谱足够平坦，以使用较粗的频率分辨率。与其它一些方法直接估计谱幅度不同，文章直接估计理想临界带的增益，其取值范围在0到1之间。将频谱以类似于Bark scale的尺度进行划分，也就是说在高频部分，带的划分和Bark scale一样，但在低频部分，至少有4个频点。文章使用三角形带，并且峰值响应位于相邻带的边界。这样总共会产生22个带，因此，只需输出22个位于0和1之间的值即可。

  令$w_b(k)$为带$b$频点$k$处的幅度，有${\sum }_b{w}_b(k)=1$，对于信号$X(k)$，带的能量是：
$$E(b)=\sum _k{w}_b(k){\left|X(k)\right|}^2\text{\hspace{1em}(2)}$$
每个带的增益定义为：
$$g_b=\sqrt{\frac{E_s(b)}{E_x(b)}}\text{\hspace{1em}(3)}$$
其中$E_s(b)$是干净语音能量，$E_x(b)$是含噪语音能量。考虑一个理想的带增益${\hat{g}}_b$，将下面的内插增益应用到每个频点$k$上:
$$r(k)=\sum _b{w}_b(k){\hat{g}}_b\text{\hspace{1em}(4)}$$

B. Pitch filtering

  使用基于Bark域推导出来的带来计算增益的一个比较明显的缺点就是它不能很好地建模谱的细节。在实际中，这会导致谐波之间的噪声不能被很好地抑制。文章使用梳妆滤波器来抑制谐波之间的噪声，此举类似于语音编解码器中后置处理器的操作。由于语音信号的周期严重依赖于频率，基于每个带的滤波器系数${\alpha }_b$在频域进行pitch filtering操作。令$P(k)$是$x(n-T)$（the pitch-delayed signal）的加窗DFT的结果。滤波操作首先计算$X(k)+{\alpha }_{b}P(k)$，然后归一化计算出来的结果以使其在每个带上的能量与原始信号$X(k)$的能量一样。

  带$b$的pitch correlation定义为：
$$p_b=\frac{{\sum }_k{w}_b(k)\Re [X(k)P^{\ast }(k)]}{\sqrt{{\sum }_k{w}_b(k){\left|X(k)\right|}^2\cdot {\sum }_k{w}_b(k){\left|P(k)\right|}^2}}\text{\hspace{1em}(5)}$$
其中
$\Re [\cdot ]$表示复数的实数部分；
$\ast$表示复数共轭。
注意到对于单个带，$（5）$式将等于时域的pitch correlation。

  推导${\alpha }_b$的值是比较难的，并且最小化均方误差的值在感知上也不是最优的。相反，作者使用基于以下约束和观察的启发式方法。因为噪声会造成pitch correlation降低，作者不期望在平均意义上$p_b$大于$g_b$，因此，对于任意带只要$p_b\ge g_b$,就令${\alpha }_b=1$。当没有噪声的时候，不希望对语音产生损伤，因此，当$g_b=1$时，令${\alpha }_b=0$。下式滤波器系数表达式遵从所有这些约束：
$${\alpha }_b=\min (\sqrt{\frac{p_b^2(1-g_b^2)}{(1-p_b^2)g_b^2}},1)\text{\hspace{1em}(6)}$$
除了使用FIR pitch filter外，也可以使用具有$H(z)=1/(1-\beta z^{-T})$形式的IIR pitch filter来计算$P(k)$，这可以更好地抑制谐波之间的噪声，但与此同时会稍微增加失真。

C. Feature extraction

  为了提高训练数据的条件，对log谱进行DCT变换，
  1）生成22个Bark域的倒谱系数(BFCC)；
  2）对前6个BFCCs求一阶和二阶时间导；
  3）由于需要计算式 （5）中的pitch，特征中还包括整个频带pitch correlation的DCT变换的前6个系数；
  4）特征中还包含基因周期以及频谱非平稳性度量，这有助于语音检测。总共有42个输入特征。

  考虑到必须追踪噪声的绝对水平，选取这些特征是有意为之的，但这确实会使特征对信号的绝对幅度和通道频率响应敏感。

4. 深度学习架构

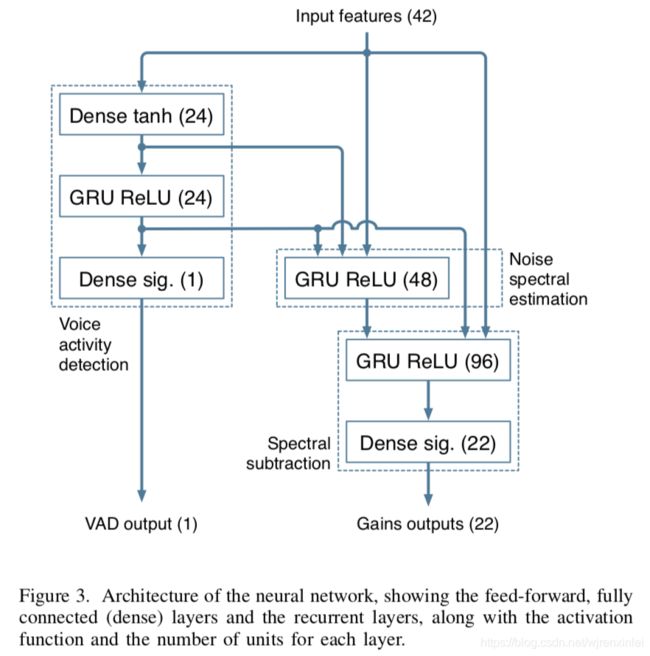
  如图3所示，文章提出的神经网络基本遵循传统降噪算法的架构。该设计基于以下假设：三个循环层分别对应图1中的每个模块。不过，在实际中神经网络可以自由地偏离该假设。它总共包括215个单元，4个隐藏层，最大的一层有96个单元。单元数量的增加并不能有效提高降噪性能。然而，损失函数以及构建训练数据的方式对最终的性能有很大的影响。在这个任务上，作者发现GRU比LSTM性能稍好点，并且更加简单。

  尽管不是必须的，但网络仍包括了一个VAD输出。所增加的额外复杂度很小，并且通过确保相应的GRU确实学会了从噪声中区分出语音，从而达到提高训练性能的目的。

A. 训练数据

  训练需要各种噪声和纯语音数据，将噪声和干净语音以不同的级别混合，以尽可能产生各种信噪比，包括纯语音和纯噪声片段。文章没有使用倒谱均值归一化，而是通过数据增强的方式使网络对频率响应的变化更加鲁棒，这是通过使用以下形式的二阶滤波器针对每个训练样本分别对噪声和语音信号滤波来实现的:
$$H(z)=\frac{1+r_1{z}^{-1}+r_2{z}^{-2}}{1+r_3{z}^{-1}+r_4{z}^{-2}}\text{\hspace{1em}(7)}$$
其中$r_1\cdots r_4$是在$[-\frac{3}{8},\frac{3}{8}]$范围内均匀分布的随机值。通过改变最终混合信号的级别使得网络对各种信号的幅度均鲁棒。

  有6个小时的原始干净语音和4个小时的原始噪声，通过使用各种增益和滤波器组合并将数据重采样到40 kHz至54 kHz之间，总共产生了140个小时的含噪语音。

B. 优化过程

  用于训练的损失函数决定了当前网络在无法准确确定合适的增益时，如何权衡过渡衰减与衰减不足。尽管在优化$[0,1]$范围内的值时通常使用二值交叉熵函数，但由于其与增益的感知效果不匹配，因此不会对增益产生好的结果。对于估计的增益${\hat{g}}_b$和真实值$g_b$，使用下列的损失函数进行训练：
$$L(g_b,{\hat{g}}_b)=(g_b^{\gamma }-{\hat{g}}_b^{\gamma }{)}^2\text{\hspace{1em}(8)}$$
其中，$\gamma$是一个控制噪声抑制程度的感知参数。因为${\lim }_{\gamma \to 0}\frac{x^{\gamma }-1}{\gamma }=\log (x)$，${\lim }_{\gamma \to 0}L(g_b,{\hat{g}}_b)$最小化对数能量的均方误差，这将使抑制过于激进，因为增益没有下限。实际上，$\gamma =1/2$提供了一个很好的权衡。有时候，在特定的带上可能没有噪声或者语音。当这种情况发生时，将这些带上的真实增益标记为未定义的，并且忽略该增益的损失函数以避免损害训练过程。

  对于网络的VAD输出，使用标准的交叉熵损失函数。

C. 增益平滑

  当使用${\hat{g}}_b$抑制噪声时，输出的信号有时候听起来干巴巴的(缺少必要的混响)，通过约束${\hat{g}}_b$帧间的衰减可以解决这个问题，平滑的增益如下:
$$g_b=\max (\lambda g_b^{(prev)},{\hat{g}}_b)\text{\hspace{1em}(9)}$$
其中，$g_b^{(prev)}$是前一帧的增益因子。衰减因子$\lambda =0.6$等于$135$ms的混响时间。

5. 后记

  该篇论文所对应的开源库rnnoise应该算是业内第一个基于深度学习的降噪算法开源库了。作者本人Jean-Marc Valin——音频算法领域实打实的牛人，不管是在算法层面还是工程层面都很强，speex以及opus都出自他之手。

  再说几个关于rnnoise可优化的点：
  1）是否有必要将VAD、噪声估计以及噪声抑制模块都用模型来替代，里面有的模块是否是冗余的，可参考其它相关文献；
  2）网络的输入特征包含了好几个部分，可否参考其它相关文献简化输入特征种类或者说抛弃信号式的提特征方式，改为网络提特征；
  3）模型结构能否改动，比如节点数增加 、层数增加以及单向gru变双向gru等。语音是一种时序关系较强的序列，单向gru只能看到历史信息看不到未来信息，但双向gru可以。但如果使用了双向gru，那么又该如何保证低延迟，实时性。
  4）如作者在文章最后提到的那样，能否扩展该网络，在输入特征中添加参考信号的特征或者其它特征，使其实现抑制残余回声的功能。
  。。。。。。