python计算机视觉编程(五)多图拼接
图像拼接整体流程
- 根据给定图像,实现特征匹配
- 通过匹配特征计算图像之间的变换结构
- 利用图像变换结构,实现图像映射
- 利用叠加后的图像,采用算法,对齐特征点
- APAP
- Lowe’s算法
- 通过图割方法,自动选取拼接缝
- 根据Multi-Band Blending策略实现融合
- 实验结果
- 实现代码
根据给定图像,实现特征匹配
详情参见python计算机视觉编程(三)Harris角点 SIFT 匹配地理标记图像: https://blog.csdn.net/qq_41409331/article/details/88618847.
通过匹配特征计算图像之间的变换结构
详情参见python计算机视觉编程(四)图像到图像的映射前半部分: https://blog.csdn.net/qq_41409331/article/details/88662767.
利用图像变换结构,实现图像映射
详情参见python计算机视觉编程(四)图像到图像的映射后半部分: https://blog.csdn.net/qq_41409331/article/details/88662767.
利用叠加后的图像,采用算法,对齐特征点
这里介绍两种常用的方法
APAP
- 提取两张图片的sift特征点
- 对两张图片的特征点进行匹配
- 使用RANSAC算法进行特征点对的筛选。筛选后的特征点基本能够对应。
RANSAC的基本假设是:
(1)数据由“局内点”组成,例如:数据的分布可以用一些模型参数来解释;
(2)“局外点”是不能适应该模型的数据;
(3)除此之外的数据属于噪声。
局外点产生的原因有:噪声的极值;错误的测量方法;对数据的错误假设。
RANSAC也做了以下假设:给定一组(通常很小的)局内点,存在一个可以估计模型参数的过程;而该模型能够解释或者适用于局内点。
可以参考 https://www.cnblogs.com/weizc/p/5257496.html. - 使用DLT算法,将剩下的特征点对进行透视变换矩阵的估计。
- 因为得到的透视变换矩阵是基于全局特征点对进行的,即一个刚性的单应性矩阵完成配准。为提高配准的精度,Apap将图像切割成无数多个小方块,对每个小方块的变换矩阵逐一估计。
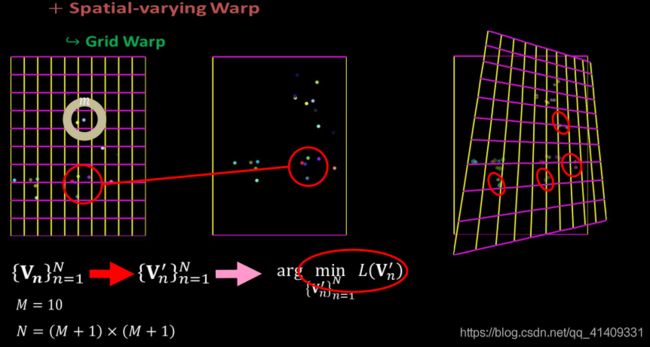
效果展示

Lowe’s算法
为了排除因为图像遮挡和背景混乱而产生的无匹配关系的关键点,SIFT的作者Lowe提出了比较最近邻距离与次近邻距离的SIFT匹配方式:取一幅图像中的一个SIFT关键点,并找出其与另一幅图像中欧式距离最近的前两个关键点,在这两个关键点中,如果最近的距离除以次近的距离得到的比率ratio少于某个阈值T,则接受这一对匹配点。因为对于错误匹配,由于特征空间的高维性,相似的距离可能有大量其他的错误匹配,从而它的ratio值比较高。显然降低这个比例阈值T,SIFT匹配点数目会减少,但更加稳定,反之亦然。
Lowe推荐ratio的阈值为0.8,但作者对大量任意存在尺度、旋转和亮度变化的两幅图片进行匹配,结果表明ratio取值在0. 4~0. 6 之间最佳,小于0. 4的很少有匹配点,大于0. 6的则存在大量错误匹配点,所以建议ratio的取值原则如下:
ratio=0.4:对于准确度要求高的匹配;
ratio=0.6:对于匹配点数目要求比较多的匹配;
ratio=0.5:一般情况下。
效果十分明显
由于这部分以前做过,当时使用的是C++和opencv库,所以这里给出的是C++的代码
#include "stdafx.h"
#include "highgui/highgui.hpp"
#include "opencv2/nonfree/nonfree.hpp"
#include "opencv2/legacy/legacy.hpp"
#include <iostream>
using namespace cv;
using namespace std;
void OptimizeSeam(Mat& img1, Mat& trans, Mat& dst);
typedef struct
{
Point2f left_top;
Point2f left_bottom;
Point2f right_top;
Point2f right_bottom;
}four_corners_t;
four_corners_t corners;
int main(int argc, char *argv[])
{
Mat image01 = imread("D:\\Univ2.jpg", 1); //右图
Mat image02 = imread("D:\\Univ3.jpg", 1); //左图
imshow("p2", image01);
imshow("p1", image02);
//灰度图转换
Mat image1, image2;
cvtColor(image01, image1, CV_RGB2GRAY);
cvtColor(image02, image2, CV_RGB2GRAY);
//提取特征点
SurfFeatureDetector Detector(2000);
vector<KeyPoint> keyPoint1, keyPoint2;
Detector.detect(image1, keyPoint1);
Detector.detect(image2, keyPoint2);
//特征点描述,为下边的特征点匹配做准备
SurfDescriptorExtractor Descriptor;
Mat imageDesc1, imageDesc2;
Descriptor.compute(image1, keyPoint1, imageDesc1);
Descriptor.compute(image2, keyPoint2, imageDesc2);
FlannBasedMatcher matcher;
vector<vector<DMatch> > matchePoints;
vector<DMatch> GoodMatchePoints;
vector<Mat> train_desc(1, imageDesc1);
matcher.add(train_desc);
matcher.train();
matcher.knnMatch(imageDesc2, matchePoints, 2);
cout << "total match points: " << matchePoints.size() << endl;
// Lowe's algorithm,获取优秀匹配点
for (int i = 0; i < matchePoints.size(); i++)
{
if (matchePoints[i][0].distance < 0.4 * matchePoints[i][1].distance)
{
GoodMatchePoints.push_back(matchePoints[i][0]);
}
}
Mat first_match;
drawMatches(image02, keyPoint2, image01, keyPoint1, GoodMatchePoints, first_match);
imshow("first_match ", first_match);
vector<Point2f> imagePoints1, imagePoints2;
for (int i = 0; i<GoodMatchePoints.size(); i++)
{
imagePoints2.push_back(keyPoint2[GoodMatchePoints[i].queryIdx].pt);
imagePoints1.push_back(keyPoint1[GoodMatchePoints[i].trainIdx].pt);
}
}
通过图割方法,自动选取拼接缝
二元组G=

如上图左。A,B是两幅图片,对应着左侧和右侧区域,他们的重叠区域是中间部分。这条曲线就是要查找的目标缝合线。如上图右。该图是重叠部分的简易带权有向图和最佳缝合线, 该缝合线就是用最大流计算而来的最小缝合线。权值的设置是搜索和查找缝合线的关键。求解最佳缝合线的过程就是在两幅图重叠部分找出像素灰度值之差最小的那组点,然后通过计算对边赋予权值以实现图的最小割。
根据Multi-Band Blending策略实现融合
融合两张图片最直接的可以将重叠部分进行加权融合,但这样往往效果很差,出现重影,如下图

这是两张图片拼接后的重叠部分,很明显可以看到井盖出现的重影。
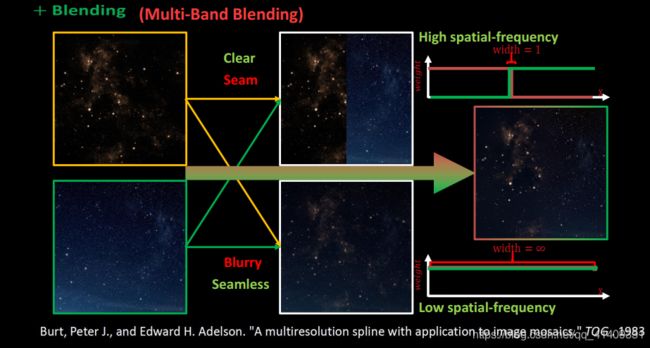
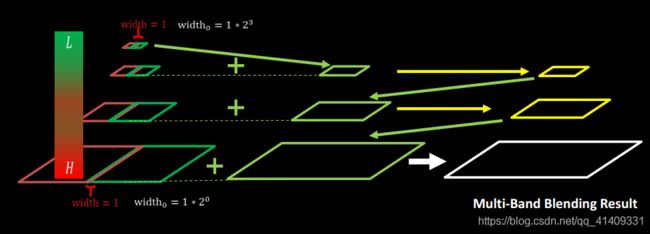
Multi-Band算法就是将图像分解为不同频带的分量之加和,图像的宏观特征在它的低频分量图里,而局域特征在高频分量图里。
基本流程:
- 计算输入图像的高斯金字塔
- 计算输入图像的拉普拉斯金字塔

- 将处于同一级的拉普拉斯金字塔进行融合。可以是简单的线性融合。
- 将高层的拉普拉斯金字塔依次扩展直至和源图像相同分辨率

- 将得到的图像依次叠加,则得到最终的输出图像。
实验结果
实现代码
from pylab import *
from numpy import *
from PIL import Image
# If you have PCV installed, these imports should work
from PCV.geometry import homography, warp
from PCV.localdescriptors import sift
"""
This is the panorama example from section 3.3.
"""
# set paths to data folder
featname = ['sift2/Univ'+str(i+1)+'.sift' for i in range(5)]
imname = ['image2/Univ'+str(i+1)+'.jpg' for i in range(5)]
# extract features and match
l = {}
d = {}
for i in range(5):
sift.process_image(imname[i],featname[i])
l[i],d[i] = sift.read_features_from_file(featname[i])
matches = {}
for i in range(4):
matches[i] = sift.match(d[i+1],d[i])
# visualize the matches (Figure 3-11 in the book)
for i in range(4):
im1 = array(Image.open(imname[i]))
im2 = array(Image.open(imname[i+1]))
figure()
sift.plot_matches(im2,im1,l[i+1],l[i],matches[i],show_below=True)
# function to convert the matches to hom. points
def convert_points(j):
ndx = matches[j].nonzero()[0]
fp = homography.make_homog(l[j+1][ndx,:2].T)
ndx2 = [int(matches[j][i]) for i in ndx]
tp = homography.make_homog(l[j][ndx2,:2].T)
# switch x and y - TODO this should move elsewhere
fp = vstack([fp[1],fp[0],fp[2]])
tp = vstack([tp[1],tp[0],tp[2]])
return fp,tp
# estimate the homographies
model = homography.RansacModel()
fp,tp = convert_points(1)
H_12 = homography.H_from_ransac(fp,tp,model)[0] #im 1 to 2
fp,tp = convert_points(0)
H_01 = homography.H_from_ransac(fp,tp,model)[0] #im 0 to 1
tp,fp = convert_points(2) #NB: reverse order
H_32 = homography.H_from_ransac(fp,tp,model)[0] #im 3 to 2
tp,fp = convert_points(3) #NB: reverse order
H_43 = homography.H_from_ransac(fp,tp,model)[0] #im 4 to 3
# warp the images
delta = 2000 # for padding and translation
im1 = array(Image.open(imname[1]), "uint8")
im2 = array(Image.open(imname[2]), "uint8")
im_12 = warp.panorama(H_12,im1,im2,delta,delta)
im1 = array(Image.open(imname[0]), "f")
im_02 = warp.panorama(dot(H_12,H_01),im1,im_12,delta,delta)
im1 = array(Image.open(imname[3]), "f")
im_32 = warp.panorama(H_32,im1,im_02,delta,delta)
im1 = array(Image.open(imname[4]), "f")
im_42 = warp.panorama(dot(H_32,H_43),im1,im_32,delta,2*delta)
figure()
imshow(array(im_42, "uint8"))
axis('off')
savefig("example1.png",dpi=300)
show()




