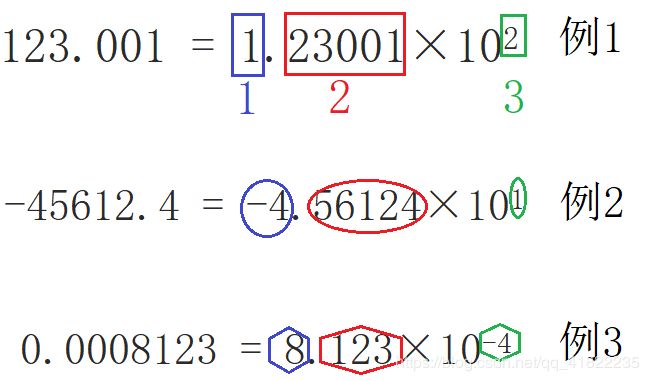float强转int

本文只讨论float转int的原理，如有不当之处，欢迎留言指出。交流学习。 

推荐阅读关于float转int的函数实现（非结构体实现版） 类型强转丢失精度的根源

目录

一、思路

1.1 十进制

1.2 二进制

1.3 处理棘手的符号位

1.4 小端模式

二、C语言实现

2.1 思路

2.2 利用结构体实现

2.3 利用内存拷贝函数memcpy实现

---

一、思路

1.1 十进制

大体和科学计数法（小数点前面只有1位，和用什么进制实现没有关系）别无二致。如果十进制：

图1 十进制下的科学计数法

从图1 我们可以看到， 对于科学计数法而言，小数点前面只有1位、小数点后面是有效位、以10为底数的幂有正有负有0。那么为了记录一个十进制数，我们需要记录四个要素：符号、小数点前的一位、有效位、指数。

1.2 二进制

类比到二进制，小数点前面一位一定是1，正如十进制小数点前面一位一定是1-9一样；那么我们只需记录符号、有效位以及指数。下面我们先举一个例子：-12,25展成float。注意：此处不要去想表示整型的原码反码补码那一套了。正如稍前讨论的那般，指数是有正负的，那如果不加某种手段，如何表示指数的正负呢？

1.3 处理棘手的符号位

IEEE二进制浮点数算术标准（ANSI/IEEE Std 754-1985）告诉我们一个很棒的解决办法：是这样做的，选取8bite用于表示指数部分（底数是2），有256种变化，既可以理解为0-255也可以理解为-128-127，取决于设计者是如何去解释的。而后者是非常好的，正指数和负指数都是127一人一半。所以不管实际指数是多少，一律加上127类似于加密过程；等到想把真实值取出来的时候，一律减去127类似于解密过程。

现在来演算一下-12.25如何展成float吧：

图2 -12.25展成float

最后我们才能大体看懂这张示意图：

图3 float类型结构示意图

1.4 小端模式

大端模式和小端模式的由来

二、C语言实现

2.1 思路

难点在于如何用一个变量去读出内存中存放的float类型的变量。最直接的办法就是按照float类型的结构去设计一个完全一致的结构体，更为巧妙的办法是将float类型的变量通过调用内存拷贝函数memcpy复制到unsigned long类型的变量中。这两种办法都能将float类型的变量取出，然后分别读取符号位、指数位、尾数有效位。

学无止境，下面分别讨论这两种思路的实现：

2.2 利用结构体实现

用到了位域的知识点：

图4 单词mantissa

结构体设计以及函数声明。

#include //printf()
#include //atof()

typedef struct FloatNode
{
    unsigned int mantissa : 23; //尾数部分
    unsigned int exponent : 8; //指数部分
    unsigned int sign : 1;  //符号位
}FloatNode;

int GetSign(const FloatNode *fn); //获取符号位
int GetExp(const FloatNode *fn); //获取指数部分
int Float_To_Int(float num); //类型强制转换

---

其他函数的实现

int GetSign(const FloatNode *fn) //获得符号位
{
    return fn->sign == 1 ? -1 : 1;
}

int GetExp(const FloatNode *fn) //获得指数位
{
    return (fn->exponent - 127); //根据IEEE754,减去127才是真正的指数位
}

int Float_To_Int(float num) //将float强转成int
{
    FloatNode *fn = (FloatNode*)#
    int exp = GetExp(fn);

    if(exp >= 0)
    {
        int mov = 23 - exp;
        int res = (fn->mantissa | 1<<23) >> mov;
        return res*GetSign(fn);
    }
    else
    {
        return 0;
    }
}

main主函数

int main(int argc, char* argv[])
{
    if(argc <= 1)
    {
        printf("%s\n", "Argument isn't enough.");
        return 0;
    }
    char *p = argv[1];
    float num = atof(p);
    int res = Float_To_Int(num);
    printf("转换之后的结果是：%d\n", res);
    return 0;
}

图5 linux下运行结果

2.3 利用内存拷贝函数memcpy实现

重要的话，浮点型没有移位运算，或者说，即使强行进行移位运算也是被当成整型对待而得到错误的结果。如果不用一个和float类型完全一致的结构体去读取，那么只能将float类型的数据放到unsigned类型中再进行操作。

实际上就是对float型的结构进行解析，尤要注意的是运算符的优先级，告诫本篇博客的博友们：不要止步于看懂，自己也要写一写。

库文件的引入及函数的声明：

#include //printf()
#include //memcpy()
#include //atof()

int getSign(unsigned num);      //获得符号位
int getExp(unsigned num);       //获得指数部分
int float2int(float ft);    //float强转为int

其他函数的实现

int getSign(unsigned num)       //获得符号位
{
    int sign = num & (1<<31);
    return sign == 0 ? 1 : -1; 
}

int getExp(unsigned num)        //获得指数部分
{
    int exp = 0;
    for(int i = 23; i < 31; ++i)
        exp |= (num & (1<>23) - 127;
    return exp;
}

int float2int(float ft) //float强转为int
{
    unsigned num;
    memcpy(&num, &ft, sizeof(float)); //将float数据完整地拷贝到unsigned中

    int exp = getExp(num); //获得float存储结构的指数部分
    if(exp < 0) //如果指数小于0的话，实际值肯定是0.***,故而强转之后就为0
    {
        return 0;
    }
    else
    {
        int res = num & ((1<<23)-1);  //保留mantissa 注意运算符的优先级
        res |= 1<<23;   //将小数点前的1补上
        res >>= (23-exp); //整数部分右移到合适位置
        return res*getSign(num);
    }
}

main主函数

int main(int argc, char * argv[])
{
    if(argc <= 1)
    {
        printf("augument is not enough.\n");
        return 0;
    }

    float ft = atof(argv[1]); //将字符串转化为同值的float
    int res = float2int(ft);
    printf("转换之后的结果是：%d\n", res);
    return 0;
}

运行结果：

图6 linux下运行结果