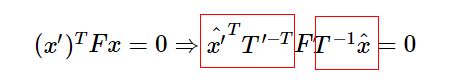计算机视觉——多视图几何

一、关于对极几何

1.1几个基本概念

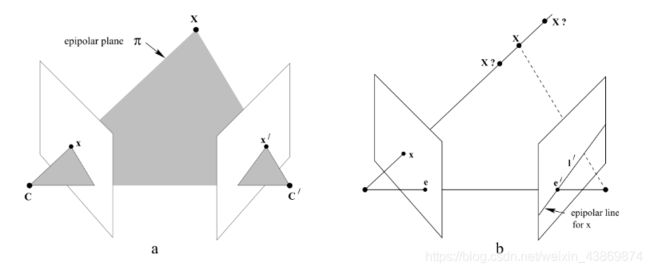
对极几何： 描述的是两幅视图之间的内在射影关系，与外部场景无关，只依赖于摄像机内参数和这两幅视图之间的相对位姿。
基线： 两个相机中心的连线CC’称为基线(如图a)。
对极点： 图（b）中e、e’是对极点，是基线与两个成像平面的交点，也就是两个相机在另一个成像平面上的像点
对极线： 是对极平面和成像平面的交线，所有的对极线都相交于极点。
对极面： 包含基线的平面（如图a的面xcc’）
对极约束： 在一幅图像中上的p点在另一幅图像中的对应点一定在基线I’上（如下图所示）

关于多视图几何基础知识
  由于以下本质矩阵（E）和基础矩阵（F）的推导计算，涉及矩阵的运算、秩、自由度等问题，关于这些基础知识，建议参考这位笔者的笔记SLAM基础知识补充：多视图几何，此笔记极其详细，推荐学习！

1.2本质矩阵（E）

1.2.1 作用

  用于描述空间中同一点在不同坐标系下的对应关系

1.2.2 求解推导

设平面内一点X，在以C为中心的坐标系中为p，在以C’为中心的坐标系中为p’(如下图所示)

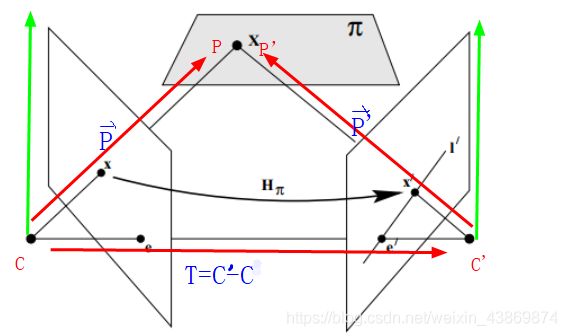
建立X点在C、C’坐标系下的关系，可得到如下方程

其中R为两图像的旋转关系，T为两图像的位移关系
又∵CX、XC’、C’C三线共面
因此有如下关系

其中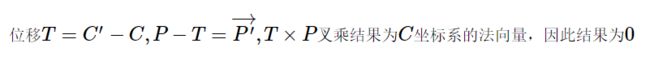
公式(1)移项得

将上式代入式子（2）得

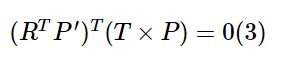
∵有
∴可得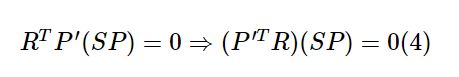
由式子（4）中

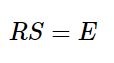
得到

1.2.3 本质矩阵的性质

1. 只有5个自由度，旋转矩阵R和平移矢量t各有3个自由度，由于是齐次矩阵再减去一个自由度
2. 本质矩阵仅依赖外部参数（Extrinsic Parameters) （R & T）决定

1.3基础矩阵（F）

1.3.1 作用

  用于描述两个像平面中的点的对应关系

1.3.2求解推导

主要思路为将空间中同一点不同坐标对应关系（即本质矩阵）变换为像平面中点的对应关系
∵X点投影到左平面为x,投影到右平面为x’（K，K’为相机的内参矩阵）
∴有


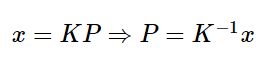
因此可得

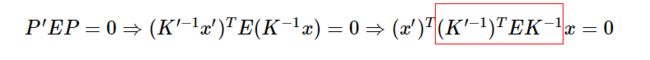
又∵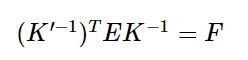
∴得

1.3.3基础矩阵的性质

• 基础矩阵是一个3*3且自由度为7的矩阵
• 基础矩阵的秩为2
• 对任意匹配点对 $x\leftrightarrow x$’ 均满足$x^{T}Fx’$=0

关于本质矩阵与基础矩阵自由度不同的问题
可参考这个网页为什么本质矩阵５自由度，基础矩阵７自由度，单应矩阵８自由度？

1.4八点算法求解基础矩阵（F）

  基础矩阵中有 3×3=9 个元素，由于尺度是任意的，所以至少需要7个点对应点7个方程。因为算法中需要 8 个对应点来计算基础矩阵 F，所以该算法叫做八点法。
  求解基础矩阵(F)的本质是：求解图片1中的一个点$x$与图片2中对应的点$x^{\prime }$应该满足什么样的约束。
主要求解如下：
  任给两幅图像的x和x’,由于每一组点的匹配提供了计算F系数的一个线性方程，当给定至少7 个点（基础矩阵F的秩为2），方程可计算出未知的基础矩阵F。
令



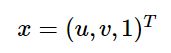
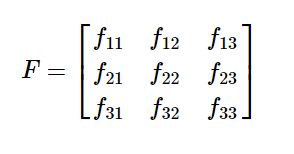
则有

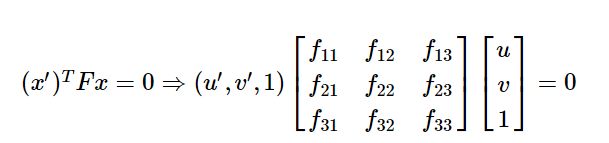
展开后为

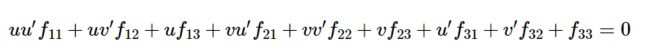
则有

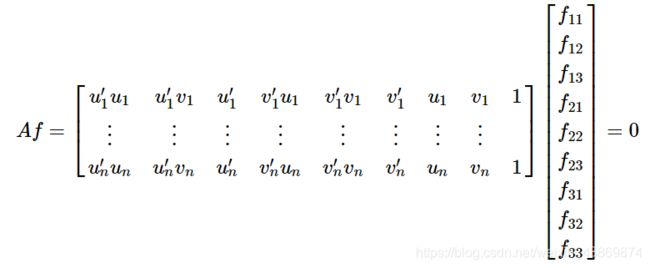
继续求解有两种解法
①直接求解参数法
  由$A^{T}A$的分解求解参数
②非线性优化法（主要用最小二乘法）
  由于点坐标存在噪声则矩阵$A$的自由度可能大于8（也就是等于9，由于A $A$是$n\times 9$的矩阵），故用最小二乘法。
  通过$SVD$分解来求解，$f$的解就是系数矩阵$A$最小奇异值对应的奇异向量,$A$的奇异值分解后$A=UD{V}^T$ 中矩阵 $V$的最后一列矢量,在满足$||f||=1$的约束使得$||Af||$最小化。

最后，进行8点算法前，应先对各列向量归一化处理，这样有助于提高解的稳定性和精度。

归一化八点算法求解方法如下：

1. 将图像坐标变换到合适的范围$\widehat{x_i}=T_{x_i}$,$\widehat{x_i^{\prime }}=T_{x_i^{\prime }}$，其中$T$和$T^{\prime }$ 是有平移和缩放组成的归一化变换
2. 根据变换后的坐标$\widehat{x_i}$,$\widehat{x_i^{\prime }}$,确定的系数矩阵$\hat{A}$的最小奇异值的奇异矢量,计算归一化举出矩阵$\hat{F}$
3. 解除归一化，令$F=T^{\prime T}\hat{F}T$
   

优点： 线性求解，容易实现，运行速度快
缺点： 对噪声敏感

---

二、求解图像之间的基础矩阵

代码：
主要思路：

• 利用opencv中的SIFT特征匹配
• 寻找两幅图的匹配特征点，
• 利用FLANN 匹配器（快速近似最近邻搜索算法）进行快速匹配
• 进行比值测试，去除错配（比值测试的意思是首先获取与A距离最近的点B[最近]和C[次近]，只有当B/C小于阈值[0.8]才被认为是匹配。）
• 得到匹配点列表后，利用cv.findFundamentalMat计算基础矩阵

retval, mask=cv.findFundamentalMat(points1, points2, method, ransacReprojThreshold, confidence, mask)

1. points1：从第一张图片开始的N个点的数组。点坐标应该是浮点数(单精度或双精度)。
2. points2：与点1大小和格式相同的第二图像点的数组。
3. method：计算基本矩阵的方法。
4. cv2.FM_7POINT for a 7-point algorithm. N=7
   cv2.FM_8POINT for an 8-point algorithm. N≥8
   cv2.FM_RANSAC （默认） for the RANSAC algorithm. N≥8
   cv2.FM_LMEDS for the LMedS algorithm. N≥8
5. ransacReprojThreshold：仅用于RANSAC方法的参数，默认3。它是一个点到极线的最大距离(以像素为单位)，超过这个点就被认为是一个离群点，不用于计算最终的基本矩阵。根据点定位、图像分辨率和图像噪声的准确性，可以将其设置为1-3左右。
6. confidence：仅用于RANSAC和LMedS方法的参数，默认0.99。它指定了一个理想的置信水平(概率)，即估计矩阵是正确的。
7. mask：输出，极外几何描述如下

import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt

img1 = cv.imread('data/mleft1.jpg', 0)  #图1
img2 = cv.imread('data/mright2.jpg', 0)  #图2
sift = cv.xfeatures2d.SIFT_create()
#SIFT特征匹配寻找特征点
kp1, des1 = sift.detectAndCompute(img1, None)
kp2, des2 = sift.detectAndCompute(img2, None)
# FLANN 匹配器
FLANN_INDEX_KDTREE = 1
index_params = dict(algorithm=FLANN_INDEX_KDTREE, trees=5)
search_params = dict(checks=50)
flann = cv.FlannBasedMatcher(index_params, search_params)
matches = flann.knnMatch(des1, des2, k=2)
good = []
pts1 = []
pts2 = []
# 比值检测，去除错配
for i, (m, n) in enumerate(matches):
    if m.distance < 0.8 * n.distance:
        good.append(m)
        pts2.append(kp2[m.trainIdx].pt)
        pts1.append(kp1[m.queryIdx].pt)

pts1 = np.int32(pts1)
pts2 = np.int32(pts2)
F, mask = cv.findFundamentalMat(pts1, pts2, cv.FM_LMEDS)
print(F)
# 只选择内点
pts1 = pts1[mask.ravel() == 1]
pts2 = pts2[mask.ravel() == 1]

2.1七点匹配点计算基础矩阵结果

（1）左右拍摄，极点位于图像平面上

（2）像平面接近平行，极点位于无穷远

（3）图像拍摄位置位于前后

2.2八点匹配点计算基础矩阵结果

（1）左右拍摄，极点位于图像平面上

（2）像平面接近平行，极点位于无穷远

（3）图像拍摄位置位于前后

2.3十点匹配点计算基础矩阵结果

（1）左右拍摄，极点位于图像平面上

（2）像平面接近平行，极点位于无穷远

（3）图像拍摄位置位于前后

分析：
  基础矩阵立体像对的两幅图像在拍摄时相互之间的空间几何关系（外参数）以及相机检校参数（内参数），包括旋转、位移、像主点坐标和焦距。因为F矩阵的秩为2，并且可以自由缩放（尺度化），所以只需7对同名点即可估算出F的值。
  由结果看看出， 同样的匹配点数，3组不同图片的基础矩阵，左右拍摄和前后拍摄得到的基础矩阵值大于平行拍摄。

---

三、画出极点和极线

3.1代码

#画出极点和极线
def drawlines(img1, img2, lines, pts1, pts2):
    r, c = img1.shape
    img1 = cv.cvtColor(img1, cv.COLOR_GRAY2BGR)
    img2 = cv.cvtColor(img2, cv.COLOR_GRAY2BGR)
    for r, pt1, pt2 in zip(lines, pts1, pts2):
        color = tuple(np.random.randint(0, 255, 3).tolist())
        x0, y0 = map(int, [0, -r[2] / r[1]])
        x1, y1 = map(int, [c, -(r[2] + r[0] * c) / r[1]])
        img1 = cv.line(img1, (x0, y0), (x1, y1), color, 1)
        img1 = cv.circle(img1, tuple(pt1), 5, color, -1)
        img2 = cv.circle(img2, tuple(pt2), 5, color, -1)
    return img1, img2
    
#在右图上找到对应得点，在左图上画线
lines1 = cv.computeCorrespondEpilines(pts2.reshape(-1, 1, 2), 2, F)
lines1 = lines1.reshape(-1, 3)
img5, img6 = drawlines(img1, img2, lines1, pts1, pts2)
#在左图上找到对应的点在右图画线
lines2 = cv.computeCorrespondEpilines(pts1.reshape(-1, 1, 2), 1, F)
lines2 = lines2.reshape(-1, 3)
img3, img4 = drawlines(img2, img1, lines2, pts2, pts1)
plt.subplot(121), plt.imshow(img5)
plt.subplot(122), plt.imshow(img3)
plt.show()

3.2结果

3.2.1左右拍摄，极点位于图像平面上

七个匹配点


八个匹配点

十个匹配点


分析：
  图片拍摄角度为左，右各拍摄一张，两图中极线呈倾斜，图中显示出了两图中找到的特征点，根据一图中的特征点，找到另一图中匹配的特征点，由结果可以看出7个匹配点和10个匹配点匹配出的基础矩阵是相同的，画出的两图极线也是相同的。但8个匹配点时，两图出现了极线交于1个极点，猜测是受噪点影响。

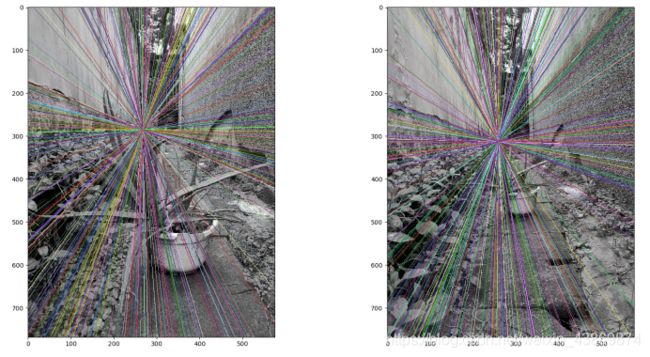
3.2.2像平面接近平行，极点位于无穷远

七个匹配点

八个匹配点


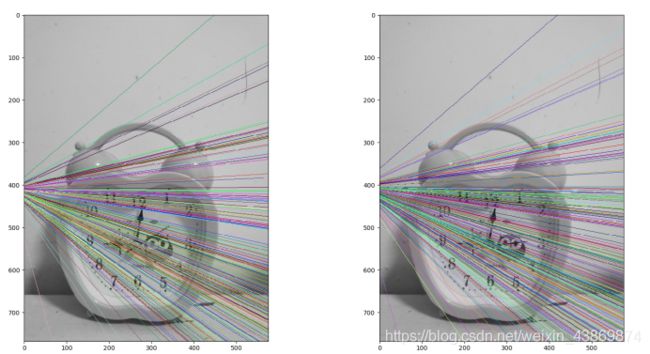
十个匹配点


分析：
  可以看出7和10个匹配点图中极线与x轴平行，两图片相机中心的连线与x轴平行，即基线与两个成像平面平行，因而没有极点。
  8个匹配点时，两图片出现了倾斜的极线，并未与x轴平行，猜测是因为受噪声点影响。
  另外这组图片拍摄时，要求较高。拍摄多组图片绘制极线都没有得到理想的与x抽平行的极线，总结经验是拍摄时两张图要保持相机在同一水平线上，才能得到理想的极线。

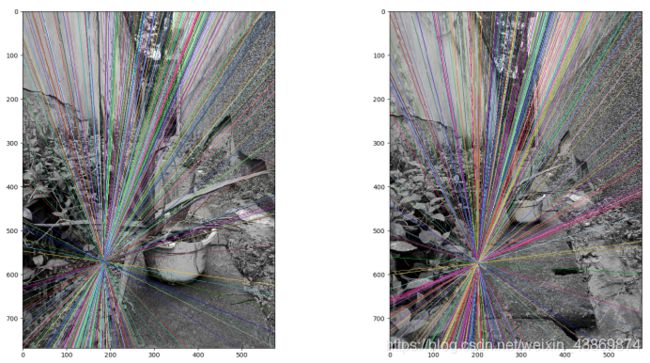
3.2.3图像拍摄位置位于前后

七个匹配点


八个匹配点

十个匹配点


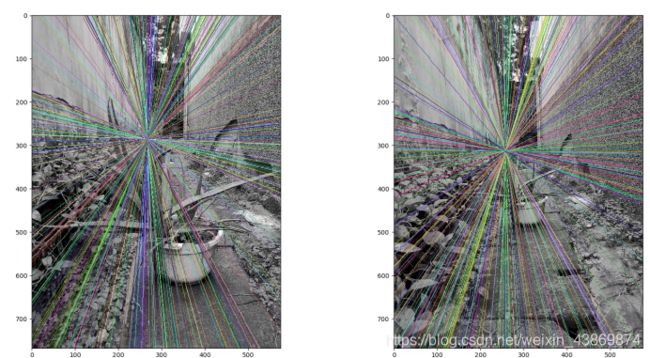
分析：
  由极线图可以看出拍摄位置前后的图片，极线交于一点，左右两图对极点位置相同，但取不同个数匹配点极线的交点位置并不相同。
  极线交于一点，是因为两图像为相机前后平移拍摄，由相机坐标系转为图像坐标系（三维->二维）相机前后的位置信息丢失，因而两图片的图像坐标系是相同的，左右两图对极点位置相同。

---

四、小结

• 内参矩阵 K是针对单相机的，通过焦距和主点位置直接表示了相机坐标系和图像坐标系之间的关系，如果考虑镜头的畸变，还需要有畸变系数，如果图像传感器有倾斜，还需要有倾斜因子。
• 本质矩阵 E根据左右相机的R（旋转）、T（位移）关系，表示了对极线关系，本质矩阵是左右摄像机坐标系之间的关系，求解本质矩阵的核心是求左右相机的R（旋转）、T（位移）。给定两个已标定相机的相对位置关系，E即被确定。
• 基础矩阵F是图像坐标系下的，结合了本质矩阵和内参矩阵，直接反应左右空间中的点在图像坐标系下对应关系。给定了两个相机的相对位置关系和相机内参，F即被确定。
• 本质矩阵 E可以理解为是基础矩阵F的一个特例，关系表达为$(K^{\prime -1}{)}^{T}E{K}^{-1}=F$