【MATLAB】解偏微分方程(显式法、Crank-Nicholson隐式法等)
之一:【MATLAB】逐步搜索法、二分法、比例求根法、牛顿法、弦截法求方程的根
之二:【MATLAB】欧拉法、2阶R-K法、4阶R-K法、预测-校正法(M-S法、A-M法)、有限差分法 解常微分方程
本文为《数值计算方法》的作业之三
未完成
5、显式法、Crank-Nicholson隐式法(抛物型偏微分方程)
上图疑似有误,应为 Crank-Nicholson 隐式法
边值为u
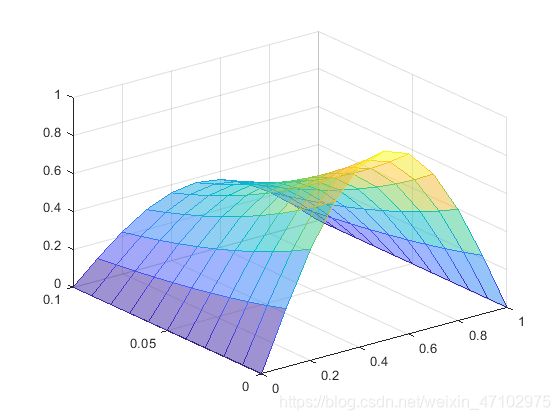
显式法
% 显式法(抛物型偏微分方程)
clear
% du d^2u
% --- = ------
% dt dx^2
% u(t,x_start) = g_1(t)
% u(t,x_end) = g_2(t)
% u(t_start,x) = f(x)
g_1 = @(t) 0;
g_2 = @(t) 0;
f = @(x) sin(pi .* x);
% △x = h △t = k
k = 0.01;
h = 0.1;
% u j-i t-x k-h
t_start = 0;
t_end = 0.1;
x_start = 0;
x_end = 1;
u = zeros(t_end/k+1,x_end/h+1);
r = k/(h.^2);
for j = 1:t_end/k+1
t = (j-1)*k;
for i = 1:x_end/h+1
x = (i-1) * h;
if j == 1
u(j,i) = f(x);
elseif i == 1
u(j,i) = g_1(t);
elseif i == x_end/h+1
u(j,i) = g_2(t);
else
u(j,i) = r*u(j-1,i-1)+(1-2*r)*u(j-1,i)+r*u(j-1,i+1);
end
end
end
surf(x_start:h:x_end,t_start:k:t_end,u,'FaceAlpha',0.5,'EdgeColor','interp')
Crank-Nicholson隐式法
此图与上一张图并不一样
% Crank-Nicholson 隐式法 (抛物型偏微分方程)
clear
% du d^2u
% --- = ------
% dt dx^2
% u(t,x_start) = g_1(t)
% u(t,x_end) = g_2(t)
% u(t_start,x) = f(x)
g_1 = @(t) 0;
g_2 = @(t) 0;
f = @(x) sin(pi .* x);
% △x = h △t = k
k = 0.01;
h = 0.1;
% u j-i t-x k-h
t_start = 0;
t_end = 0.1;
x_start = 0;
x_end = 1;
u = zeros(t_end/k+1,x_end/h+1);
r = k/(h.^2);
n = x_end/h+1;
for j = 1:t_end/k+1
t = (j-1)*k;
% Ax = B
A = zeros(n-2,n-2);
B = zeros(n-2,1);
u(j,1) = g_1(t);
u(j,n) = g_2(t);
for i = 2:n-1
x = (i-1) * h;
if j == 1
u(j,i) = f(x);
else
B(i-1) = r*u(j-1,i-1) + (2-2*r)*u(j-1,i) + r*u(j-1,i+1);
if i == 2
A(i-1,1:2) = [2+2*r,-r];
B(i-1) = B(i-1) + r*u(j,i-1);
elseif i == n - 1
A(i-1,end-1:end) = [-r,2+2*r];
B(i-1) = B(i-1) + r*u(j,i+1);
else
A(i-1,i-2:i) = [-r,2+2*r,-r];
end
end
end
if j ~= 1
u(j,2:end-1) = (A\B)';
end
end
surf(x_start:h:x_end,t_start:k:t_end,u,'FaceAlpha',0.5,'EdgeColor','interp')
边值为∂u
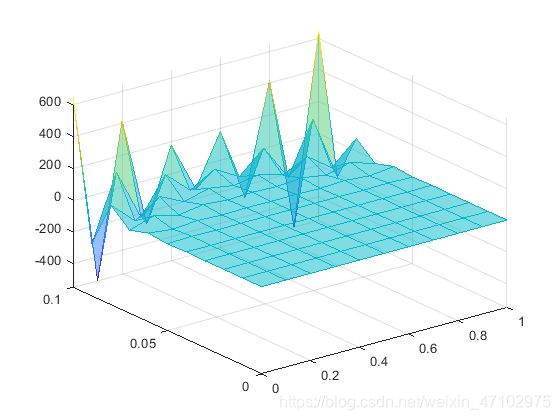
- 显式法的解
t的增大使解愈发异常,目前不太清楚原因
% 显式法(抛物型偏微分方程)
% **此部分代码疑似有误**
clear
% du d^2u
% --- = ------
% dt dx^2
% du(t,x_start)/dx = u(t,x_start)
% du(t,x_end)/dx = -u(t,x_end)
% u(t_start,x) = f(x)
f = @(x) 1;
% △x = h △t = k
k = 0.01;
h = 0.1;
% u j-i t-x k-h
t_start = 0;
t_end = 0.1;
x_start = 0;
x_end = 1;
u = zeros(t_end/k+1,x_end/h+1);
r = k/(h.^2);
for j = 1:t_end/k+1
t = (j-1)*k;
for i = 1:x_end/h+1
x = (i-1) * h;
if j == 1
u(j,i) = f(x);
elseif i == 1
u(j,i) = u(j-1,i) + 2*r*(u(j-1,i+1)-(1+h)*u(j-1,i));
elseif i == x_end/h+1
u(j,i) = u(j-1,i) + 2*r*(u(j-1,i-1)-(1+h)*u(j-1,i));
else
u(j,i) = r*u(j-1,i-1)+(1-2*r)*u(j-1,i)+r*u(j-1,i+1);
end
end
end
surf(x_start:h:x_end,t_start:k:t_end,u,'FaceAlpha',0.5,'EdgeColor','interp')
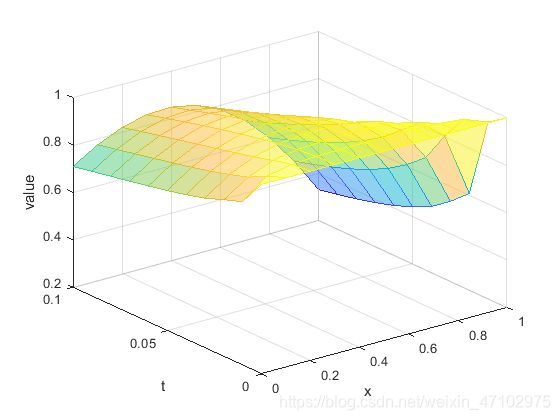
- 另一个同学的解法:
a = [4.2 -2 0 0 0 0 0 0 0 0 0
-1 4 -1 0 0 0 0 0 0 0 0
0 -1 4 -1 0 0 0 0 0 0 0
0 0 -1 4 -1 0 0 0 0 0 0
0 0 0 -1 4 -1 0 0 0 0 0
0 0 0 0 -1 4 -1 0 0 0 0
0 0 0 0 0 -1 4 -1 0 0 0
0 0 0 0 0 0 -1 4 -1 0 0
0 0 0 0 0 0 0 -1 4 -1 0
0 0 0 0 0 0 0 0 -1 4 -1
0 0 0 0 0 0 0 0 0 -2 4.2];
b = [
1.8
2
2
2
2
2
2
2
2
2
2];
e = zeros(11,1)
for i = 1:10
b = a\b;
e = [e,b];
b = [
2*b(2)-0.2*b(1)
b(1)+b(3)
b(2)+b(4)
b(3)+b(5)
b(4)+b(6)
b(5)+b(7)
b(6)+b(8)
b(7)+b(9)
b(8)+b(10)
b(9)+b(11)
b(10)-0.2*b(11)];
end
E = e;
e(:,1) = 1;
e;
ee = e';
X = 0:0.1:1;
T = 0:0.01:0.1;
surf(X,T,ee,'FaceAlpha',0.5,'EdgeColor','interp')
xlabel('x')
ylabel('t')
zlabel('value')
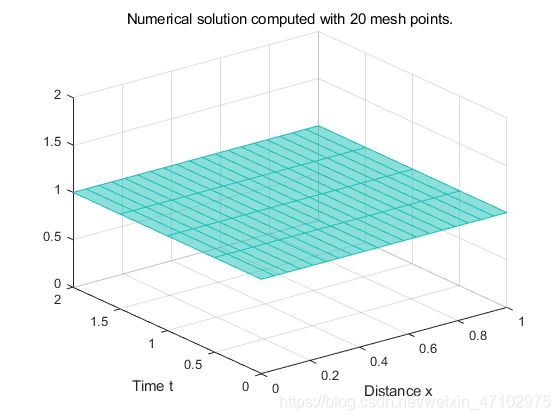
- 以通用方法求解(pdepe)
% 通用方法
m = 0;
x = linspace(0,1,20);
t = linspace(0,2,5);
sol = pdepe(m,@pdex1pde,@pdex1ic,@pdex1bc,x,t);
% Extract the first solution component as u.
u = sol(:,:,1);
% A surface plot is often a good way to study a solution.
surf(x,t,u,'FaceAlpha',0.5,'EdgeColor','interp')
title('Numerical solution computed with 20 mesh points.')
xlabel('Distance x')
ylabel('Time t')
function [c,f,s] = pdex1pde(x,t,u,DuDx)
c = 1;
f = DuDx;
s = 0;
end
function u0 = pdex1ic(x)
u0 = 1;
end
function [pl,ql,pr,qr] = pdex1bc(xl,ul,xr,ur,t)
pl = 0;
ql = 1;
pr = 0;
qr = -1;
end
#6、双曲型偏微分方程
#7、椭圆型偏微分方程
未完成