ACM图论部分__无向图的割点，桥的求解

1. 无向图的割点求法：

利用Tarjan算法思想，若一个点为割点，那么只存在两种情况：

（1）该点是根节点，且有两个以上子节点

（2）该点不上根节点，但是该点的低位数大于等于DFS数

低位数的定义：从该顶点v出发，只用最多一条回头边，沿有向边能走到的顶点中DFS数最小值。

DFS数：DFS遍历中的遍历顺序。

低位数L(v)的两种情况：
（1）没用上回头边，则能走到的DFS数最小的的顶点就是该点自身，对应的路是一个顶点构成的平凡的路。此时L(v)=DFN(v)。

（2）用了回头边，则一定是最后一条边是回头边，走到一个DFS数更小的顶点。此时L(v)<=DFN(v)。

下面直接给出代码：

#include 
#include 
#include 
#include 
using namespace std;
int e[100][100],m,root,n;
int num[100],low[100],flag[100],index=0;//index用于DFS数的递增
void cutPoint(int cur,int father)
{
    int child=0,i,j;
    index++;//每递归一次就自动增加1
    num[cur]=index;
    low[cur]=index;//开始时低位数与DFS遍历时间相同
    for(i=1;i<=n;i++)
    {
        if(e[cur][i]==1)
        {
            if(num[i]==0)//表明还没有访问过
            {
                child++;
                cutPoint(i,cur);//递归DFS
                low[cur]=min(low[i],low[cur]);//根据前面的递归，看是否可以找出最小的时间
                if(cur!=root&&low[cur]>=num[cur])
                {
                    flag[cur]=1;//表明它是割点，用flag标记
                }
                if(cur==root&&child>=2)//根节点必须有两个以上子节点
                {
                    flag[cur]=1;
                }
            }
            else if(i!=father)
            {
                low[cur]=min(low[cur],num[i]);//如果当前的点能回到更低的点，则应该马上改变它的低位数，因为后续点可能回不到这么低的点，下面给出图例说明
            }
        }


    }


}
int main()
{
    int i,j,x,y;
    memset(flag,0,sizeof(flag));
    memset(low,0,sizeof(low));
    memset(num,0,sizeof(num));
    cin>>n>>m;
    memset(e,0,sizeof(e));
    for(i=1;i<=m;i++)
    {
        cin>>x>>y;
        e[x][y]=1;
        e[y][x]=1;//无向图必须两边都设为连通
    }
    root=1;
    cutPoint(1,root);
    for(i=1;i<=n;i++)
    {
        if(flag[i]==1)//flag用于标记是否是割点
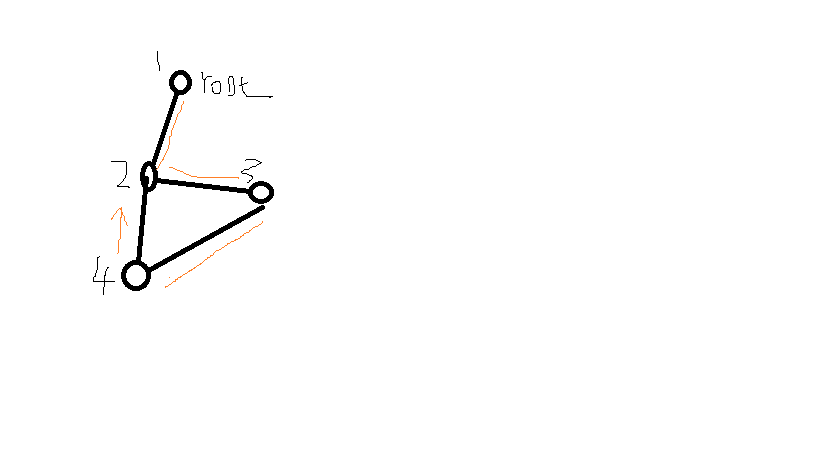
            cout<

下面给出图例：

如上图所示，当cutPoint从3到4时，我们将以4位cur，3位father进行递归,当我们递归时，可以发现2,4是连通的且2不是4的father，但是2的DFS数，明显更低，所以需要立刻更新。

2. 无向图的桥算法：

桥（割边）的定义：在无向图中删除掉一条边，那么这个图不在连通，则叫 这条边为桥

割边的求法与割点的求法非常类似，下面直接给出代码：

void cutEdge(int cur,int father)//传入两个参数，当前顶点编号和父节点的编号
{
    int child=0,i,j;//用child记录当前顶点的子节点个数
    index++;//时间戳递增
    num[cur]=index;//当前顶点的时间戳
    low[cur]=index;//当前顶点能够访问到最早的时间戳，是它本身
    for(i=1;i<=n;i++)//枚举与当前顶点cur有相邻边的顶点
    {
        if(e[cur][i]==1)
        {
            if(num[i]==0)//如果时间戳为0，说明还没有访问过
            {
                //child++;
                cutEdge(i,cur);//继续往下深度优先遍历
                low[cur]=Min(low[cur],low[i]);//更新当前顶点能够访问到最早顶点的时间戳
                if(low[i]>num[cur])//这时不能取等于，因为一条边的两个点肯定不同
                {
                    cout<

该博客为原创博客，可以转载但需要注明出处，谢谢合作！