最小路径覆盖

花了好长时间，用于找了几篇能看懂的最小路径覆盖。

 

定义：通俗点将，就是在一个有向图中，找出最少的路径，使得这些路径经过了所有的点。

最小路径覆盖分为最小不相交路径覆盖和最小可相交路径覆盖。

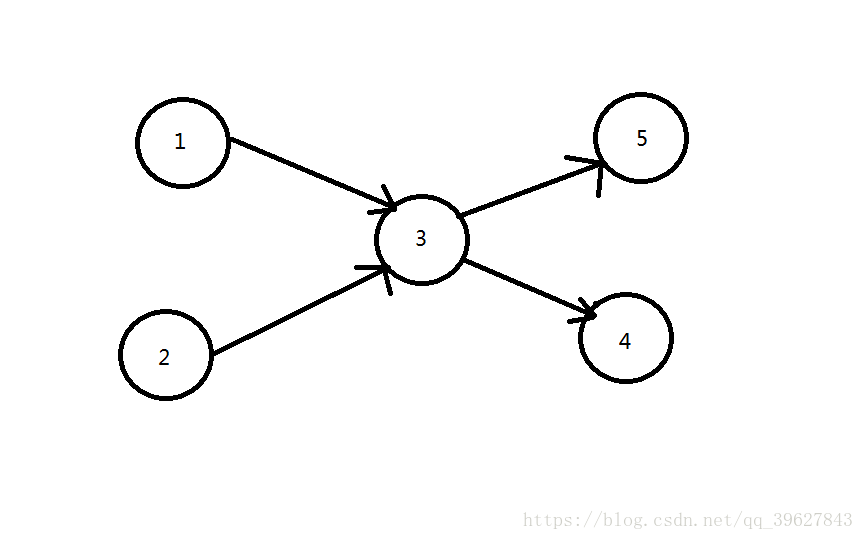
最小不相交路径覆盖：每一条路径经过的顶点各不相同。如图，其最小路径覆盖数为3。即1->3>4，2，5。

最小可相交路径覆盖：每一条路径经过的顶点可以相同。如果其最小路径覆盖数为2。即1->3->4，2->3>5。

特别的，每个点自己也可以称为是路径覆盖，只不过路径的长度是0。

 

大家要仔细想想上面的解释啊，这已经是我找到的最浅显的了。

而且一定要知道有这两种最小路径覆盖。

然后如果大家不知道匈利亚算法的，一定要去看看，还是比较简单的，就是一个dfs，连我都看的懂。

下面地址是关于匈利亚算法的详解，带图解，易懂

https://blog.csdn.net/Arabic1666/article/details/79824390

DAG的最小不相交路径覆盖

算法：把原图的每个点V拆成VxVx和VyVy两个点，如果有一条有向边A->B，那么就加边Ax−>ByAx−>By。这样就得到了一个二分图。那么最小路径覆盖=原图的结点数-新图的最大匹配数。

证明：一开始每个点都是独立的为一条路径，总共有n条不相交路径。我们每次在二分图里找一条匹配边就相当于把两条路径合成了一条路径，也就相当于路径数减少了1。所以找到了几条匹配边，路径数就减少了多少。所以有最小路径覆盖=原图的结点数-新图的最大匹配数。

因为路径之间不能有公共点，所以加的边之间也不能有公共点，这就是匹配的定义。

说的拆点这么高深，其实操作起来超级超级简单，甚至没有操作。

简单的来说，每个顶点都能当成二分图中作为起点的顶点。

至于为什么答案是 n-ans，我谈谈我的理解

用dfs求的ans表示的意思是匹配数，换句话说，就是一条路连着的路径上的点的个数-1

比如说这个图，我们用匈牙利算法，遍历每个点，发现1、3点可行，可匹配，而2、4、5都不能行。

如果我们单纯考虑1->3->5这条路径，有三个点，然后有两个点匹配了，我们用3减去2，就得到了1，这个1就是一个路径数，需要用1条路径来覆盖，再对剩下的2、4考虑，分别都需要一条路径来覆盖，因为2-0=0，2是顶点个数，0是匹配数。

所以，对于每条分路径，我们需要 v-cnt的路径来覆盖，最后将每个分路径合起来，我们得到n-cnt。

例题：POJ1422

 

//
//  main.cpp
//  POJ1422最小不想交路径覆盖


#include 
#include 
#include 
#include 
using namespace std;
const int N = 200 + 10;
vector g[N];
int cy[N];
bool vis[N];
bool dfs(int u)
{
    for(int i=0; i

 

 

DAG的最小可相交路径覆盖

算法：先用floyd求出原图的传递闭包，即如果a到b有路径，那么就加边a->b。然后就转化成了最小不相交路径覆盖问题。

证明：为了连通两个点，某条路径可能经过其它路径的中间点。比如1->3->4，2->4->5。但是如果两个点a和b是连通的，只不过中间需要经过其它的点，那么可以在这两个点之间加边，那么a就可以直达b，不必经过中点的，那么就转化成了最小不相交路径覆盖。

上面的解释很不错，点个赞！

题目：POJ2594

//
//  main.cpp
//  POJ2594最小可相交路径覆盖
//
//  Created by beMaster on 16/4/8.
//  Copyright © 2016年 beMaster. All rights reserved.
//

#include 
#include 
#include 
#include 
using namespace std;
const int N = 500 + 10;
bool dis[N][N];
bool vis[N];
int cy[N];
void floyd(int n){
    for(int i=1;i<=n;++i)
        for(int j=1;j<=n;++j)
            for(int k=1;k<=n;++k)
                if(dis[i][k] && dis[k][j])//传递可达性
                    dis[i][j] = true;
}
bool dfs(int u, int n){
    for(int i=1;i<=n;++i){
        if(!vis[i] && dis[u][i]){
            vis[i] = true;
            if(cy[i]==-1 || dfs(cy[i], n)){
                cy[i] = u;
                return true;
            }
        }
    }
    return false;
}
int solve(int n){
    int cnt = 0;
    memset(cy,-1,sizeof(cy));
    for(int i=1;i<=n;++i){
        memset(vis,0,sizeof(vis));
        cnt += dfs(i, n);
    }
    return n - cnt;
}
int main( ) {
    int n,m;
    int a,b;
    while(scanf("%d%d",&n,&m),n+m){
        for(int i=1;i<=n;++i)
            for(int j=1;j<=n;++j)
                dis[i][j] = false;
        for(int i=1;i<=m;++i){
            scanf("%d%d",&a,&b);
            dis[a][b] = true;
        }
        floyd(n);
        int ans = solve(n);
        printf("%d\n",ans);
    }
    return 0;
}

 

做完这两道例题，可以做做我拉的题目啊，欢迎欢迎

https://vjudge.net/contest/249592#problem