专题·并查集【including 并查集基础，村村通，带权并查集，银河英雄传说，扩展域

初见安~这里是一个差点被遗忘了的并查集专题：）

并查集

顾名思义——并查集，就是合并，搜查集合。其本质意义为：

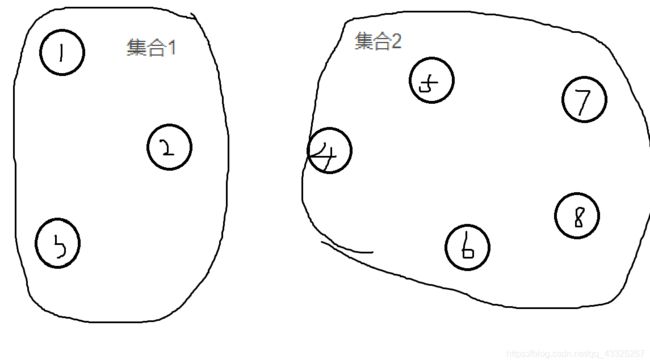
有n个集合的数，我们为了区别这几个集合，每个集合选择一个数作为代表，看某两个数是否在同一集合中，则只需看它们所在集合的代表数是否相同。

如果还没理解的话：

 

则我们可以设1为集合1的代表，4为集合2的代表。

在数组fa（father）中就可以存x点的所在集合代表：

看两个点是否在同一集合中，只要看两点的fa是否一样即可。

 

然而——

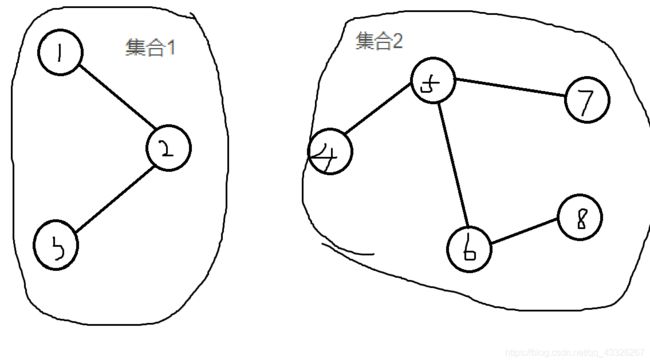
多数情况下我们是不可能一开始就确定每个点直属的集合的，往往是一种间接的关系。比如在上图中，实际情况可以是：

 

但我们仍然知道，1、2、3三个点是在同一集合里的。所以这时候我们就需要一个并查集专用函数之一：get操作来找点x真正的所在集合的代表点。

由上方情况我们可以得知：一个点如果它本身就是该集合的代表点，会有fa[ x ] = x。同理，就有了以下操作：

int get(int x)
{
	if(fa[x]==x) return x;//已经到了这个集合的代表节点，返回即可。
	return get(fa[x]);//否则继续递归找其父节点。
}

大致就是这个样子了：

当然，每个点在连边之前各自的根节点就是它自己，初始化为fa[ x ] = x;

所以有时我们会发现：递归的层数有可能会很大，甚至有时候如果在无向图中知道a、b相连，fa存fa[ a ] = b或者fa[ b ] = a都有可能判定的时候会出现有两个点的根连不到一块儿去的情况。即设a本就在集合1中，fa[ a ] = b后本应将b拉入集合1，却变成了a、b点在外单独成立一个集合的状态。所以我们在存fa的时候，存的是点的根节点相连。即

这就是并查集的正常操作了：）用到并查集的算法：最小生成树·Kruskal

---

下面我们来看一个例题：【这里是传送门：洛谷P1536

题目描述

某市调查城镇交通状况，得到现有城镇道路统计表。表中列出了每条道路直接连通的城镇。市政府“村村通工程”的目标是使全市任何两个城镇间都可以实现交通（但不一定有直接的道路相连，只要相互之间可达即可）。请你计算出最少还需要建设多少条道路？

输入格式：

 

每个输入文件包含若干组测试测试数据，每组测试数据的第一行给出两个用空格隔开的正整数，分别是城镇数目N（N<1000）和道路数目M；随后的M行对应M条道路，每行给出一对用空格隔开的正整数，分别是该条道路直接相连的两个城镇的编号。简单起见，城镇从1到N编号。

注意：两个城市间可以有多条道路相通。例如：

3 3 1 2 1 2 2 1 这组数据也是合法的。当N为0时，输入结束。

输出格式：

对于每组数据，对应一行一个整数。表示最少还需要建设的道路数目。

 

输入样例#1：

4 2
1 3
4 3
3 3
1 2
1 3
2 3
5 2
1 2
3 5
999 0
0

输出样例#1：

1
0
2
998

 

题解：

这是一个很基础的纯并查集操作题：已有的边全部连上，可以将图划分为n个互不连通集合，看有多少个集合就需要再连多少个-1条边来把它们连起来。

下面是代码及详解——

#include
using namespace std;

int f[2000];//fa数组
int get(int x)
{
    if(f[x]==x) return x;
    return get(f[x]);
}

int main()
{
    register int m,n,a,b,ans=0;
    while(scanf("%d",&n))
    {
        if(n==0) return 0;//读入完毕
        cin>>m;
        ans=0;
        for(register int i=1;i<=n;i++)
            f[i]=i;//初始化
            
        for(register int i=1;i<=m;i++)
        {
            cin>>a>>b;
            f[get(a)]=get(b);//存图连边
        }
        
        for(register int i=1;i<=n;i++)
        {
            if(f[i]==i) ans++;//有多少个根节点就是有多少个集合
        }
        cout<

带权并查集

并查集形如一棵树，而带权并查集就是这棵树上的边有权值。

好像这么说没什么用……直接上例题。

银河英雄传说

这里是洛谷传送门：洛谷P1196

题目描述

公元五八○一年，地球居民迁至金牛座α第二行星，在那里发表银河联邦创立宣言，同年改元为宇宙历元年，并开始向银河系深处拓展。

宇宙历七九九年，银河系的两大军事集团在巴米利恩星域爆发战争。泰山压顶集团派宇宙舰队司令莱因哈特率领十万余艘战舰出征，气吞山河集团点名将杨威利组织麾下三万艘战舰迎敌。

杨威利擅长排兵布阵，巧妙运用各种战术屡次以少胜多，难免恣生骄气。在这次决战中，他将巴米利恩星域战场划分成3000030000列，每列依次编号为1, 2, …,300001,2,…,30000。之后，他把自己的战舰也依次编号为1, 2, …, 300001,2,…,30000，让第ii号战舰处于第ii列(i = 1, 2, …, 30000)(i=1,2,…,30000)，形成“一字长蛇阵”，诱敌深入。这是初始阵形。当进犯之敌到达时，杨威利会多次发布合并指令，将大部分战舰集中在某几列上，实施密集攻击。合并指令为M_{i,j}Mi,j​，含义为第i号战舰所在的整个战舰队列，作为一个整体（头在前尾在后）接至第j号战舰所在的战舰队列的尾部。显然战舰队列是由处于同一列的一个或多个战舰组成的。合并指令的执行结果会使队列增大。

然而，老谋深算的莱因哈特早已在战略上取得了主动。在交战中，他可以通过庞大的情报网络随时监听杨威利的舰队调动指令。

在杨威利发布指令调动舰队的同时，莱因哈特为了及时了解当前杨威利的战舰分布情况，也会发出一些询问指令：C_{i,j}Ci,j​。该指令意思是，询问电脑，杨威利的第ii号战舰与第jj号战舰当前是否在同一列中，如果在同一列中，那么它们之间布置有多少战舰。

作为一个资深的高级程序设计员，你被要求编写程序分析杨威利的指令，以及回答莱因哈特的询问。

最终的决战已经展开，银河的历史又翻过了一页。

输入格式：

第一行有一个整数T(1 \le T \le 500,000)T(1≤T≤500,000)，表示总共有TT条指令。

以下有TT行，每行有一条指令。指令有两种格式：

M_{i,j}Mi,j​ ：ii和jj是两个整数(1 \le i,j \le 30000)(1≤i,j≤30000)，表示指令涉及的战舰编号。该指令是莱因哈特窃听到的杨威利发布的舰队调动指令，并且保证第ii号战舰与第jj号战舰不在同一列。

C_{i,j}Ci,j​ ：ii和jj是两个整数(1 \le i,j \le 30000)(1≤i,j≤30000)，表示指令涉及的战舰编号。该指令是莱因哈特发布的询问指令。

输出格式：

依次对输入的每一条指令进行分析和处理：

如果是杨威利发布的舰队调动指令，则表示舰队排列发生了变化，你的程序要注意到这一点，但是不要输出任何信息；

如果是莱因哈特发布的询问指令，你的程序要输出一行，仅包含一个整数，表示在同一列上，第ii号战舰与第jj号战舰之间布置的战舰数目。如果第ii号战舰与第jj号战舰当前不在同一列上，则输出-1−1。

输入样例#1： 

4
M 2 3
C 1 2
M 2 4
C 4 2

输出样例#1： 

-1
1

题解

这就是一个典型的边带权并查集。用并查集，如果我们不路径压缩的话，那么一直递归然后计数即可。但是看到n和m的范围就很明显不能这么做，并且一定要路径压缩。所以我们首先要多开一个数组d来维护点x到其祖先的距离。路径压缩的时候x的距离就是fa[x]的距离+1。那么在merge边的时候也不是简单连根了，还要维护接在后面的点的距离，所以我们还要存各个并查集的大小size。

下面上代码及详解——

#include
#define maxn 500005
using namespace std;
int n, a, b;
int size[maxn], d[maxn], fa[maxn];
int get(int x)
{
    if(fa[x] == x) return x;
    int root = get(fa[x]);
    d[x] += d[fa[x]];//路径压缩，更新距离
    return fa[x] = root;
}

void merge(int x, int y)
{
    x = get(x), y = get(y);
    fa[x] = y, d[x] = size[y];//连边，维护距离
    size[y] += size[x];//维护根节点大小即可，后面的节点会在后期路径压缩时更新
}

int main()
{
    scanf("%d", &n);
    char op;
    for(int i = 1; i <= maxn; i++)
        fa[i] = i, size[i] = 1;//初始化一定要更新size，否则d会爆0
        
    while(n--)
    {
        cin >> op;
        scanf("%d%d", &a, &b);
        if(op == 'M') merge(a, b);
        else
        {
            int u = get(a), v = get(b);
            if(u == v) printf("%d\n", abs(d[a] - d[b]) - 1);
            else puts("-1");
        }
    }
}

扩展域并查集

这个直接看例题就很清晰了【抱歉需要中转一下：NOI2001 食物链

迎评：）

——End——