noip 2016 做题记录
玩具谜题
简单模拟,主要判断当前小人的方向与操作方向的异或值,若为1则顺时针移动,否则逆时针移动。
#include换教室
首先用floyd处理出两点之间的距离,且因为有重边,所以在读入时要进行判断。
容易想到用dp来计算期望。f[i][j][1/0]表示到 i 时间时,已经申请更换了 j 个教室,第 i 个时间段是否申请更换教室 所耗费的最小体力值。
计算顺序也很好判断,直接从1到n递推即可。对于 i 时间段,它的 f 值只与上个时间段有关。
对于f值的转移,本来我写了一大段文字,但因实在冗长,故将其删去。还是画图比较清晰。
设原课程为a[i],另一课程为b[i],换课成功概率为k[i]。
当 i 时间不申请换课,该时间的课程不变,为a[i]。该状态f[i][j][0]可由两个状态转移而来,一种是上个时间不申请,则上个节点一定为a[i-1]。
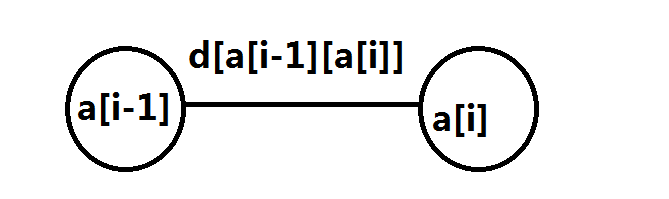
二者所选课程的概率都为1,乘以d[a[i-1]][a[i]]即为期望体力。
若上个位置申请,则其有两种可能,一种失败,期望体力为 概率k[i-1]*路程d[a[i-1]][a[i]],一种成功,期望体力为概率1-k[i-1]*路程d[b[i-1]][a][i]]。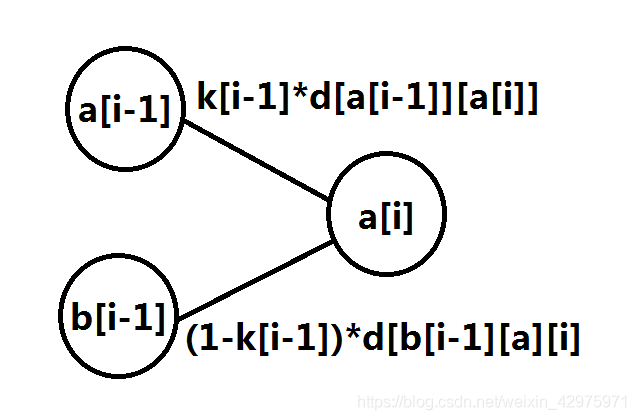
若 i 时间申请更换课程,同样由两种状态更新而来。
一种是上个时间不申请。
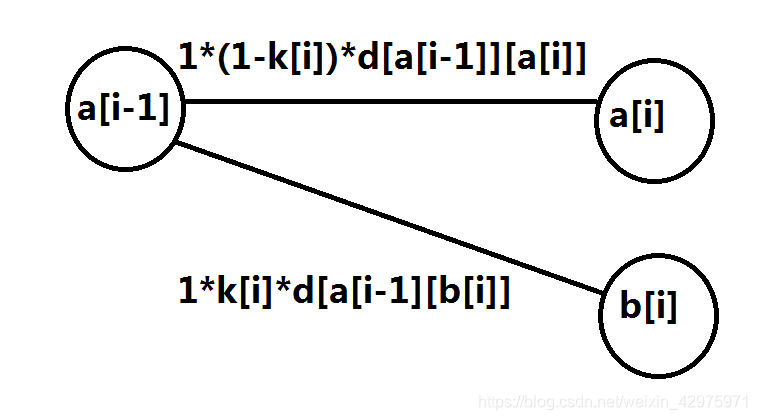
一种是上个时间申请。这种情况要计算两个时间各自申请与否共四种情况分别的概率乘以路程。

(话说我这图怎么越画越小了?)
刚开始做时,我只考虑了当前时间 i 的概率。但实际上申请换课的一个状态f[i][j][1]所表示的课程是不固定的,有成功和不成功两种可能,所以要分别计算概率。
#include组合数问题
开始以为每次 t 都要给定一个不同的 k ,没想出来。后来才看清 k 原来是不变的……话说我这不仔细读题的毛病该改改了。
数据范围2000*2000的组合数可直接爆算,组合数 f[i][j]=f[i-1][j-1]+f[i-1][j],若直接算组合数肯定会爆long long。想一想,以往数值过大我们怎么办?取模!
如何判断它为 k 的倍数?算组合数时对 k 取模,若该组合数取模后数值为0,则表明它为k的倍数,加入答案。
因为求的是所有0<=i<=n,0<=j<=min(i,m)有多少对(i , j)满足C(i , j)是 k 的倍数,即为(n,m)位置的左上方区域的答案总和。容易想到用二维前缀和维护答案。
#include蚯蚓
85分:模拟题意,容易想到用优先队列,每次取队首计算放回即可。
关于切断最长蚯蚓所得的两段,我居然没想到怎么处理乘以 p 的比例问题?因为不能直接每秒改变队内元素的值,所以要用一个sig记录共同生长的大小,取出队首时要先加上sig再乘以p。切得的两段放回队列时要与其他元素保持一致,所以要减去sig,同时还因为这一秒内这两条蚯蚓没有生长,还要减去一个q。
#include100分:关键点——发现此题中隐含的单调性。
85分算法超时主要是因为优先队列有一个log的复杂度,可不可以去掉这个log呢?
我们发现,对于两个蚯蚓 a、b ,设 a 先于 b 被剪断,它们按比例 p 剪得的两只蚯蚓长度 a1、a2;b1、b2(设 a1=a*p,a2=a-a1;b1、b2相同)有这样的大小关系:
a1>b1、a2>b2
首先我们知道,a 先于 b被剪断,则 a 长度必然大于 b,而按比例切断后的 a1、a2,b1、b2 也相应地有着这样的大小关系。而又因为 a1、a2 比 b1、b2 先被切出来,它们每秒钟各自生长一定长度 q ,期间 b 也在生长同样的长度 q ,但在乘上比例 p 之后我们发现b1、b2的生长速度为qp,q(1-p),其实是小于a1、a2的生长速度 q 的(建议手玩一下过程)。所以可得a1>b1、a2>b2。
由于a1、b1、c1……;a2、b2、c2……这两部分按相同比例切出的蚯蚓长度是单调的,故可直接用两个普通队列分别保存。为什么要用两个队列?因为它们二者混合比较后的的长度是不单调的,如,第一次a1最长,将其取出队列后切断。之后的b1、a2之间的长度关系就不确定了,所以要分别存储。
再加上原来还未被切过的蚯蚓,共三个队列,每次询问时将三个队列的队首都取出来比较取最大值即可。
#include愤怒的小鸟
第一种做法:状压dp
f[i] 表示已被射中的猪表示为二进制下的 i 时所需的最少发射次数。
提前预处理出数组 l[i][j] ,二进制下表示这条经过 i、j 号猪的抛物线经过的所有猪。
每次从一个标号最小的且未被击中过的猪进行转移,因为这个猪迟早都要被打,不如提前打掉,否则后面会重复计算状态。
#include第二种做法:搜索
搜索的三个参数:cur 表示枚举到了第cur个猪,cnt 表示有多少条落单的猪不在抛物线上,sum 表示发射了几次鸟,即有 sum 条已有的抛物线。
搜索每只猪,对于该猪有三种情况:
- 可被先前发射的鸟形成的抛物线直接打掉。若符合这种情况则跳过搜索其他两种可能。
- 与先前落单的猪被一起打掉,即组成一条新的抛物线,可供击打后面的猪。
- 落单,不与任何抛物线或其它猪组合。
剪枝:由于落单的猪已经选择互不组合,所以要打掉它们必须另外发射 cnt 次,再加上已有的抛物线数 sum 即为当前情况下的最小答案。若当前的最小答案已经大于之前已求得的答案,直接退出。即 if(sum+cnt>=ans) return;
一个细节,在求抛物线时若系数 a 大于等于零则直接跳过。两只猪的横坐标相同时也要特判并跳过。为避免精度误差,定义eps=1e-8来判断差值。
#include