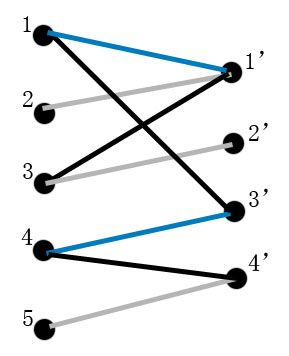
二分图匹配——最大匹配(匈牙利算法),完美匹配(最大权值匹配,KM算法)
最近看了二分图的两个算法,写了一下相关的题,基本都是直接套模板,所以模板很重要,思想搞清楚后,记模板吧。
1.匈牙利算法
匈牙利算法的基本原理如下:
①置M为空;
②找到一条增广路径P,通过异或操作获得更大的匹配M’代替M;
③重复②直到找不到新的增广路径。
增广路径的定义如下:
若P是图G中一条联通两个未匹配顶点的路径,且属于M的边和不属于M的边在P上交替出现,则称P为相对于M的一条增广路径。
①初始状态
当前已有边(1,1’)和(4,3’)属于M。
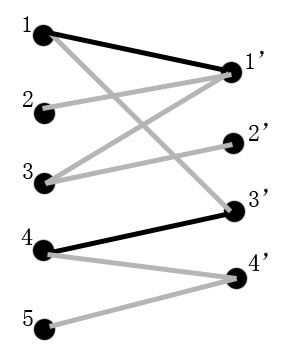
②找到一条增广路径P
如图,增广路径P为:(3 - 1’ - 1 - 3’ - 4 - 4’)。其中,不属于M的路径有:(3, 1’)、(1, 3’)和(4, 4’),属于M的路径有(1‘, 1)和(3’, 4)。显然,在上面的路径P中,不属于M的路径和属于M的路径是交替出现的。[3-1’(蓝), 1’-1(黑), 1-3’(蓝), 3’-4(黑), 4-4’(蓝)]
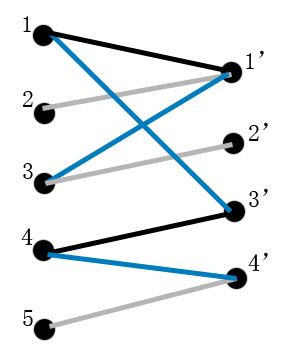
③对第②步中的图进行取反,将原来属于M的路径去除,将原来不属于M的路径加入M中。(即蓝色的边变成黑色,黑色的边变成蓝色)
④完成。
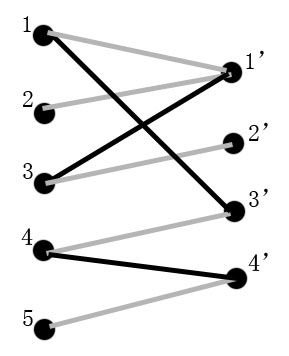
最后再看一下由增广路径的定义可以推出的三个结论:
①P的路径长度必定为奇数,第一条边和最后一条边都不属于M
②P经过取反操作可以得到一个更大的匹配M
③M为G的最大匹配当且仅当不存在相对于M的增广路径
以上作者:睿睿哥
来源:CSDN
原文:https://blog.csdn.net/reid_zhang1993/article/details/44080167
来个题目
http://acm.hdu.edu.cn/showproblem.php?pid=1083
Consider a group of N students and P courses. Each student visits zero, one or more than one courses. Your task is to determine whether it is possible to form a committee of exactly P students that satisfies simultaneously the conditions:
. every student in the committee represents a different course (a student can represent a course if he/she visits that course)
each course has a representative in the committee
Your program should read sets of data from a text file. The first line of the input file contains the number of the data sets. Each data set is presented in the following format:
P N
Count1 Student1 1 Student1 2 … Student1 Count1
Count2 Student2 1 Student2 2 … Student2 Count2
…
CountP StudentP 1 StudentP 2 … StudentP CountP
The first line in each data set contains two positive integers separated by one blank: P (1 <= P <= 100) - the number of courses and N (1 <= N <= 300) - the number of students. The next P lines describe in sequence of the courses . from course 1 to course P, each line describing a course. The description of course i is a line that starts with an integer Count i (0 <= Count i <= N) representing the number of students visiting course i. Next, after a blank, you’ll find the Count i students, visiting the course, each two consecutive separated by one blank. Students are numbered with the positive integers from 1 to N.
There are no blank lines between consecutive sets of data. Input data are correct.
The result of the program is on the standard output. For each input data set the program prints on a single line “YES” if it is possible to form a committee and “NO” otherwise. There should not be any leading blanks at the start of the line.
An example of program input and output:
Sample Input
2
3 3
3 1 2 3
2 1 2
1 1
3 3
2 1 3
2 1 3
1 1
Sample Output
YES
NO
翻译:
考虑一组N学生和P课程。每个学生访问零,一个或多个课程。您的任务是确定是否有可能组建一个完全符合P学生的委员会,同时满足以下条件:
。委员会中的每个学生都代表不同的课程(如果学生访问该课程,学生可以代表课程)
每门课程都有委员会的代表
您的程序应该从文本文件中读取数据集。输入文件的第一行包含数据集的数量。每个数据集以以下格式显示:
P N.
Count1 Student1 1 Student1 2 … Student1 Count1
Count2 Student2 1 Student2 2 … Student2 Count2
…
CountP StudentP 1 StudentP 2 … StudentP CountP
每个数据集中的第一行包含两个由一个空格分隔的正整数:P(1 <= P <= 100) - 课程数和N(1 <= N <= 300) - 学生数。接下来的P行按顺序描述课程。从课程1到课程P,每行描述一门课程。当然,i的描述是以整数Count i(0 <= Count i <= N)开始的行,表示访问课程i的学生的数量。接下来,在空白之后,你会发现Count i学生,参观课程,每两个连续分隔一个空白。学生编号为1到N的正整数。
连续数据集之间没有空行。输入数据是正确的。
程序的结果是标准输出。对于每个输入数据集,如果可以形成委员会,则程序在单行上打印“是”,否则打印“否”。在线的开头不应该有任何前导空白。
程序输入和输出的一个例子:
#include
#include
#include
#include
using namespace std;
const int maxn=1000;
int nx,ny;//记录x,y集合中点的个数
int vis[maxn],cx[maxn],cy[maxn],e[maxn][maxn];//vis标记y中的点有没有被配对
//cx[x]=y,cy[y]=x,表示x,y匹配,即在匹配图中相连
//e[x][y]=1,表示在原二分图中x,y相连
int pr(int x){
for(int y=1;y<=ny;y++){
if(e[x][y]&&!vis[y]){//两个条件:1.x,y相连 2.在本次循环里还没有配对或没有重新配对
vis[y]=1;
if(cy[y]==-1||pr(cy[y])){//两个条件:1、如果此点B从来还没被匹配过(即还没加入过这个匹配圈);
//2、如果此点B被匹配了,但是跟它匹配的点还可以找到其他的点
cx[x]=y;
cy[y]=x;//将x,y匹配
return 1;
}
}
}
return 0;
}
int main(){
int n;
cin>>n;
while(n--){
memset(cx,-1,sizeof(cx));
memset(cy,-1,sizeof(cy));
memset(e,0,sizeof(e));
//初始化cx,cy,e
int m;
cin>>nx>>ny;
for(int x=1;x<=nx;x++){
cin>>m;
while(m--){
int y;
cin>>y;
e[x][y]=1;
}
}
int cnt=0;
for(int x=1;x<=nx;x++){
if(cx[x]==-1){ //如果x还未匹配,进入匹配
memset(vis,0,sizeof(vis));
//初始化标记,此时让y中所有点都未配对
cnt+=pr(x);
}
}
if(cnt==nx){
cout<<"YES"< 2.KM算法
KM算法是用于解决带权二分图的完美匹配的最大匹配值。(你不懂完美匹配,恭喜恭喜),是基于匈牙利算法的。
我惊讶的发现,空说点实在是不好理解(我智商低←_←),所以,下面把问题改成最令人感兴趣的泡妞问题。。。。
一个点集为男生,一个点集为女生,每一个女生对每一个男生有一个好感度(即边权),问如何配对使得最终好感度的和最大。
ex[i][j]表示第i个妹子对第j个男生的好感度。
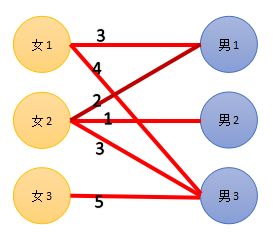
思路
首先这东西为完美匹配,我们先把女生对男生没有好感度的(真可怜)视为好感度为0,那么匹配后自然就是一个完美匹配了!
接下来的问题就是最大匹配值。
每个妹子都期望有个好归宿,所以她们期望能够和自己好感度最高的男生牵手。
对此,我们引入数组exg[i]表示第i个妹子的期望,初始时exg[i]=max(ex[i][j])(即妹子对所有男生中,好感度最高的男生)。
由于现在社会状况为男女比例严重失调,所以男生已经不在乎妹子颜值了,只希望能有一个妹子就好,所以exb[i]表示第i个男生的期望,初始为exb[i]=0;
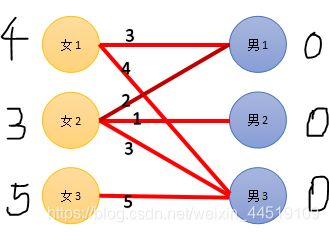
匹配前规定
开始匹配时,每一轮匹配中,每一个男生与女生只能尝试匹配一次!要求为ex[i][j]=exg[i]+exb[j](即双方都要满意对方)
匹配中
第一轮中,女1与男3匹配,成功。
女2与男3匹配,然而男3已经匹配过了,不能匹配,其他男生又不符合要求,这一轮匹配宣告失败。
匹配后
匹配失败后,参与匹配的有女1,女2,男3。
女生中有争执,只好降低自己的期望,女1要想可以匹配其他男生,至少要降低1点期望,女2也同理,所以她们的期望-1,即exg[1]-1,exg[2]-1.
而男3由于得到了妹子的关注,终生大事已经要着落了,自然就开始关注其妹子的颜值了,他的期望就上升1点,即exb[3]+1。
可以发现
1.只有参与匹配的男女才会进行调整。
2.男生上升的期望与女生下降的期望的值是相同的。
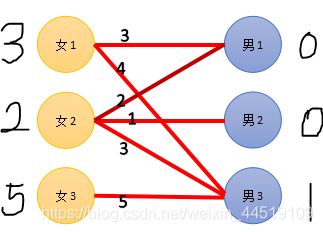
然后重复匹配,失败再进行调整,直到成功。
时间复杂度为O(n 4 ) O(n4)O(n^4)。
优化
设男女生调整的期望值为d
如果朴素的寻找最小d,是要n 2 n2n^2级别的。
对此,我们可以设一个差距数组les[i],表示第i个男生最少要降低多少期望才能达到和一个妹子匹配的要求。一开始les[i]=∞ ∞\infty
当我们匹配一个妹子和男生时,val=exg[i]+exb[j]-ex[i][j],当val=0时说明可以匹配,若val不为0(即val>0),说明男生还差val点期望才能获得这个女生的关注,所以les[j]=min(val,les[j])。
而d就是les中最小的。此时对于没有匹配到的男生,他们离妹子的期待又进了一步,这些男生的les[j]+=d。
时间为O(n)
最终整个算法的复杂度为O(n 3 ) O(n3)
上文作者:LF_本心cy
来源:CSDN
原文:https://blog.csdn.net/Last_Freezen_yue/article/details/68937093
来个题目
http://acm.hdu.edu.cn/showproblem.php?pid=2255
传说在遥远的地方有一个非常富裕的村落,有一天,村长决定进行制度改革:重新分配房子。
这可是一件大事,关系到人民的住房问题啊。村里共有n间房间,刚好有n家老百姓,考虑到每家都要有房住(如果有老百姓没房子住的话,容易引起不安定因素),每家必须分配到一间房子且只能得到一间房子。
另一方面,村长和另外的村领导希望得到最大的效益,这样村里的机构才会有钱.由于老百姓都比较富裕,他们都能对每一间房子在他们的经济范围内出一定的价格,比如有3间房子,一家老百姓可以对第一间出10万,对第2间出2万,对第3间出20万.(当然是在他们的经济范围内).现在这个问题就是村领导怎样分配房子才能使收入最大.(村民即使有钱购买一间房子但不一定能买到,要看村领导分配的).
Input
输入数据包含多组测试用例,每组数据的第一行输入n,表示房子的数量(也是老百姓家的数量),接下来有n行,每行n个数表示第i个村名对第j间房出的价格(n<=300)。
Output
请对每组数据输出最大的收入值,每组的输出占一行。
Sample Input
2
100 10
15 23
Sample Output
123
#include
#include
#include
#include
using namespace std;
const int INF=0x3f3f3f3f;
const int maxn=305;
int a[maxn][maxn];//记录每个人对每间房子出的价格
int ex_x[maxn],ex_y[maxn];//x记录人的期望值,y记录房子的期望值
int vis_x[maxn],vis_y[maxn];//用来标记每一轮匹配中用到的人,房子
int link_y[maxn],slack[maxn];//link_y用来记录房子给了谁
//slack用来记录房子卖给人价格最少还需多少
int n;
int dfs(int x){
vis_x[x]=1;
for(int y=0;y