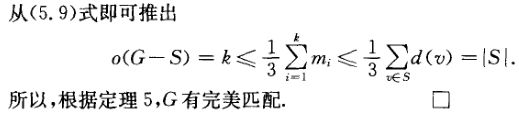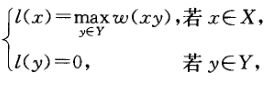《图论及其应用》学习笔记（匹配和因子分解）

匹配：

匹配M：M是E的一个，不包含环的子集，它的任意两条边在G中均不相邻。

M饱和的点v：匹配M的某条边，与顶点v关联。

M非饱和的点v：M中无边与顶点v关联。

完美匹配M：若G中的每个顶点，都是M饱和的点。

最大匹配M：在G中，找不到其它匹配的边数，大于M了。

ps：每个完美匹配，都是最大匹配。

 

M交错路：指图G的边，在E\M和M中交替出现，的路。

M可扩路：起点和终点，都是，非饱和的，M交错路。

ps：这个证明可等价于，M不是最大匹配，当且仅当G含有M可扩路。

充分性证明，M’为M可扩路中，除去M中的边，所组成的边集。在可扩路中，选取的M’内的边集互不相交，因此可算是个匹配。M’有m+1条边，M有m条边。

反之是，必要性证明，M和M’的对称差，意味着去除，M和M’之间公共边。因为M和M’都是匹配，里面的任意两条边均不邻接，因此H中的一个点，不可能同时关联M或M’中的两条边。M’的边多于M的边，H必定存在一个分支，M’的边多于M的边，在这个分支中，也必定存在，以M’中的边开始和结束的路P。

 

偶图的匹配与覆盖：

邻集N(S)：与S的顶点，相邻的所有顶点的集合。

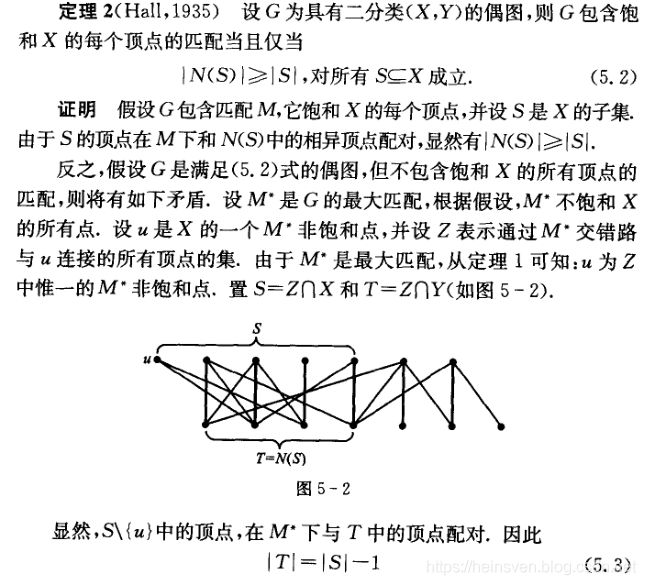
ps：必要性证明，S是X的子集，因此M也饱和S中的每一个顶点，则S中的每个顶点，也匹配于Y中的一个顶点，所以N(S)在原图G中，至少有S。

反之是，充分性证明，为包含所有，含有u点的交错路的顶点集。u肯定是Z中唯一的非饱和点，不然就有可扩路了，不然，在一条交错路上，出现了两个非饱和点，以这两点为端点，截取出来的路，就为可扩路了。

因为T是由Y和连接于u的交错路上的点的交集，所以T中的点所有都是的饱和点。

如果没有交错路的限制，S会和Y中多个点相邻，因此有，。因为Z选取的是，所有连接于u的交错路上的点，所以T必定包含了所有N(S)上的点（如S的某个点到u的某条交错路中，加多一条到N(S)的边，又形成一条交错路）。

因N(S)中每个顶点v，均有一个交错路连接于u，所以v∈Z，但是Z包含了所有T中的点，从而v∈T，这表明，所以有。

 

ps：顶点数X或Y，乘上X或Y上每个点的度数k，则等于边数E(G)。N(S)的点所关联的边数至少为S。

 

覆盖：在顶点集中取个子集K，使得图G的每条边，至少有一个端点在K中。

最小覆盖K：图G不能找到一个覆盖K’，使得。

 

任何匹配M和任何覆盖K，均由。若G是偶图，则有

ps：K至少包含每条边的一个端点。

 

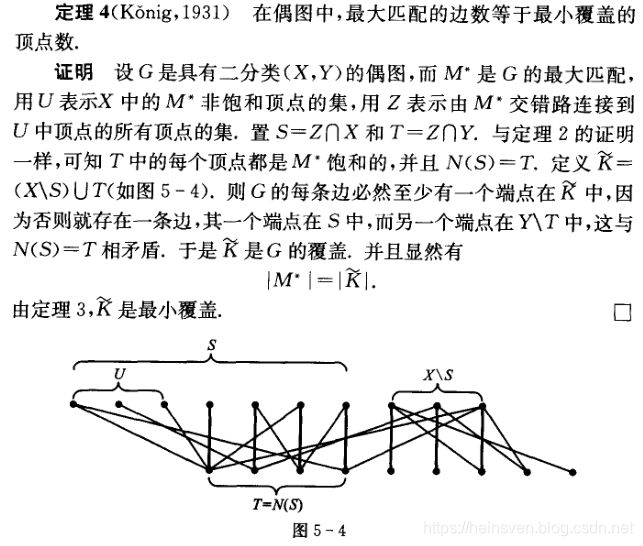
ps：U中的每一个点v，出现在的每一个交错路上，均只有v它一个非饱和点。一个端点在S中，另一个端点也必定在N(S)中，也就是T中，因此和另一个端点在Y\T中，矛盾。由于X\S的点不会和T中的点相连，所以最大匹配里的边，由T与S中的一些饱和点连成的边和包含X\S中的点的匹配边，组成，因此有最大匹配数等于最小覆盖数。

 

Tutte定理与完美匹配：

分支根据，它有奇数个或偶数个顶点，而分成为，奇分支或偶分支。

o(G)：G的奇分支的个数。

 

以下推论是充分条件。例如，有割边的3正则图，不一定就没有，完美匹配。

ps：Gi是奇分支，所以是奇数，因此，奇数乘以奇数，还是奇数，是奇数。又因为奇数减去偶数是奇数，是奇数，它表示原有Gi每个点所关联的边数的2倍，减去Gi先有的边数的两倍，结果为，Gi被S切断的度数，也即边数。有k个mi，且每个mi至少为3，所以有，3k≤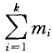。因为S不仅要与Gi这些点连边，而且S内部的点也要连边，因此有：≤。

 

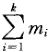因子分解：

图G的一个因子：G的一个生成子图，但至少有一条边。

G的一个因子分解：因子的边的并，且这些因子的边并无交集，即交集为空集。

n-因子：一个n度正则的因子。

n-因子分解：G是几个n-因子的和，且它们的并，就为n-因子分解。

而上述的那个G本身，称为n-可因子化。

 

若G有一个1-因子，即是完美匹配（1-因子是生成子图，且每个点的度都为1），且G为偶阶图（G的度数之和为n=2m）。

所以不能有1-因子，有1-因子。

ps：一个1-因子即为一个完美匹配，即为多个这样的完美匹配构成。因为是完美匹配，中的每个点都要被匹配到，且一个点要有2n-1条边，所以要找出的完美匹配的个数，即1-因子的个数，为2n-1个。可按下述例1的方法来划分。

 

 

例子：

ps：去掉一个完美匹配，则所有顶点的度会减1。在完美匹配中，若割边所关联的顶点选择了其它边，这就不能选择割边了，所以当然会有不含割边的1-因子，因此3-正则图，一定有一个不含割边的1-因子。

 

2-因子分解：

若一个图是2-可因子化，则每个因子，一定是，不相交圈(圈的边无交集)的一个并。（因为这个图的每个2-因子，顶点的度都为2）。

不是2-可因子化的。

若一个2-因子是连通的，则它是一个H圈。（因为这个生成图是连通的，就只有一个圈，也就是H圈。若不是连通的，可能有多个圈）

ps：构造出的n条路，其端点最后连接，形成H圈。

 

2度正则图是一个2-因子。

偶圈能表示为，两个1-因子的和。

例子：

ps：其中的2-因子是一些偶圈，偶圈1-可因子化的，所以这个图也是1-可因子化的。

Peterson图就是个例子，由5边形和5角星形一起构成了，一个2-因子(非连通的生成子图)，和一个联接5边形和5角星的完美匹配。

ps：2-可因子化，意味着，这个连通图是由多个不相交的圈组成。

 

最优匹配与匈牙利算法：

为解决人员分派问题的一个算法。

扎根于u的M交错树：u是非饱和点，树H种的任一点v，有唯一的(u,v)路，是一条M交错路。

匈牙利算法：

ps：表明找不到一个匹配能饱和所有X的顶点，也就是不存在完美匹配。，用路P上的非匹配边，置换掉，路P上的匹配M中的边。

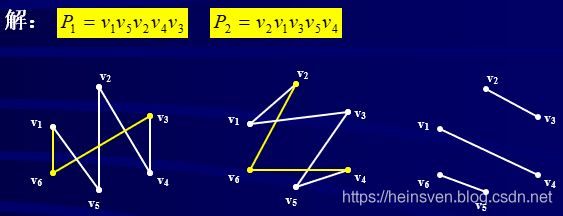
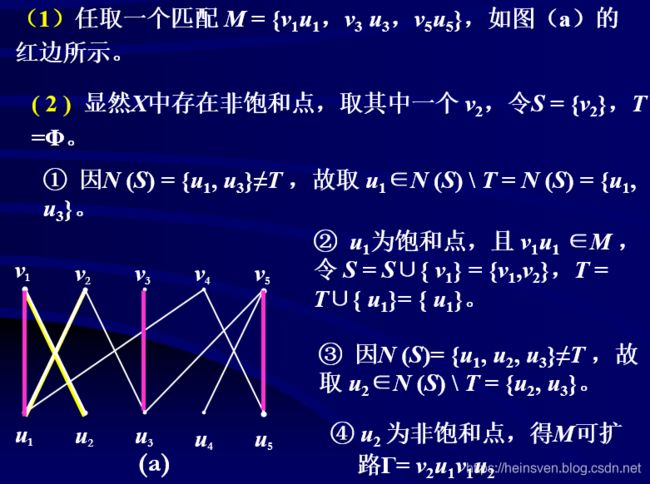
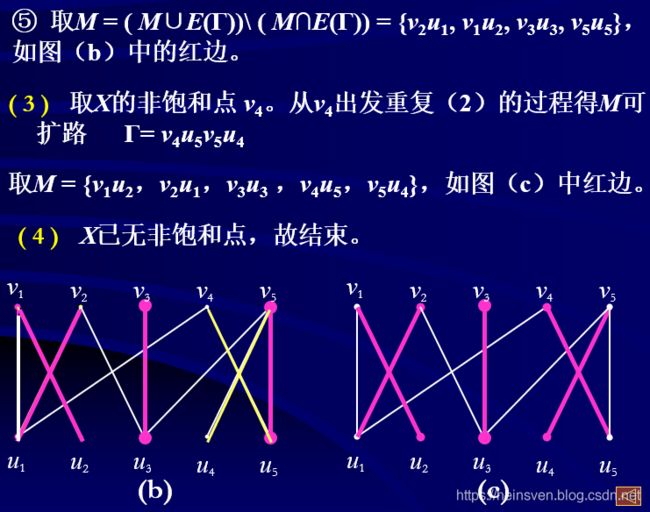
例子：

 

最优匹配：

定义：在赋权图中，寻找一个具有最大权的完美匹配。

对来说，有个不同完美匹配。

可行顶点标号：存在一个实值函数l，使得偶图中，

不管边的权是什么，总存在一个可行顶点标号：

相等子图：具有边集的，G的生成子图。

ps：因为某一对顶点标号之和，总是≥该边的权值，因此所有顶点标号的总和是，图的权值总和的一个上界。是上的完美匹配，因此上的任一两个顶点标号之和都=边上的权值。但在M上取得边，可能会小于，关联的两顶点标号之和。

 

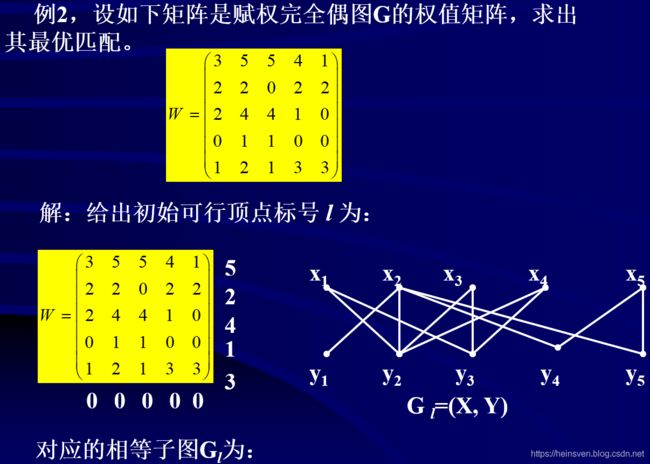
最优匹配算法：

步骤：

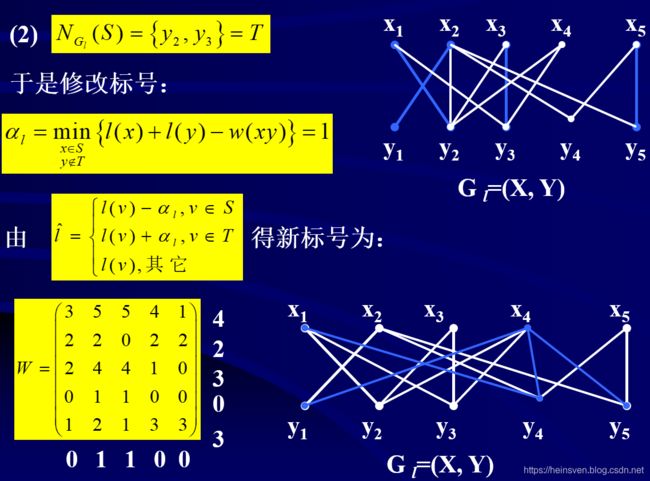
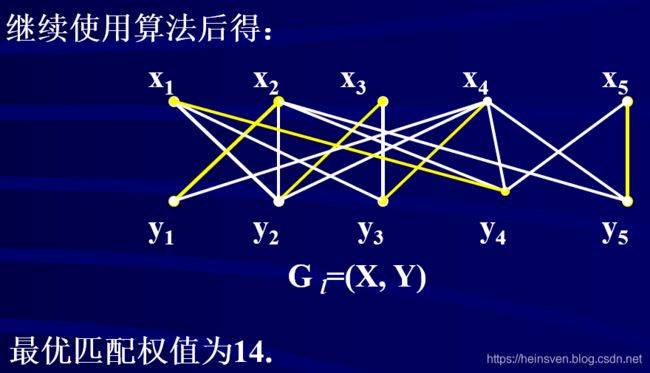
例子：

修改顶点标号方法：

ps：重新计算的α值，涉及到在S集合中，不在T集合中的元素。例如锁定，1、3、4行和1、4、5列。