经典算法题型（一）：排列与组合

• 排列

一、基本概念

排序是常见的数学问题，如何使用编程罗列出所有排序的可能呢？

下面结合leetcode第46题给出简单的分析思路。

二、题目详情

46. 全排列
*给定一个没有重复数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]
输出:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

三、解题分析

如图所示，通过图解分析我们可以看出，只要将排列问题拆解成一个个单独的数字，并对其剩下的数字继续拆分，直到剩下一个数字，就可以得到一种解答。如：[123],取1，得：1->[23],取2，得1->2->3||如果再第二步取3，得1->3->2,以此类推得出所有结果。

四、代码及注释：

package IMUHERO;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
public class Solution46 {
    ArrayList>res=new ArrayList>();
    boolean [] visited;
    public List> permute(int[] nums) {
        if (nums.length==0||nums==null)return res;
        LinkedListlist=new LinkedList();
        visited=new boolean[nums.length];//初始值为false；
        generatePermute(nums,0,list);
        return res;
    }
    public void generatePermute(int [] nums,int index,LinkedList p){
        if (index==nums.length){
            res.add((LinkedList)p.clone());//注意此处不能直接add(p),这样会相当于添加了一个引用，后期随着p的回溯修改，结果中的值也会随之被修改，不是我们想要的结果
            return;
        }
        for (int i=0;i

• 组合

一、基本概念

组合与排列不同的是，他不在意前后顺序，而只在意包含的内容

比如上题组合中的123和132、213等，在组合中都是同一种结果 。

下面结合leetcode第77题给出简单的分析思路。

二、题目

77. 组合

给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数的组合。

示例:

输入: n = 4, k = 2
输出:
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

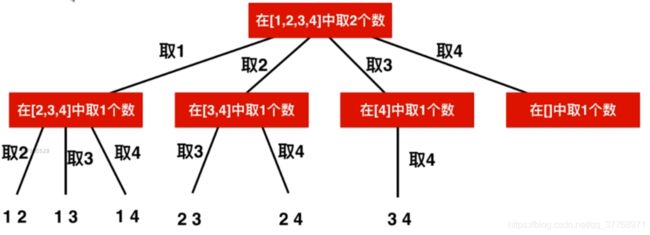
三、分析

 从图中可以看出，如果在前一次已经取出的数字，将不会在后面的数字组合中出现，从而有效避免重复。

四、代码及注释

package IMUHERO;

import java.util.LinkedList;
import java.util.List;

public class Solution77 {
    LinkedList>res=new LinkedList<>();
    public List> combine(int n, int k) {
        if (n==0||k==0)return res;
        LinkedListlist=new LinkedList<>();
        generateCombine(n,k,1,list);
        return res;
    }
    public void generateCombine(int n, int k, int start, LinkedListlist){
        //与排序不同的是，递归参数中含有一个start，用来标记当前遍历到第几个数字，之前遍历完的将不在访问，此操作在下面的for循环中体现
        if (list.size()==k){
            res.addLast((LinkedList)list.clone());
            return;
        }
        //for (int i=start;i<=n;i++),下面进行剪枝
        // 还有k - list.size()个空位, 所以, [i...n] 中至少要有 k - list.size() 个元素
        // i最多为 n - (k - list.size()) + 1
        for (int i=start;i<= n - (k - list.size()) + 1;i++){
            list.addLast(i);
            generateCombine(n,k,i+1,list);
            list.removeLast();
        }
        return;
    }
}

->>此处有一个优化剪枝操作，大概可以提升10%的性能，主要目的是为了避免无效多余的递归操作。

剪枝也是递归操作中非常常用的优化方式。