Wagner Fischer算法（字符串编辑距离，Edit Distance）

字符串编辑距离裸题

题目描述 ：点击转到网址

设A和B是两个字符串。我们要用最少的字符操作次数，将字符串A转换为字符串B。这里所说的字符操作共有三种： 

1. 删除一个字符； 
2. 插入一个字符； 
3. 将一个字符改为另一个字符。 
对任给的两个字符串A和B，计算出将字符串A变换为字符串B所用的最少字符操作次数。

输入

第一行为字符串A；第二行为字符串B；字符串A和B的长度均小于200。

输出

只有一个正整数，为最少字符操作次数。

样例输入 Copy

sfdxbqw
gfdgw

样例输出 Copy

4

字符串a,b的长度分别是m,n:

定义dp[ i ] [ j ] :字符串a的前 i 个字符构成的前缀与字符串b的前 j 个字符串构成的前缀之间的编辑距离:

这里举个例子：a = "math"  b = "mouth";

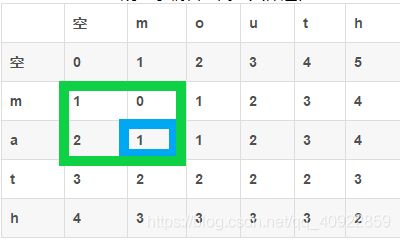
下面说明一下这个表是怎么看的：

 

动态规划求编辑距离的具体过程

	空	m	o	u	t	h
空	0	1	2	3	4	5
m	1	0	1	2	3	4
a	2	1	1	2	3	4
t	3	2	2	2	2	3
h	4	3	3	3	3	2

表中的数值对应dp[ i ][ j ];

 

首先是那两个“空”，就是两个字符串从空串开始求。第一行的“0,1,2,3,4,5,6” 对应dp[0][j] , 意思就是，从a是空”字符串到从b是“空”，“m”,"mo","mou","mout","mouth"的编辑距离是，0,1,2,3,4,5,6。左边第一例的“0,1,2,3,4”也是一样。

下面来看中间的部分：

在匹配a[i],与b[j]的过程中：

如果a[ i ]==b[ j ] ,那么就不需要编辑，从a[i-1],b[i-1]对应的状态转移过来就行；

这时候：dp[ i ][ j ]=dp[ i- 1][ j -1 ];

如果a[ i ] != b[ j ] ,那么我们就考虑从a[ i ],b[ j-1]; a[ i-1 ] ,b[ j ] ,a[ i-1],b[ j-1 ]对应的状态去转移到a[ i ],b[ j ]对应的状态，因为这三个状态再经过一次操作op，再去完成二者变成相等，和a[ i ],b[ j ]对应的状态直接去进行变成相等，得到的结果是一样的，编辑距离要求的是最终两个完整字符串操作次数最少而达到相等，所以我们必须从这三种状态里选择数值最小的那个。

这时候：dp[ i ][ j ]=min(dp[ i ][ j-1],dp[ i-1][ j-1],dp[ i-1][ j-1]) + 1;       // :加的这个1就是那个操作op

#include
#include
#include
using namespace std;
int dp[220][220];  //n较小，可以用这样
int main(){
    string a,b;
    cin>>a>>b;
    int m=a.length();
    int n=b.length();
    dp[0][0]=0;
    for(int j=1;j<=n;j++){
        dp[0][j]=j;  //填充边界
    }
    for(int i=1;i<=m;i++){
        dp[i][0]=i;  //填充边界
        for(int j=1;j<=n;j++){
            if(a[i-1]==b[j-1]){   //注意下标哈
                dp[i][j]=dp[i-1][j-1];
            }
            else{
                dp[i][j]=min(min(dp[i][j-1],dp[i-1][j]),dp[i-1][j-1])+1;
            }
        } 
    }
    cout<

滚动数组优化（字符串长度10000+，这时候开二位数组会爆掉，改用两个1000000大小的来回滚动使用，节约空间）：

#include
#include
#include
#include
using namespace std;
int dp1[100000];
int dp2[100000];
int main(){
    string a,b;
    cin>>a>>b;
    if(a.length()>b.length()){   //保证b是长的那个
        swap(a,b);
    }
    int m=a.length();
    int n=b.length();
    for(int j=0;j<=n;j++){
        dp2[j]=j;
    }
    for(int i=1;i<=m;i++){
        dp1[0]=i;
        for(int j=1;j<=n;j++){
            if(a[i-1]==b[j-1]){
                dp1[j]=dp2[j-1];
            }
            else {
                dp1[j]=min(min(dp2[j],dp2[j-1]),dp1[j-1])+1;
            }
        }
        swap(dp1,dp2);
    }
    if(a.length()==b.length())
        cout<