算法导论------------计数排序and基数排序

    计数排序假设n个输入元素中的每一个都介于0和k之间的整数，k为n个数中最大的元素。当k=O(n)时，计数排序的运行时间为θ(n)。计数排序的基本思想是：对n个输入元素中每一个元素x，统计出小于等于x的元素个数，根据x的个数可以确定x在输出数组中的最终位置。此过程需要引入两个辅助存放空间，存放结果的B[1...n]，用于确定每个元素个数的数组C[0...k]。算法的具体步骤如下：

（1）根据输入数组A中元素的值确定k的值，并初始化C[1....k]= 0；

（2）遍历输入数组A中的元素，确定每个元素的出现的次数，并将A中第i个元素出现的次数存放在C[A[i]]中，然后C[i]=C[i]+C[i-1]，在C中确定A中每个元素前面有多个元素；

（3）逆序遍历数组A中的元素，在C中查找A中出现的次数，并结果数组B中确定其位置，然后将其在C中对应的次数减少1。

#include
using namespace std;

void count_sort(int a[], int b[], int k, int length)
{
	int i, j;
	//each element in A between 0 and k [0,k],total k+1 elements;
	// int *c = new int[k + 1];
	int *c = (int*)malloc(sizeof(int)*(k+1));
	memset(c, 0, (k+1)*sizeof(int));

	//c[i] now contains the number of element equal to i;
	for (i = 0; i < length; ++i)
		c[a[i]] = c[a[i]] + 1;

	//c[i] now contains the number of elements less than or equal to i;
	for (j = 1; j <= k; ++j)
		c[j] = c[j] + c[j - 1];

	for (i = length - 1; i >= 0; i--)
	{
		b[c[a[i]] - 1] = a[i];
		c[a[i]] = c[a[i]] - 1;
	}//a[i]表示输入的元素，c[a[i]]表示出现的次数，那么b[c[a[i]] - 1]表示a[i]放到b数组中的位置
	//放入之后，那么c[a[i]]的次数应该减少
}

int main()
{
	int a[] = { 5, 6, 9, 5, 0, 8, 2, 1, 6, 9, 8, 3, 4, 8, 6, 7, 6, 3, 3, 3, 3, 3, 8, 8, 8,11 };
	int len = sizeof(a) / sizeof(int);
	cout << len << endl;

	int b[26];
	count_sort(a, b, 11, len);

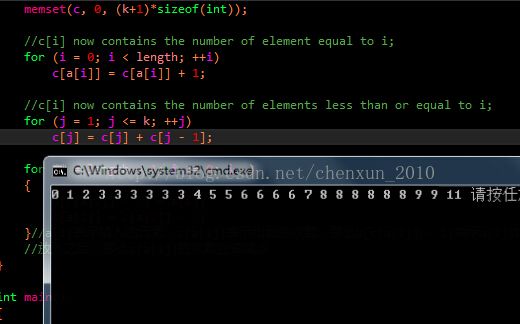
	for (int i = 0; i < len;i++)
		cout << b[i] << " ";
}

（2）基于计数排序的 基数排序：基数排序用到基数排序

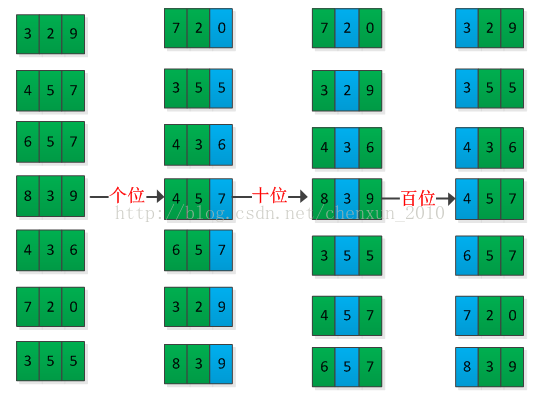
基数排序排序过程无须比较关键字，而是通过“分配”和“收集”过程来实现排序，它的时间复杂度可达到线性阶：O(n)。对于十进制数来说，每一位的在[0,9]之中，d位的数，则有d列。基数排序首先按低位有效数字进行排序，然后逐次向上一位进行排序，直到最高位排序结束。举例说明基数排序过程，如下图所示：

        

基数排序算法很直观，假设长度为n的数组A中，每个元素都有d位数字，其中第1位是最低位，第d位是最高位。书中给出了伪代码如下所示：

引理：给定n个d位数，每一个数位可以取k种可能值。如果所用的稳定排序需要θ(n+k)的时间，基数排序算法性能以θ(d(n+k))的时间正确对这些数进行排序。
为了完整的理解基数排序，结合上面的计数排序，采用C语言实现一个程序，运用计数排序算法对一组3位数进行排序，程序如下：

#include

using namespace std;

int get_digit_num(int data)
{
	int size=0;
	while (data)
	{
		size++;
		data = data / 10;
		
	}

	return size;
}


int get_digit(int data, int size)
{
	int tmp;
	tmp= data;
	while (size)
	{
		tmp = tmp / 10;
		size--;
	}

	return (tmp % 10);
}

void radix_sort(int *datas, int len, int size)
{
	int i, j, k;


	int *num = (int*)malloc(len * sizeof(int));
	int *counts = (int*)malloc(len * sizeof(int));
	int *save = (int*)malloc(len * sizeof(int));


	//memset(temps, 0, 10 * sizeof(int));
	//memset(tmpd, -1, 10 * sizeof(int));
	//memset(rets, -1, 10 * sizeof(int));


	for (i = 0; i < size; i++)
	{	
		memset(num, 0, len * sizeof(int));
		memset(counts, 0, len * sizeof(int));
		memset(save, 0, len * sizeof(int));

		for (j = 0; j < len; j++)
			num[j] = get_digit(datas[j], i);

		for (j = 0; j < len; j++)
			counts[num[j]] = counts[num[j]] + 1;

		for (k = 1; k < 10; k++)
			counts[k] = counts[k] + counts[k - 1];

		for (j = len - 1; j >= 0; j--)
		{
			save[counts[num[j]] - 1] = datas[j];
			counts[num[j]] = counts[num[j]] - 1;
		}

		memcpy(datas, save, sizeof(int)*len);

	} 

	free(num);
	free(counts);
	free(save);
}

int max(int *datas, size_t length)
{
	int k = datas[0];
	int i;
	for (i = 1; i k)aaa
		k = datas[i];
	return k;
}


int main()
{
	int i;
	int datas[] = { 1, 11, 99, 55, 432, 578, 256, 782, 691, 206, 942, 387, 696, 374, 123, 55556, 888888888 };
	int len = sizeof(datas) / sizeof(int);
	int k = max(datas, len);
	int size = get_digit_num(k);
	radix_sort(datas, len, size);
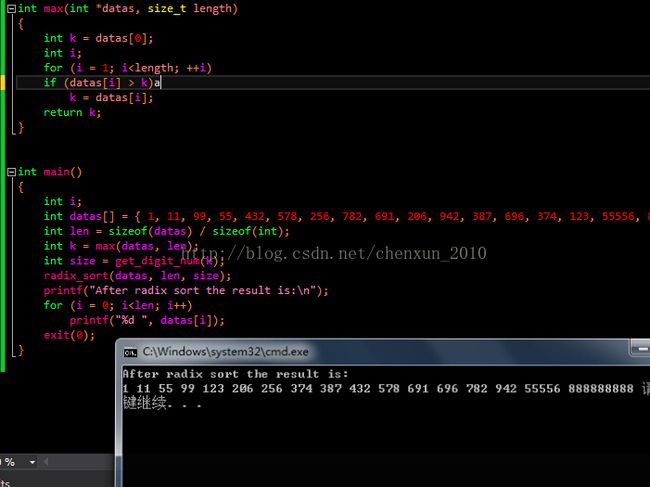
	printf("After radix sort the result is:\n");
	for (i = 0; i